本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记，详细视频参考
【电子科技大学】离散数学（上） 王丽杰
【电子科技大学】离散数学（下） 王丽杰
latex的离散数学写法参考： 离散数学与组合数学-01

离散数学公式
!符号 代码 含义
$\wedge$ \wedge 且
$\vee$ \vee 或
$\cap$ \cap 交
$\cup$ \cup 并
$\subseteq$ \subseteq 子集
$⊈$ \nsubseteq 不是子集
$\subset$ \subset 真子集
$\not\subset$ \not\subset 不是真子集
$\in$ \in 属于
$\notin$ \not\in 不属于
$\leftrightarrow$ \leftrightarrow 等价
$\iff$ \Leftrightarrow 等值
$\neg$ \neg或\lnot 非
$\mathbb{R}$ \mathbb{R} 实数集
$\mathbb{Z}$ \mathbb{Z} 整数集
$\varnothing$ \varnothing 空集
$\forall$ \forall 对任意的
$\exists$ \exists 存在
$\ge$ \geq大于等于
$\le$ \leq 小于等于

1.离散数学与组合数学-01集合论

1.1 集合定义

1.1.1 什么是集合

1. A set is a group of objects. (simplest way)
2. By a set we mean any collection M into a whole of definite distinct objects m (which
   we called elements of M) of our perception or of our thought. (Cantor’s way)
3. 集合 是由指定范围内的满足给定条件的所有对象聚集在一起构成，每一个对象称
   为这个集合的元素。(In chinese)
4. 外延公理 + 空集存在公理 + 无序对公理 + 并集公理 + 幂集公理 + 无穷公理 +
   替换公理 + 正则公理 + 选择公理。(ZFC 公理化集合论):引入ZFC公理化的原因是避免出现悖论的集合，如我给小镇里不自己理发的人理发。

1.1.2 集合案例

1 所有英文字母
2 所有小于 100 的正奇数
3 中国所有的残疾人
4 世界上所有的数学家
5 某植物园的所有植物
6 天安门广场所有的路灯和树

1.1.3 集合的符号表示

N代表自然数集（非负整数集）,而N*则表示正整数集,英文是natural number
Z表示整数集,来自于德语,德语中的整数叫做Zahlen
Q表示的是有理数集,由于两个数之比(商)叫做有理数,商的英文是quotient,所以用Q来表示
R表示集合理论中的实数集,而复数中的实数部分也以此符号为代表,英文是real numbe

1.2 集合表示

1.2.1属于关系

\alpha \in A
$\alpha \in A$

1.2.2 枚举法

A = { a , b , c , d } A = \left\{a,b,c,d \right\} A={a,b,c,d}

1.2.3 叙述法

A = \left\{x|x \in Z,x < 10 \right\}
A = { x ∣ x ∈ Z , x < 10 } A = \left\{x|x \in Z,x < 10 \right\} A={x∣x∈Z,x<10}

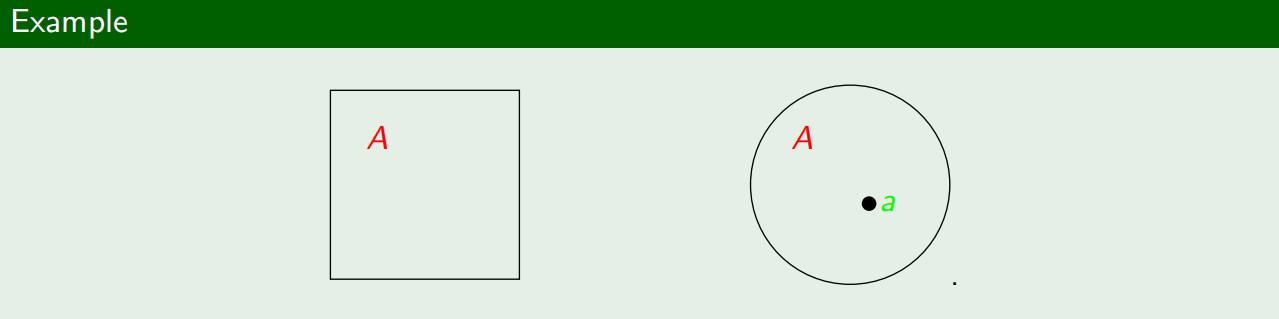
1.2.4 文氏图

文氏图是利用平面上的点来做成对集合的图解方法。一般使用平面上的方形或圆形表示一个集合，而使用平面上的一个小圆点来表示集合的元素。

1.3 集合基数

1.3.1 什么是集合基数

集合 A 中的元素个数称为集合的基数(base number)，记为 |A|
若一个集合的基数是有限的，称该集合为有限集(finite set)
若一个集合的基数是无限的，称该集合为无限集(infinite set)

1.3.2 集合基数案例

A = {a, b, c}, |A| = 3
B ={a, {b, c}},|B| = 2

1.4 集合间关系

1.4.1 空集

\varnothing
不含任何元素的集合叫做空集(empty set)，记作 $\varnothing$.
空集可以符号化为 ∅ = { x ∣ x ≠ x } \varnothing =\left\{x|x \neq x \right\} ∅={x∣x=x}.

1.4.2 全集

针对一个具体范围，我们考虑的所有对象的集合叫做全集(universal set)，记作 U 或 E.在文氏图一般使用方形表示全集。

1.4.3 集合的相等关系

1.4.4 包含关系

子集和真子集

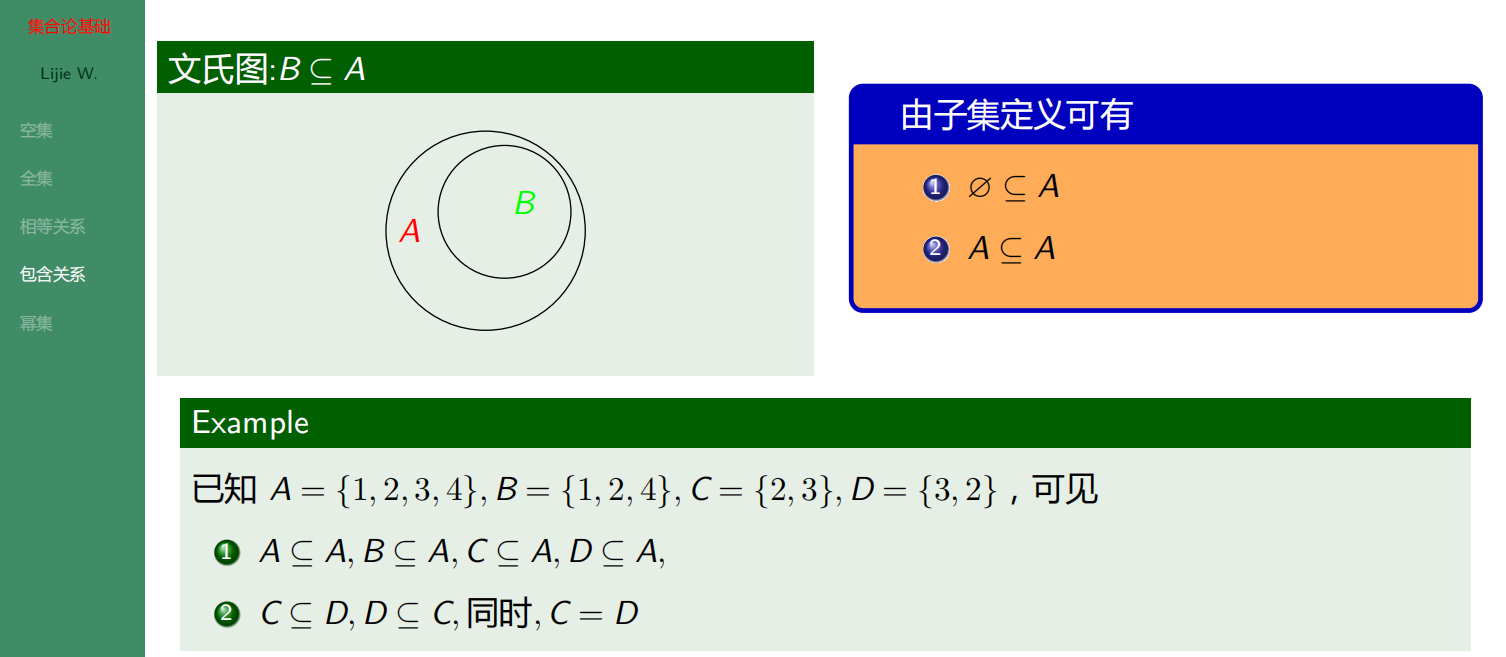
证明集合相等 重点

设 A, B 为任意两个集合，则 A = B ⇔ A ⊆ B 并且 B ⊆ A

n 元集的子集

1.4.5 幂集

1.5 集合的基本运算

1.5.1 并集

1.5.2 交集

1.5.3 补集

1.5.4 差集

1.5.5 对称差集

1.5.6 并集和交集的扩展

1.6 运算定律及其证明

1.6.1 运算定理

幂等率说明：$A\cup A=A$ 类似 1的n次幂等于1
结合律(associative laws)说明：在数学中，结合律(associative laws)是二元运算可以有的一个性质，意指在一个包含有二个以上的可结合运算子的表示式，只要算子的位置没有改变，其运算的顺序就不会对运算出来的值有影响
同一率说明: $A\cup \varnothing =A,A\cap U=A$ 。同一率又称为幺律，这是因为 如果存在一个元b,对任意元x，均有bx=xb=x,则称b为幺元
零率说明: $A\cap \varnothing =\varnothing ,A\cup U=U$ 。零率又称为幺律，这是因为 在抽象代数中，如果存在一个元a,对任意元x，均有ax=xa=a,则称a为零元
德摩根率：非(P 且 Q) = (非 P) 或 (非 Q) ，非(P 或 Q) = (非 P) 且 (非 Q)
分配率的文氏图说明：

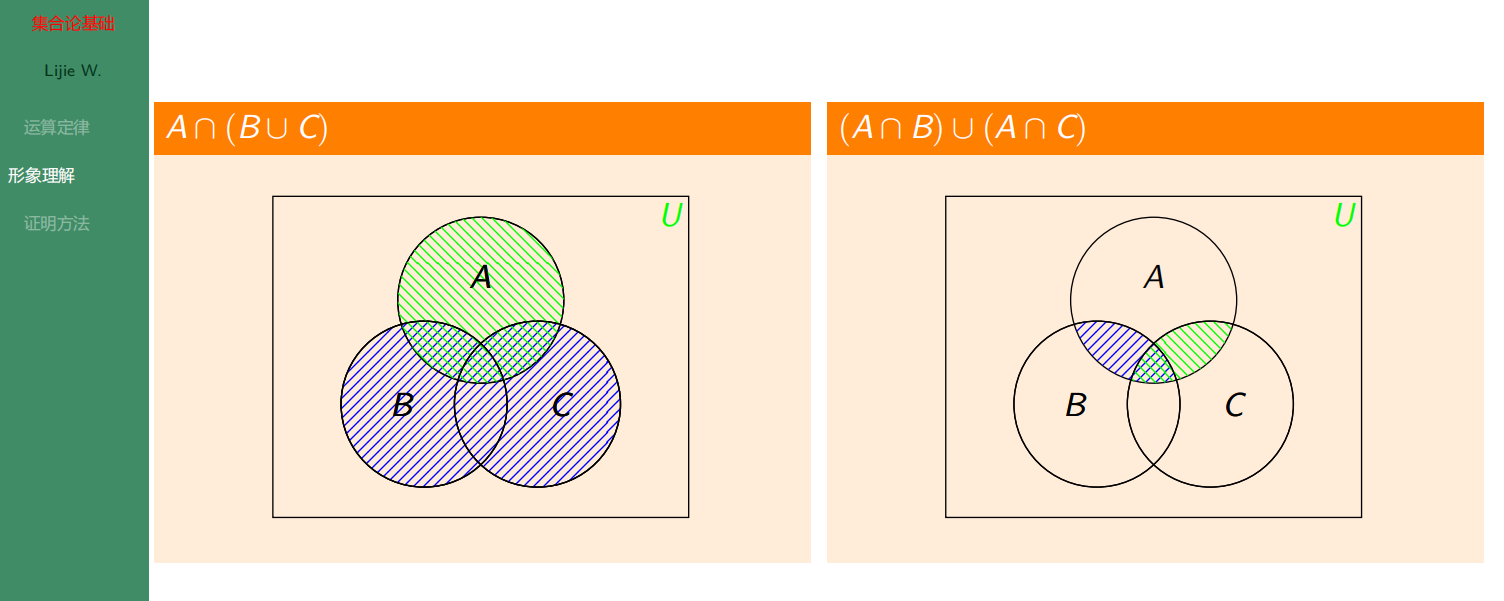
1.6.2 证明

证明方法

德摩根律证明

1.7 可数集合与不可数集合

1.7.1 自然数集的定义

定义 (皮亚诺公理)

定义 (冯 • 诺依曼的自然数定义)

1.7.2 如何比较集合的大小？

等势

1.7.3 可数集合

可数集合定义

正奇数集合 O + 与素数集合 P

有理数集合 Q

从有限到无限，不仅仅是简单数量上的变化 (量变)，而引起了本质的改变 (质变)。
两个无限集合的“大小”已经不能单纯使用集合中的元素个数来衡量。ℵ0
表示一切可数集合的基数，是一种抽象的表达。
表面上个数完全不相等的两个集合之间仍可能存在等势关系，如集合与其真子集之间，这体现了有限集合和无限集合的根本差别。

1.7.4 不可数集合