深入解析快速排序算法
- 一、快速排序算法简介
- 二、快速排序算法过程
- 三、快速排序算法示例
- 四、快速排序算法分析
- 1. 时间复杂度:
- 2. 空间复杂度:
- 3. 稳定性:
- 五、快速排序算法优化
- 1. 优化基准元素的选择:
- 2. 优化小数组的排序:
- 3. 尾递归优化:
- 4. 循环展开:
- 五、快速排序算法的应用场景
- 七、快速排序算法的稳定性问题
- 八、总结与展望
在日常生活和计算机应用中,排序是一个常见的操作。无论是整理书架上的书籍,还是将一组数字按从小到大的顺序排列,我们都在进行着排序的操作。在计算机科学中,排序算法更是数据处理的基础。其中,快速排序算法以其高效的性能,在实际应用中备受青睐。本文将详细介绍快速排序算法的原理、过程,并给出伪代码及C语言代码的示例。
一、快速排序算法简介
快速排序算法是由英国计算机科学家C.A.R. Hoare于1960年提出的一种排序算法。它的基本思想是:通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法采用了分治的思想,将一个大的问题划分为几个小的子问题来解决。在快速排序中,这个大问题就是待排序的数组,而子问题则是划分后的两个较小的数组。通过递归地对子问题进行排序,最终得到整个数组的排序结果。
二、快速排序算法过程
快速排序算法的过程可以分为三个步骤:分解、解决和合并。
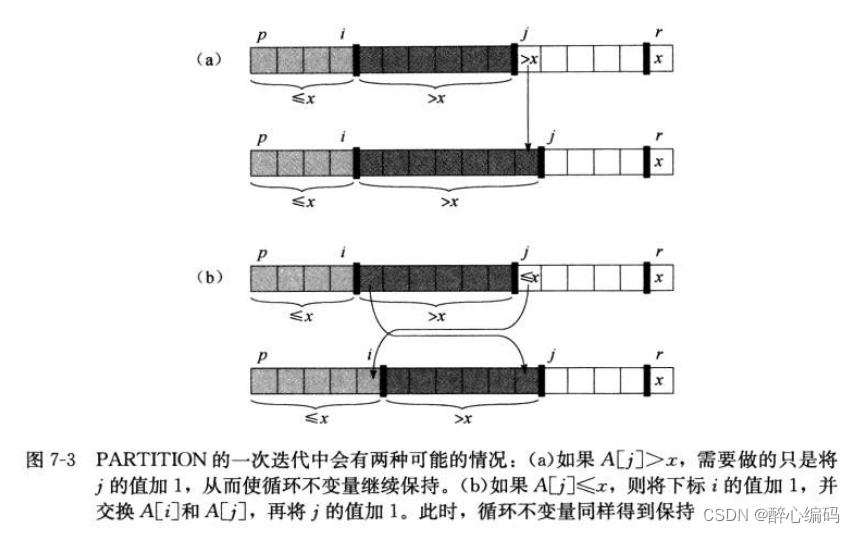
分解:选择一个基准元素(pivot),将数组划分为两个子数组,使得第一个子数组中的所有元素都小于基准元素,而第二个子数组中的所有元素都大于基准元素。这个步骤通常通过一个叫做PARTITION的过程来实现。
解决:递归地对两个子数组进行快速排序。
合并:由于快速排序是原址排序,即在排序过程中不需要额外的存储空间来存放排序结果,因此不需要合并操作。排序完成后,原数组就已经是有序的了。
下面是一个快速排序算法的伪代码实现:
QUICKSORT(A, p, r)
if p < r
q = PARTITION(A, p, r)
QUICKSORT(A, p, q - 1)
QUICKSORT(A, q + 1, r)
PARTITION(A, p, r)
x = A[r]
i = p - 1
for j = p to r - 1
if A[j] <= x
i = i + 1
exchange A[i] with A[j]
exchange A[i + 1] with A[r]
return i + 1
在上面的伪代码中,QUICKSORT函数是快速排序的主函数,它接受一个数组A和两个下标p和r作为参数,表示要对数组A中从下标p到下标r的部分进行排序。PARTITION函数则是用来实现数组的划分操作。它选择一个基准元素(这里选择的是A[r]),然后将数组划分为两个子数组,使得左边的子数组中的所有元素都小于等于基准元素,右边的子数组中的所有元素都大于基准元素。最后返回基准元素在排序后数组中的位置。
三、快速排序算法示例
下面是一个用C语言实现的快速排序算法示例
#include <stdio.h>
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n -1);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
四、快速排序算法分析
1. 时间复杂度:
- 最好情况:每次划分都能得到大致相等的两部分,此时快速排序的时间复杂度为O(n log n)。
- 平均情况:快速排序的平均时间复杂度也是O(n log n)。
- 最坏情况:当输入数组已经有序或逆序时,每次划分只能得到一个子数组,此时快速排序的时间复杂度为O(n²)。为了避免最坏情况的发生,可以采用随机化策略,即随机选择一个元素作为基准元素。
2. 空间复杂度:
- 递归调用栈的深度在最坏情况下为O(n),因此空间复杂度为O(n)。
- 然而,在最好情况下,递归调用栈的深度为O(log n),因此空间复杂度可以降低到O(log n)。如果采用迭代而非递归的方式实现快速排序,可以将空间复杂度降低到O(1)。
3. 稳定性:
- 快速排序算法不是稳定的排序算法。在划分过程中,相等的元素可能会因为交换而改变它们之间的相对顺序。
快速排序算法的性能在很大程度上取决于划分是否平衡。当划分是平衡的(即,基准元素将数组几乎平均地分成两个子数组)时,快速排序的性能接近于最优。然而,如果划分是不平衡的(例如,一个子数组包含大多数元素,而另一个子数组几乎为空),那么性能将接近于最坏情况。
在最坏情况下,快速排序的时间复杂度为O(n²),其中n是待排序数组的长度。这是因为当输入数组已经有序或逆序时,每次划分都会得到一个包含n-1个元素的子数组和一个空子数组,导致算法的性能退化为O(n²)。然而,在平均情况下,快速排序的时间复杂度为O(nlogn),这是因为它可以在平均情况下实现平衡划分。
为了改善最坏情况性能,可以采用一些优化策略,如随机化基准选择(Randomized Pivot Selection)或三数取中法(Median-of-Three)。这些策略有助于减少最坏情况发生的可能性,从而提高算法的整体性能。
五、快速排序算法优化
1. 优化基准元素的选择:
- 可以选择数组中的中位数作为基准元素,而不是简单地选择第一个元素或最后一个元素。这样可以减少划分不平衡的可能性。
- 另一种常见的策略是采用“三数取中”法,即选择数组的第一个元素、中间元素和最后一个元素中的中位数作为基准元素。
2. 优化小数组的排序:
- 对于非常小的子数组(如长度小于10),快速排序可能不是最优的选择。在这种情况下,可以切换到插入排序等简单排序算法来提高效率。
3. 尾递归优化:
- 在某些实现中,可以通过尾递归优化来减少递归调用栈的深度,从而降低空间复杂度。然而,这通常需要更复杂的代码和额外的逻辑判断。
4. 循环展开:
- 在内部循环中展开一些迭代可以减少循环的开销,从而提高算法的执行速度。但这也会增加代码的复杂性和可读性。
随机化基准选择:在选择基准元素时,不总是选择固定位置的元素,而是随机选择一个元素作为基准。这样可以减少输入数据对算法性能的影响,使得算法在平均情况下的性能更加稳定。
三数取中法:在选择基准元素时,选择待排序数组的第一个、最后一个和中间位置的三个元素中的中值作为基准。这种方法可以在一定程度上避免最坏情况的发生,提高算法性能。
插入排序优化:当待排序数组的长度较小(通常设定为小于或等于某个阈值)时,可以采用插入排序作为终止条件。因为插入排序在处理小规模数据时具有较高的效率,这样可以避免快速排序在处理小规模数据时产生的额外开销。
五、快速排序算法的应用场景
快速排序算法由于其高效的性能和易于实现的特性,在实际应用中得到了广泛的应用。它常被用于对大规模数据进行排序,如数据库查询、大数据分析等领域。此外,快速排序算法也可以作为其他算法的基础,如堆排序、归并排序等。
总结来说,快速排序算法是一种高效的排序算法,其性能在很大程度上取决于划分的平衡性。通过采用一些优化策略,我们可以提高快速排序算法的性能和稳定性。在实际应用中,我们可以根据具体需求选择合适的排序算法,除了时间复杂度外,空间复杂度也是评估排序算法性能的重要指标。快速排序算法的空间复杂度主要取决于递归调用的深度。在最好的情况下,每次划分都能得到大致相等的两部分,递归树的深度为O(logn),因此空间复杂度为O(logn)。然而,在最坏的情况下,递归树的深度为n-1,导致空间复杂度为O(n)。在实际应用中,由于栈空间的限制,当处理大规模数据时,最坏情况下的空间复杂度可能导致栈溢出错误。
为了降低空间复杂度,可以采用迭代而非递归的方式实现快速排序。迭代版本的快速排序使用显式的栈来模拟递归过程,从而避免了递归调用栈的开销。这样可以将空间复杂度降低到O(logn)(在最好情况下)或O(n)(在最坏情况下),但由于需要维护额外的栈结构,实现起来相对复杂。
七、快速排序算法的稳定性问题
稳定性是排序算法的一个重要属性,它指的是在排序过程中,相等的元素之间的相对顺序是否保持不变。对于快速排序算法来说,由于它在划分过程中可能会改变相等元素之间的相对顺序,因此它不是一个稳定的排序算法。
在某些应用场景下,稳定性是非常重要的。例如,在处理一组包含姓名和年龄的记录时,我们可能希望先按照年龄进行排序,然后再按照姓名进行排序。在这种情况下,如果使用的排序算法不是稳定的,那么最终的排序结果可能无法满足需求。
为了解决这个问题,可以在快速排序算法的基础上引入额外的机制来保持稳定性。例如,在划分过程中,当遇到相等的元素时,可以根据它们的原始顺序进行排序。这样可以在一定程度上保持稳定性,但会增加算法的实现复杂度和运行时间。
八、总结与展望
本文对快速排序算法进行了深入解析,探讨了其基本思想、实现过程、性能特点以及优化策略。快速排序算法以其高效的性能和易于实现的特性在实际应用中得到了广泛的应用。然而,它也存在一些局限性,如最坏情况下的时间复杂度和空间复杂度较高、不是稳定的排序算法等。
在未来的研究中,可以进一步探索快速排序算法的优化策略和应用场景。例如,可以研究如何更好地选择基准元素以提高划分的平衡性;可以研究如何在保持稳定性的同时降低算法的时间复杂度和空间复杂度;还可以研究如何将快速排序算法与其他算法相结合以解决更复杂的问题。此外,随着大数据和人工智能技术的不断发展,快速排序算法在分布式计算、并行计算等领域的应用也值得进一步研究和探索。
![[HackMyVM]靶场Crossbow](https://img-blog.csdnimg.cn/direct/25827a67260046e886294dc1684a1748.png)