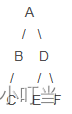思路分析：

1. 首先定义了一个Solution类，包含了私有成员变量fa[1001]和n，以及三个私有成员函数find()、togother()和findRedundantConnection()。

2. find()函数用于查找节点的根节点（即所在连通分量的代表节点），采用了递归方式实现路径压缩，以提高查找效率。

3. togother()函数用于将两个节点连接在一起，即将其中一个节点的父节点更新为另一个节点的父节点。

4. findRedundantConnection()函数用于寻找冗余连接的边，即能够形成环的边。首先初始化父节点数组fa[]，然后遍历所有的边，如果两个节点已经在同一个连通分量中，则说明当前边会形成环，记录下环中的两个节点。最后返回冗余连接的两个节点。

5. 在主函数中，首先创建Solution类的一个对象，然后调用findRedundantConnection()函数并传入边的二维数组，得到冗余连接的结果。

利用并查集（Union-Find）的思想，通过合并连通分量的方式，来判断图中是否存在环，从而找出冗余的边。

class Solution {
    int fa[1001]; // 用于记录节点的父节点
    int n; // 节点数量

    // 查找节点的根节点（父节点）
    int find(int x) {
        if (fa[x] == x)
            return x;
        else
            return find(fa[x]);
    }

    // 将两个节点连接在一起，即更新其中一个节点的父节点为另一个节点的父节点
    void togother(int x, int y) {
        fa[find(x)] = find(y);
    }

public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        n = edges.size();

        // 初始化父节点数组，每个节点的父节点初始设为自己
        for (int i = 0; i < n; i++) {
            fa[i] = i;
        }

        int u, v; // 记录冗余连接的两个节点
        // 遍历所有的边
        for (int i = 0; i < n; i++) {
            // 如果两个节点已经在同一个连通分量中，说明当前边会形成环
            if (find(edges[i][0]) == find(edges[i][1])) {
                u = edges[i][0]; // 记录环中的其中一个节点
                v = edges[i][1]; // 记录环中的另一个节点
            }
            // 否则将当前边的两个节点连接在一起
            togother(edges[i][0], edges[i][1]);
        }

        // 返回冗余连接的两个节点，这里返回的是数组edges中最后出现的冗余连接
        return {u, v};
    }
};