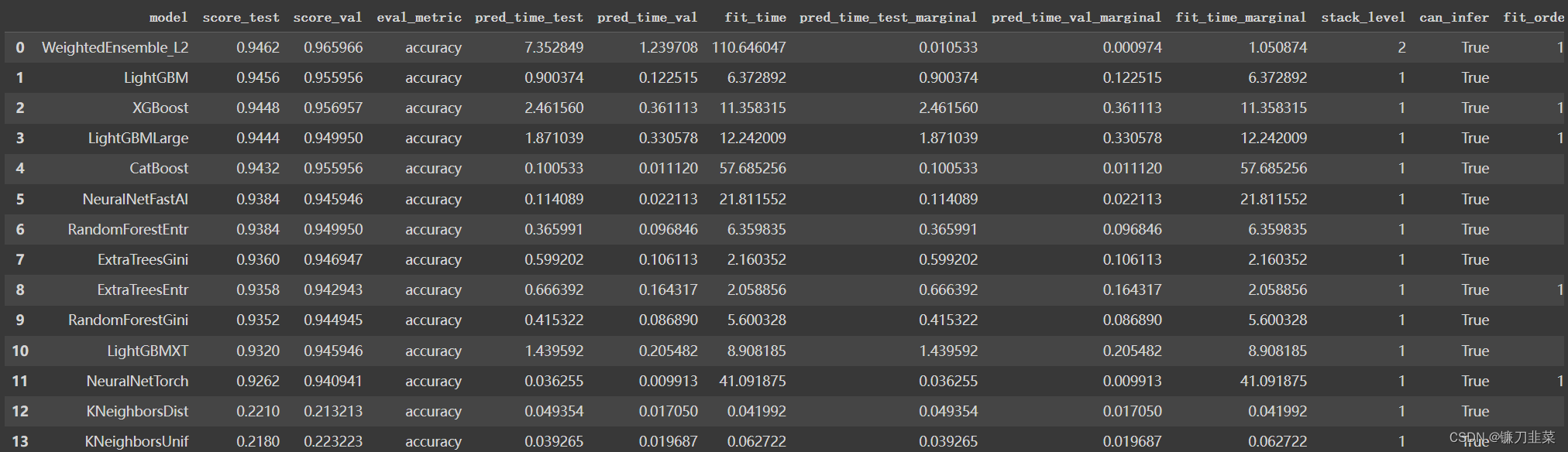
Finding both the minimum and maximum in an array of integers A[1..n] and assume for simplicity that n is a power of 2

  1. x←A[1]; y←A[1]

  2. for i←2 to n

  3.   if A[i] < x then x←A[i]

  4.   if A[i] > y then y←A[i]

  5. end for

  6. return (x, y)

        Clearly, the number of element comparisons performed by this method is 2n−2

1. 输入参数：该过程接受两个参数 low 和 high，表示数组 A 中待处理的范围。

2. 基本情况处理：首先检查待处理范围是否只有一个元素。如果是，直接比较这两个元素的大小，返回一个包含最小值和最大值的元组。如果不是，继续进行后续处理。

3. 递归分治：如果待处理范围不止一个元素，则计算中间位置 mid，并递归调用 minmax 过程来处理左右两个子范围 (low, mid) 和 (mid + 1, high)。

4. 合并结果：得到子范围的最小值和最大值后，分别用变量 (x1, y1) 和 (x2, y2) 来表示。然后，取这两个子范围的最小值 x 和最大值 y：

   • 最小值 x 是 x1 和 x2 中的较小者。
   • 最大值 y 是 y1 和 y2 中的较大者。

5. 返回结果：最后，以元组 (x, y) 的形式返回结果。

         Let C(n) denote the number of comparisons performed by the algorithm on an array of n elements, where n is a power of 2.  Note that the element comparisons are performed only in steps 2, 9, and 10. Also note that the number of comparisons performed by steps 7 and 8 as a result of the recursive calls is C(n/2). This gives rise to the following recurrence relation for the number of comparisons done by the algorithm:

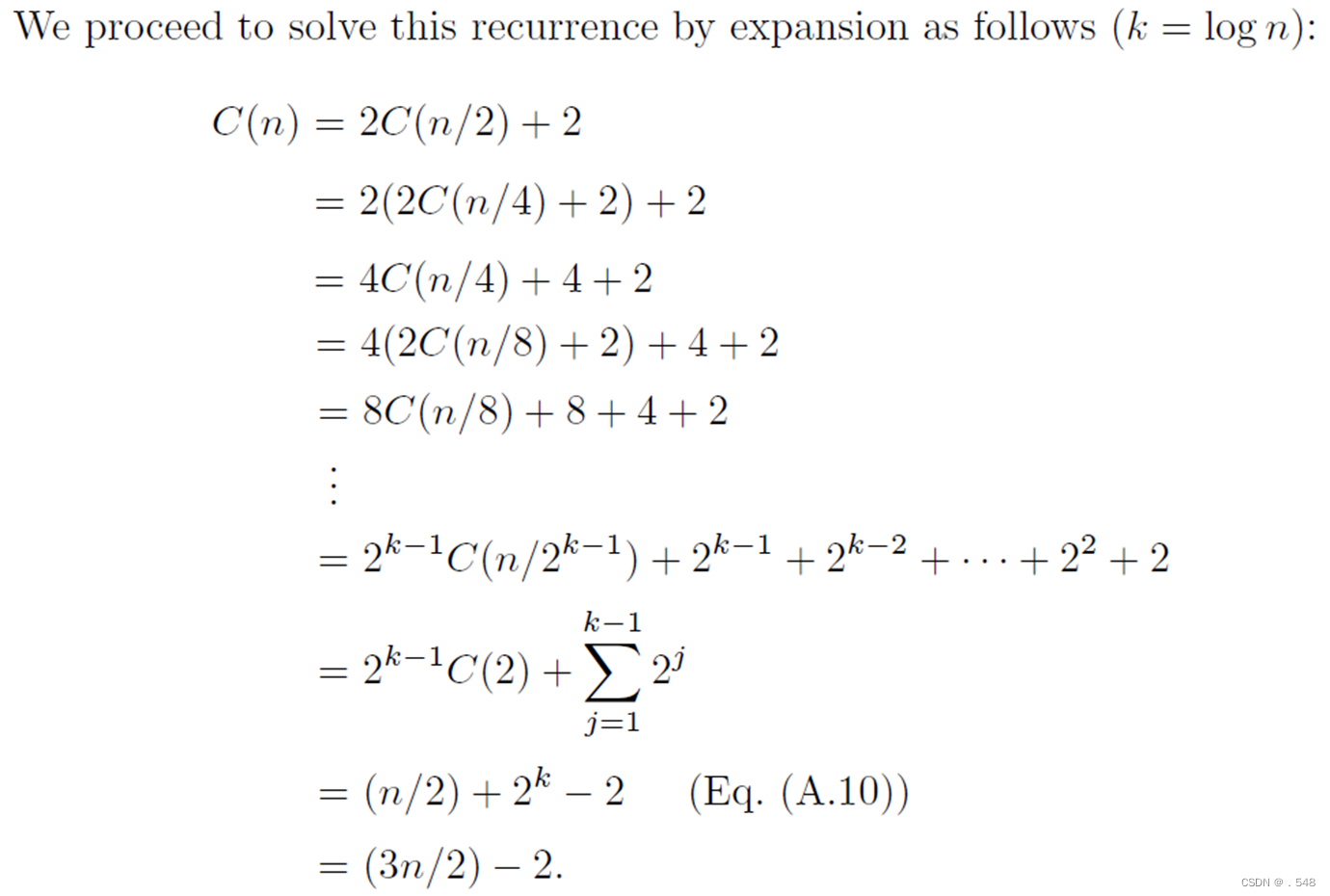
A = [3, 8, 6, 2, 11, 5, 9, 4]

现在我们想要找出数组 A 中索引范围为 0 到 7 的最小值和最大值。

1. 输入参数：调用 minmax(0, 7)，表示在数组 A 中索引范围为 0 到 7 的子数组中查找最小值和最大值。

2. 基本情况处理：由于索引范围不止一个元素，因此我们继续进行后续处理。

3. 递归分治：我们计算中间位置 mid = (low + high) // 2 = (0 + 7) // 2 = 3，然后分别递归地调用 minmax(0, 3) 和 minmax(4, 7)。

4. 左子范围处理：对于子范围 (0, 3)，继续递归调用 minmax(0, 1) 和 minmax(2, 3)。

   • 对于子范围 (0, 1)，由于只有一个元素，返回 (3, 3)。
   • 对于子范围 (2, 3)，由于只有一个元素，返回 (2, 6)。

5. 左子范围合并结果：左子范围的最小值是 3，最大值是 6。

6. 右子范围处理：对于子范围 (4, 7)，继续递归调用 minmax(4, 5) 和 minmax(6, 7)。

   • 对于子范围 (4, 5)，由于只有一个元素，返回 (5, 11)。
   • 对于子范围 (6, 7)，由于只有一个元素，返回 (9, 9)。

7. 右子范围合并结果：右子范围的最小值是 5，最大值是 11。

8. 合并结果：最后，合并左右子范围的结果。最小值为 min(3, 5) = 3，最大值为 max(6, 11) = 11。

9. 返回结果：返回最终的结果 (3, 11)，表示数组 A 中索引范围为 0 到 7 的最小值是 3，最大值是 11。