目录

0. 引言

1. priority_queue 介绍 

1.1 构造函数 

1.2 priority_queue 接口函数使用 

1.3 仿函数 

 1.4 题目练习

 2. priority_queue 模拟实现

2.1基本框架：

2.2 默认构造函数

2.3 基本函数

2.4 堆的向上以及向下调整

---

0. 引言

优先队列 (priority_queue) 是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)。优先队列和堆本质是一样的，以数组形式存储的完全二叉树。

1. priority_queue 介绍 

1.1 构造函数 

我们可以看到有两种构造方式，一个是构造一个空对象，另一个是通过迭代器的区间来构造，默认的构造出的是大堆。

priority_queue<int> pq1; //直接构造空对象

接下来我们分别以大堆和小堆的方式来构造对象：

	vector<int> v1 = {3,2,7,6,0,4,1,9,8,5};
	priority_queue<int, vector<int>, less<int>> pq1(v1.begin(), v1.end());
                                    //less-大堆
	while (!pq1.empty())
	{
		cout << pq1.top() << " ";
		pq1.pop();
	}
	cout << endl;

	priority_queue<int, vector<int>, greater<int>> pq2(v1.begin(), v1.end());
                                    //greater-小堆
	while (!pq2.empty())
	{
		cout << pq2.top() << " ";
		pq2.pop();
	}
	cout << endl;

	priority_queue<int> pq3(v1.begin(), v1.end());
                                    //默认大堆
	while (!pq3.empty())
	{
		cout << pq3.top() << " ";
		pq3.pop();
	}
	cout << endl;

因此我们得出： less - 大堆， greater - 小堆。 

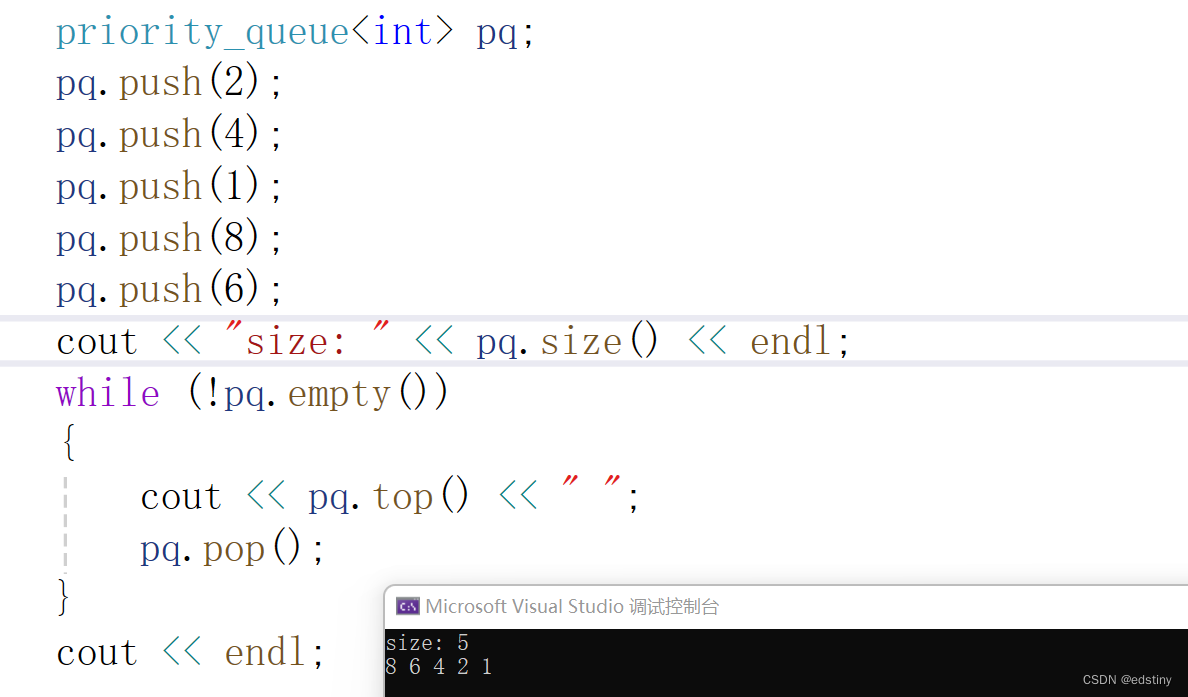
1.2 priority_queue 接口函数使用 

接口函数主要包括以下：

函数	说明
empty	检测优先级队列是否为空，是返回true，否则返回 false
top	返回优先级队列中最大(最小元素)，即堆顶元
push	在优先级队列中插入元素x
pop	删除优先级队列中最大(最小)元素，即堆顶元素

1.3 仿函数 

仿函数又名函数对象 function objects 仿函数的主要作用是借助类和运算符重载，做到同一格式兼容所有函数。由于模板将 less 用作大堆，而 greater 用做小堆，是在有点别扭，如果是我们自己实现仿函数的化，肯定会按照习惯来写，less 表示小堆，greater 表示大堆。例如：

template<class T>
struct less
{
	bool operator()(const T& x, const T& y)
	{
		return x < y;
	}
};

template<class T>
struct greater
{
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};

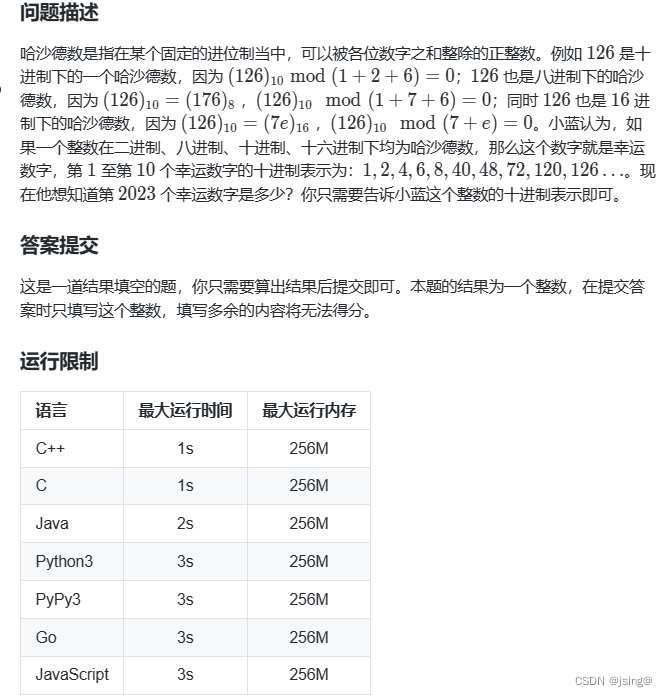
 1.4 题目练习

优先级队列适合来进行TOPK 以及 排序问题，因为其底层是和堆一模一样的。现在我们一起来看下面这道题：

这题如果不关心时间复杂度，直接利用 sort 排序将会很简单：

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
        sort(nums.begin(),nums.end());
        return nums[nums.size()-k];    
    }
};

 当我们使用优先级队列时，时间复杂度会更好：

//大堆
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
    priority_queue<int> pq1(nums.begin(), nums.end());
      for(int i = 0;i < k-1; i++)
      {
            pq1.pop();
      }
       return pq1.top(); 
    }
};

//小堆
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
    priority_queue<int,vector<int>, greater<int>> pq1(nums.begin(), nums.begin()+k);
    for(int i = k ;i < nums.size(); i++)
    {
        if(nums[i] > pq1.top())
        {
            pq1.pop();
            pq1.push(nums[i]);
        }
    }
    return pq1.top(); 
    }  
};

 2. priority_queue 模拟实现

 优先级队列的模拟实现，难点在于堆的 向上和向下调整。

2.1基本框架：

#pragma once

#include <vector>

namespace LHY
{
	//默认底层结构为 vector
	template<class T, class Container = std::vector<T>>
	class priority_queue
	{
	public:
		//构造函数及其他功能
	private:
		Container _con;	//其中的成员变量为底层容器对象
	};
}

2.2 默认构造函数

//默认构造函数
priority_queue()
	:_con()
{}

//迭代器区间构造
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)
	:_con()
{
	while (first != last)
	{
		push(*first);
		first++;
	}
}

2.3 基本函数

//判断是否为空
bool empty() const
{
	return _con.empty();
}

//优先级队列的大小（有效元素数）
size_t size() const
{
	return _con.size();
}

//堆顶元素（优先级最 高/低 的值）
const T& top() const
{
	return _con.front();
}

2.4 堆的向上以及向下调整

//向上调整
void adjust_up(size_t child)
{
	size_t parent = (child - 1) / 2;

	while (child != 0)
	{
		//父 > 子 此时为大堆，如果不符合，则调整
		if (_con[child] > _con[parent])
		{
			std::swap(_con[child], _con[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}
//向下调整
void adjust_down(size_t parent)
{
	size_t child = parent * 2 + 1;	//假设左孩子为 【大孩子 / 小孩子】

	while (child < size())
	{
		//判断右孩子是否比左孩子更符合条件，如果是，则切换为与右孩子进行比较
		if (child + 1 < size() && _con[child + 1] > _con[child])
			child++;

		//父 > 子 此时为大堆，如果不符合，则调整
		if (_con[child] > _con[parent])
		{
			std::swap(_con[child], _con[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;	//满足条件时，一样需要跳出，不再调整
	}
}

 

---