目录
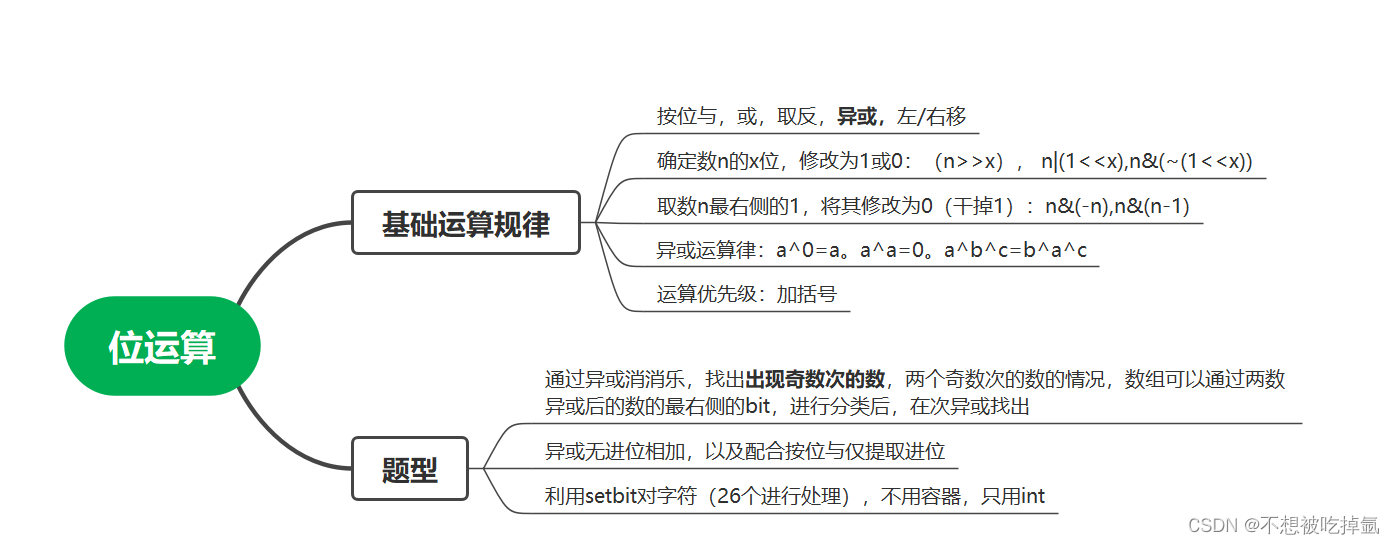
常见位运算:
1、基础位运算
2、对于一个数n。确定、修改这个数n二进制x位。
3、提取(确定)一个数n最右侧的1(bit)与干掉最右侧的1(bit)
4、异或运算律
5、位运算的优先级:加括号
6、练习
常见位运算:
1、基础位运算
按位与、或、取反、异或、算术右移、算术左移:& 、|、~、^、>>、<<。
与:有0是0,全1为1;
或:有1是1,全0为0;
取反:按位取反
异或:相同为0,不同为1,同时异或也是无进位相加。(重点)
算术右移:仅对于有符号数,对于无符号数为逻辑右移
算术左移:仅对于有符号数,对于无符号数为逻辑左移,逻辑左移与算术右移操作一样无区别。
注意:算术和逻辑左/右移指的是一种特定操作。
2、对于一个数n。确定、修改这个数n二进制x位。
注:x为数n的范围内任意位
确定某位: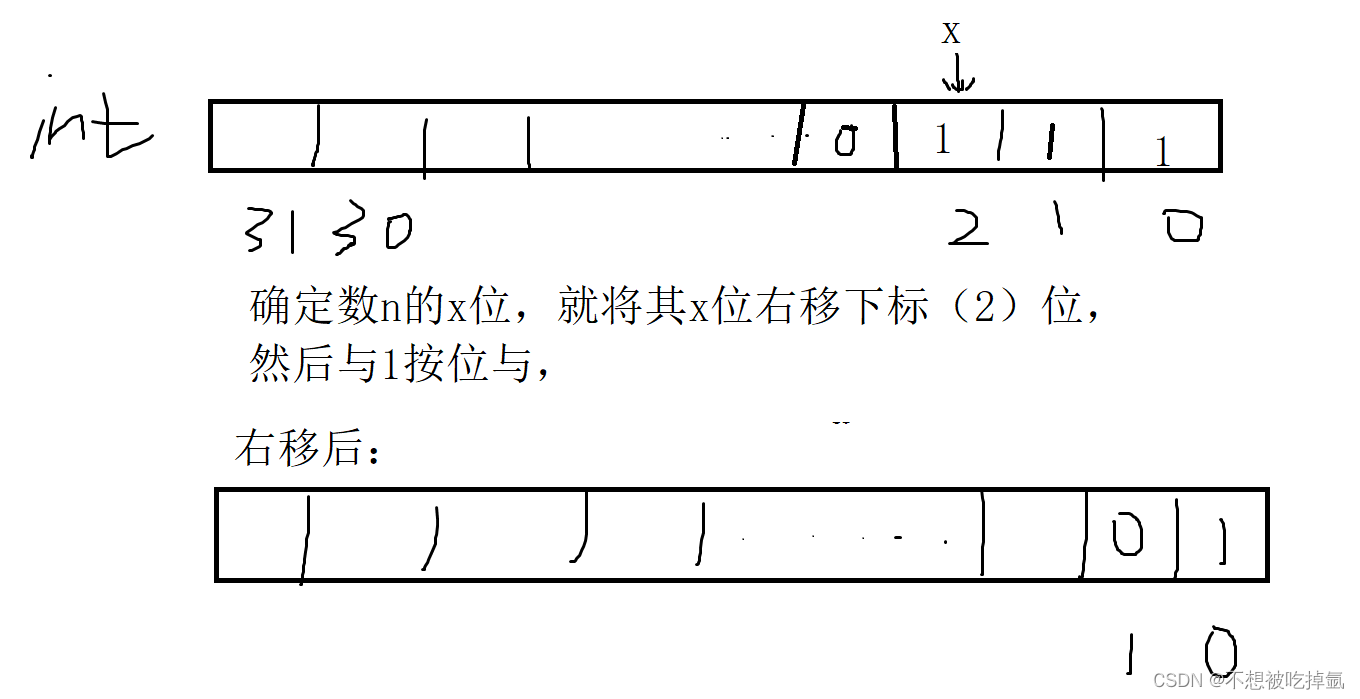
(int)1的 二进制为:000000……0001;按位与1后,除最低位外所有位变为0,判断最低位,为1,所有数n的x位为1,反之为0。
(n>>x)&1==1? 1:0;//数n的x位为1,返回1,为0返回0。修改某位为1:
将(int)1左移x位,变成如下:
然后与数n按位或 ,(bit)0与任意或为任意,1与任意或为1,所有将数n的x位置为1。
n=n|(1<<x);//修改数n的x位为1。
修改某位为0:
将(int)1左移x位,在按位取反,变成如下,除了x位外都为1.
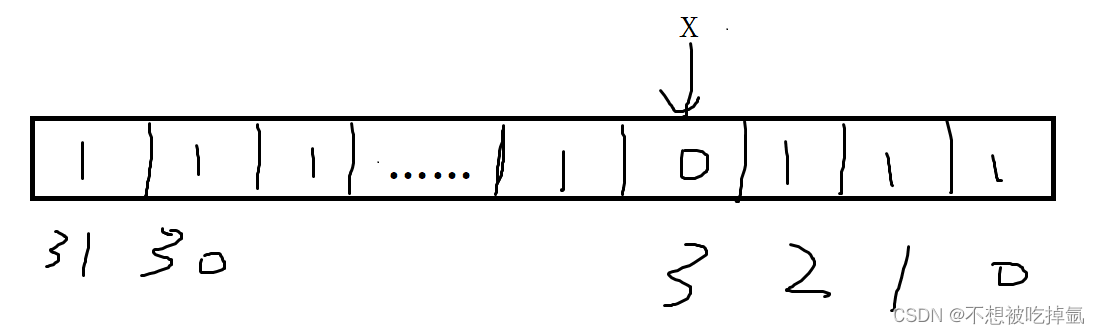
然后与数n按位与,(bit)1与任意与为任意,0与任意与为0,所以将数n的x位置变为0。
n=n&(~(1<<x));//修改n的x位为0.小结:setbit(位图) 利用的就是这种思想。setbit就是一种特殊的hash表,用一个bit位来存储状态信息。
3、提取(确定)一个数n最右侧的1(bit)与干掉最右侧的1(bit)
原理:-n为:将最右侧的1的左边的数全部取反,然后与数n相与。
bit=n&(-n);原理:n-1为将最右侧的1的右边的数全部取反,然后与数n相与
n=n&(n-1);4、异或运算律
a^0=a;//
a^a=0;//消消乐
a^b^c=a^c^b;//交换律例题:136. 只出现一次的数字 - 力扣(LeetCode)
思路:同数异或相消
260. 只出现一次的数字 III - 力扣(LeetCode)
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int Xor=0;
for(int num:nums) { //取出两个一次数相互异或所得数
Xor^=num;
}
int sub =(Xor==INT_MIN ? Xor:Xor&(-Xor));//-128对于128超出范围
int type1 =0,tyep2=0;
for(int num:nums){
if(sub&num) type1^=num;
else tyep2^=num;
}
return {type1,tyep2};
}
};5、位运算的优先级:加括号
6、练习
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
class Solution {
public:
bool isUnique(string astr) {
if(astr.size()>26) return false;
int bitset=0;//位图
for(char ch:astr){
int i=ch-'a'; //字符映射到bitset的第i位
if((bitset>>i)&1) return false; //判断bitset的第i位的值是否为1
//bitset存入状态
bitset=bitset|(1<<i);
}
return true;
}
};268. 丢失的数字 - 力扣(LeetCode)
思路:同数异或相消
371. 两整数之和 - 力扣(LeetCode)
class Solution {
public:
int getSum(int a, int b) {//利用无进位相加
while(b!=0){
int x=a^b;//无进位相加
int carry=(a&b)<<1;//进的位的值
a=x;b=carry;//循环直到b=0,表示没有进位
}
return a;
}
};137. 只出现一次的数字 II - 力扣(LeetCode)
class Solution {
public:
int singleNumber(vector<int>& nums) {//通过位运算,得出每一位的0还是1.
int ret=0;
for(int i=0;i<32;i++){
int sum=0;
for(int val:nums){
if(((val>>i)&1)==1) sum+=1;//3n+1或3n+0
}
if(sum%3==1){
ret|=(1<<i);
}
}
return ret;
}
};可以推广到:只出现一次的数字(如果是两个?不可以,无法获得两个数的异或来分类),其他的数都出现n次。
面试题 17.19. 消失的两个数字 - 力扣(LeetCode)
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int n=nums.size();
int N=n+2;//1~N个数字,构建只出现一次的两个数
//异或相消,
int Xor=0;
for(int num:nums){
Xor^=num;
}
for(int i=1;i<N+1;i++){
Xor^=i;
}
//此时Xor为消失的两数字相互异或,通过最低位区分两个不同的数
int sub=Xor==INT_MIN?Xor:Xor&(-Xor);//根据缺失两数的最低位不同
int type1=0,type2=0;
for(int num:nums){
if((num&sub)==0) type1^=num;
else type2^=num;
}
for(int i=1;i<N+1;i++){
if((i&sub)==0) type1^=i;
else type2^=i;
}
return {type1,type2};
}
};算法原理: 通过添加构建1~N,将问题降级为仅有两个仅出现一次的数字。