文章目录
- Git快速入门
- 1.Git概述
- 2.SCM概述
- 3.Git安装
- 3.1 软件下载
- 3.2 软件安装
- 3.3 软件测试
Git快速入门
1.Git概述

- Git是一个免费的,开源的分布式版本控制系统,可以快速高效地处理从小型到大型的各种项目,Git易于学习,占用空间小,性能快得惊人。
2.SCM概述
SCM(Software Configuration Management,软件配置管理)是一种标识、组织和控制修改的技术。它应用于整个软件生存周期。
作为评价一个大中型软件开发过程是否正确,合理,有效的重要手段,CMM(Capability Maturity Model )能力成熟度模型提供了不同等级的标准流程,对软件开发过程(流程)进行了约束和建议, 而作为CMM 2级的一个关键域(Key Practice Area,KPA),SCM软件在整个软件的开发活动中占有很重要的位置。
Git软件比Subversion、CVS、Perforce和ClearCase等SCM(Software Configuration Management软件配置管理)工具具有性价比更高的本地分支、方便的暂存区域和多个工作流等功能。
3.Git安装
3.1 软件下载
软件官网地址为:https://git-scm.com/
软件下载地址为:
https://github.com/git-for-windows/git/releases/download/v2.40.0.windows.1/Git-2.40.0-64-bit.exe

最早Git是在Linux上开发的,很长一段时间内,Git也只能在Linux和Unix系统上跑。不过,慢慢地有人把它移植到了Windows上。现在,Git可以在Linux、Unix、Mac和Windows这几大平台上正常运行了。由于开发机大多数情况都是windows,所以本教程选择相对简单的Windows系统软件版本进行下载,此处我们下载Windows系统的2.40.0版本软件

3.2 软件安装
Git软件安装的步骤虽然比较多,但是整个安装过程还是比较简单的,双击exe执行文件,按照引导界面的提示安装即可
点击Next下一步,选择安装目录,默认安装在c盘中
点击Next下一步,选择组件,此处默认即可
点击Next下一步,配置启动菜单,此处默认即可
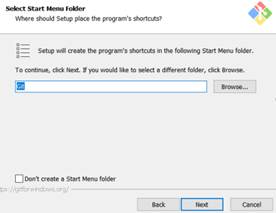
点击Next下一步,配置编辑器工具,这里选择自己习惯的编辑工具即可。

后续就不需要进行什么特殊配置了,所以连续默认选择Next下一步即可。
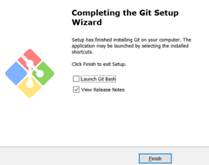
3.3 软件测试
在Windows桌面空白处,点击鼠标右键,弹出右键菜单
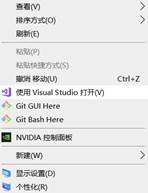
Git软件安装后,会在右键菜单中增加两个菜单
-
Git GUI Here
-
Git Bash Here
此处仅仅是为了验证Git软件安装的效果,所以选择Git Bash Here菜单, 选择后,Windows系统弹出Git软件的命令行黑窗口,
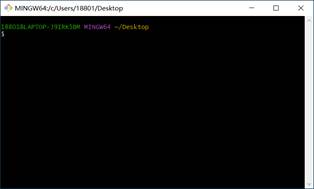
窗口弹出后,可以输入Git软件的操作指令。此时我们使用键盘输入操作指令:git -v或 git --version,查看当前Git软件的安装版本。
git -v
git -version
输入指令回车后,如果黑窗口中打印出咱们安装的软件版本2.40.0,Git软件安装成功了。