- BSD Alexey Pozdnyakov (University of Connecticut) YUTUBE视频, B站搬运地址
- 新生代女数学家Nina Zubrilina得到椭圆曲线椋鸟群飞模式精确公式与证明
Arithmetic Geometry算术几何
希尔伯特第十问题
-
希尔伯特第十问题(Hilbert’s Tenth Problem)是由德国数学家大卫·希尔伯特在1900年提出的一系列23个数学问题中的第十个问题。这个问题涉及到对于多项式方程是否存在一种通用的算法,用于判断方程是否有整数解。具体来说,希尔伯特问的是:
是否存在一个算法,能够确定一个给定的整系数多项式方程是否有整数解。 -
这个问题直到1970年才在苏联数学家尤里·马脱维奇·马特亚塔斯耶维奇·达尼洛维奇 (Yuri Matiyasevich) 的工作下得到回答。他证明了类似于戴尔宾斯(Julia Robinson)、马丁-戴维斯(Martin Davis)和普特南(Hilary Putnam)的一般形式的数学逻辑理论是适用于证明
这样的算法不存在的。 -
但是简单情况是有办法的。

-
我们只需要考虑一些更简单的问题和一种方法来做到这一点是限制多项式,我们看到限制它们的明显方法是查看变量较少且次数较低的多项式。
-
因此如果我们一直到单变量多项式,这个问题实际上就变成了有理根定理。允许我们确定该多项式是否有有理根
2-Variable Quadratics
- 如果我们有一个带有整数系数的二阶二变量多项式,

- 有两种情况, 要么没有有理解,要么有无限多个, 我们使用仓促的明可夫斯基定理来确定这一点,然后我们实际上可以明确地找到第二种情况下的所有解决方案呃
- 您只需找到一个有理解调用那个 p 然后你采取,通过 p 的所有有理斜率线并计算这些线与圆锥曲线的第二个交点,这实际上会给你所有有理点,这实际上会给你所有有理点
- 当然, 收集它们的线将具有合理的斜率,因为 x 和 a 会有合理的变化。
- y 的有理变化 um 反过来有点复杂,但本质上如果你有一条线穿过有理点以计算第二个交点。你把这条线插入二次曲线, 或者你把它代入, 嗯,这给你的是一个二阶一变量多项式,它具有所有有理系数, 并且你知道的根之一是有理数,因为它去有理点, 所以当然二阶也必须是理性的,嗯, 是的, 这基本上就是所有两个变量的情况
- 有点尴尬, 这是我们可以采取的最高情况。一旦你尝试处理更复杂的情况,哈西·明可夫斯基定理就会失败。
Mordell-Weil Theorem Over Q
椭圆曲线
- 所以如果你采用三次方程 3 x 立方加 4 y 立方加 5,就会有一个非常著名的反例z 那么这只有平凡的有理数解。
- 我们无法真正完全解决这些更困难的方程,所以这就是椭圆曲线出现的地方
- 椭圆曲线是属一的平滑射影代数曲线,平滑意味着没有尖点或扭结,或者导数永远不会同时消失射影意味着我们将在射影平面上工作
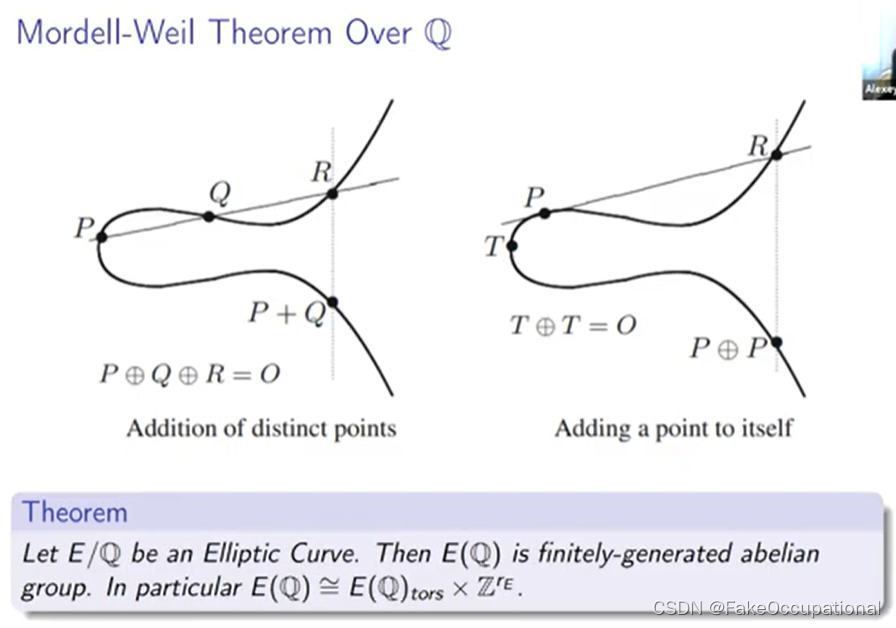
- 所以这个抽象定义与我们一直在研究的方程有一个定理,它说域 k 上的每个椭圆曲线 e 都同构于由以下方程给出的曲线, 正如您所看到的, 它是一个二变量三阶方程关于这个同构的另一件事是它总是可以将指定的点 o 发送为无穷远点
是的, 也许更令人惊讶的是这个定理的逆,所以每条光滑的三次曲线都同构于椭圆曲线- 系数的多项式条件, 因此椭圆曲线构成了所有可能的三次曲线的扎斯基开子集,当然这意味着它们在所有三次曲线的集合中是密集的。

- 所以这个定理基本上告诉我们如何在给定一些已知的有理点的情况下生成新的有理点,如果你有两个有理点 p 和 q 你可以画一个穿过这些点的线然后该线将在呃第三个点处与立方体相交,事实证明, 这一点总是有理数。
Simple Open Problems

Understanding Rank - BSD Conjecture
- 所以如果你让 e 超过 fp 成为一条椭圆曲线有限域,你可以定义这个特定的量 ap , ap 是 p 加一减去 fp 上该曲线上的点数
- 所以当你查看椭圆曲线 mod p 和 um 时,你有多少个解, 这个量本质上是一个错误对解数量的某种估计,独立于等级, 你可以计算出你期望有多少个解,

Strong form BSD Conjecture The L-function of an elliptic curve is defined to be
椭圆曲线的L函数
- 这是这些非常好的方程之一,它将一个非常分析的对象与一个非常代数的对象联系起来

ML探索

Logistic Regression

Logistic Regression Results
-
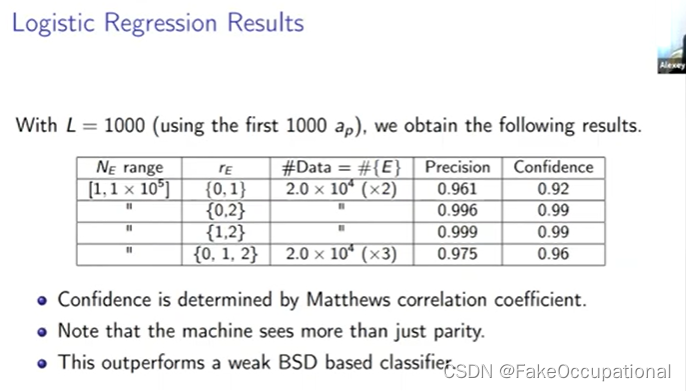
逻辑回归所做的事情与简单地近似不同,逻辑回归具有区分排名第一和排名第二的最佳性能,因此使用 bsd 公式排序,排名越远, 差异就越大。
-
但逻辑回归实际上表现最好区分排名一和排名二,逻辑回归是一种相当可解释的机器学习方法,只需查看该权重向量即可了解模型的 ap 依赖性。
-
特别是我们可以绘制权重向量的分量,并尝试了解它如何对不同 ap 进行加权,当我们这样做时, 我们会得到排名 0 与排名 1 的图模型。
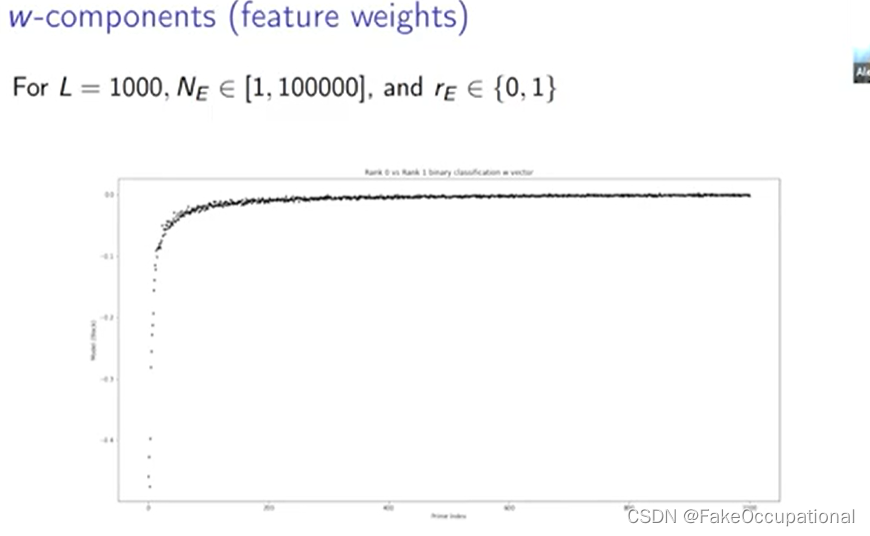
- 这里的所有或大部分权重都是负数,所以这意味着我们对 ap 进行负权重,这种情况是由 bsd 猜想解释的,
Principle Component Analysis (PCA)
- 我们还想尝试一种无监督学习方法,我们只需将其交给 ap 并让它对数据进行某种分析,我们所做的就是主成分分析 (PCA) 或主成分分析 (principal)。

PCA Result
- 这些是对排名 0、1 和 2 的每个排名的 12 000 条曲线进行采样的结果,似乎第一个主成分实际上是在排名上的,所以这告诉我们, ap 数据集中最大的方差实际上是由排名决定的
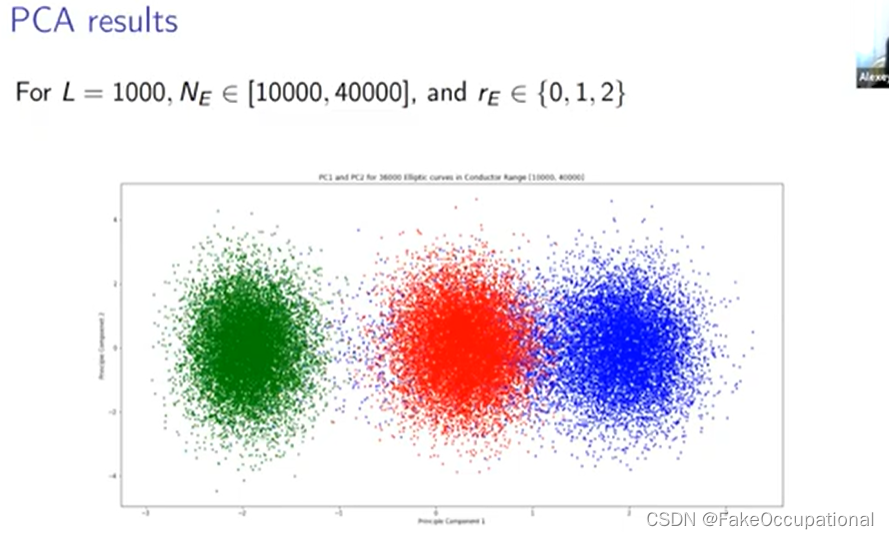
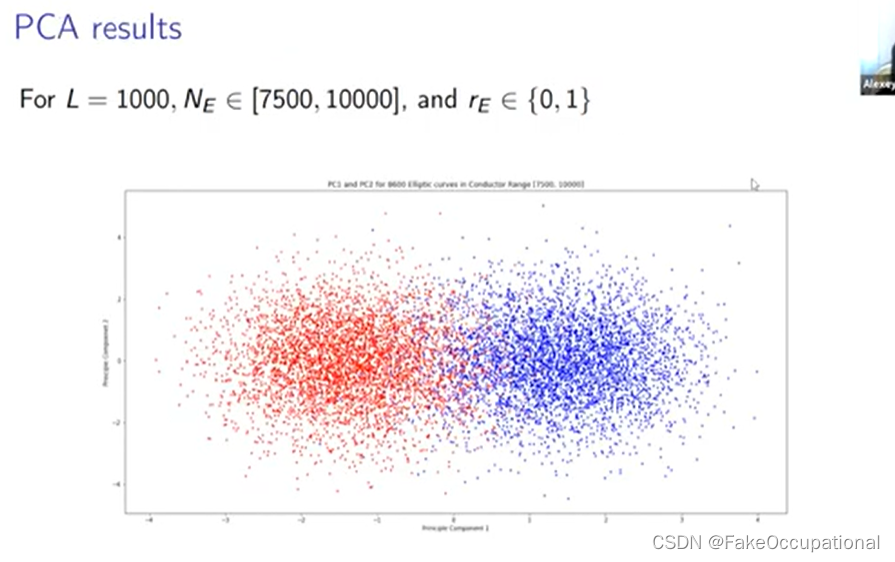
- 最后的 PCA 结果有点没有最好的分离,特别是在排名零和排名一之间
- 嗯, 我们感兴趣的一件事是尝试在两者之间获得更好的分离,因此我们能够通过首先删除所有排名二的点来做到这一点,
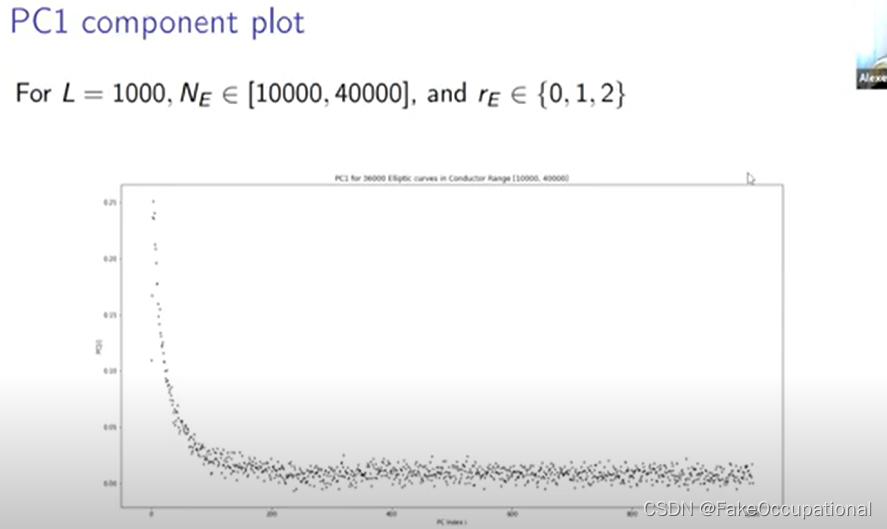
PC1 component plot
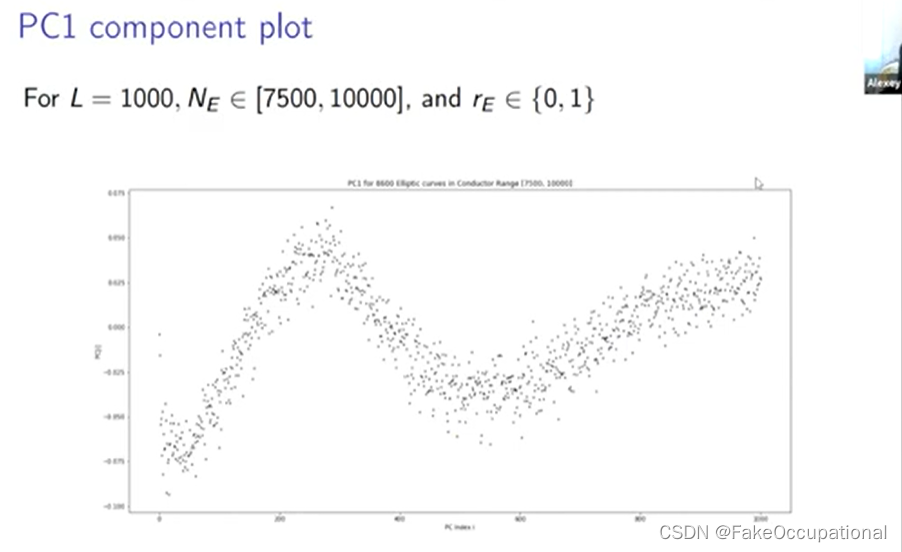
- 它不再是正值或负值,它在两者之间来回振荡,然后它从负值开始变得正也不再是前一百个 ap 中的大部分权重,正如您所看到的, 权重有点遵循这种平滑的振荡
- 这个主成分图的作用是告诉我们当我们将这些 ap 投影到低维子空间时我们采用什么 ap 的线性组合,在这个高维空间中, 平均等级零平均等级一曲线是什么样子
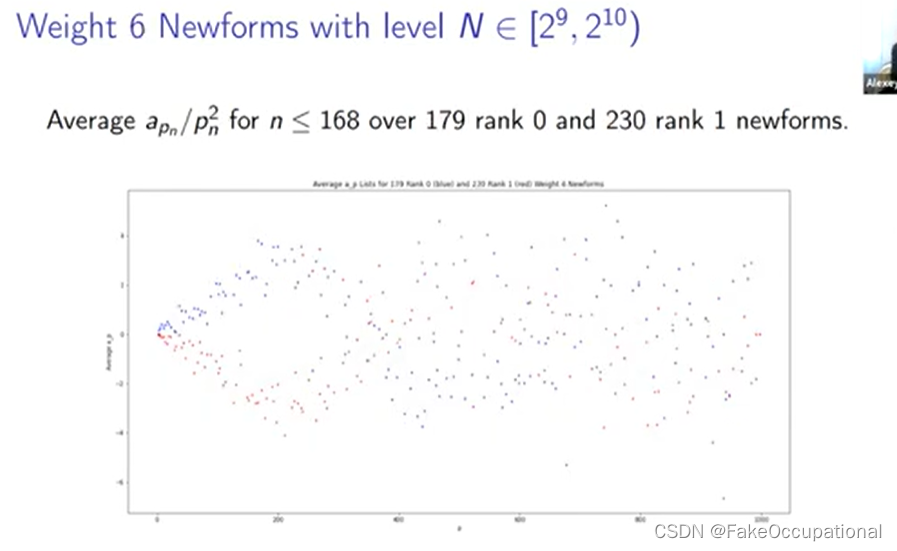
- 那么我们如何才能看看这条平均曲线,我们需要定义我们要平均的椭圆曲线集,所以我们在这里使用 n1 到 m2 的 er 来实现这一点,它只是秩等于 r 的所有椭圆曲线的集合
- 然后我们在这里定义这个函数,因此 n 的 fr 只是这整组椭圆曲线上的第 n 个 ap 的平均值,

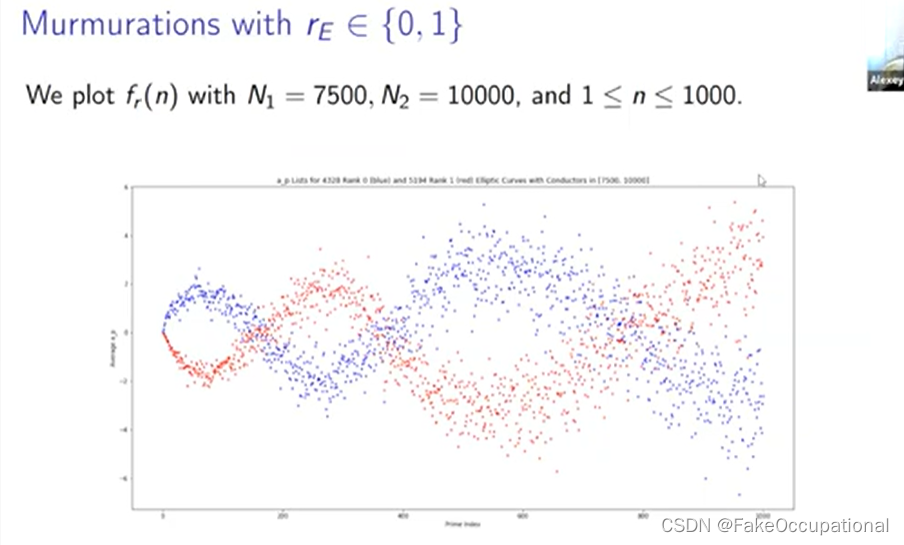
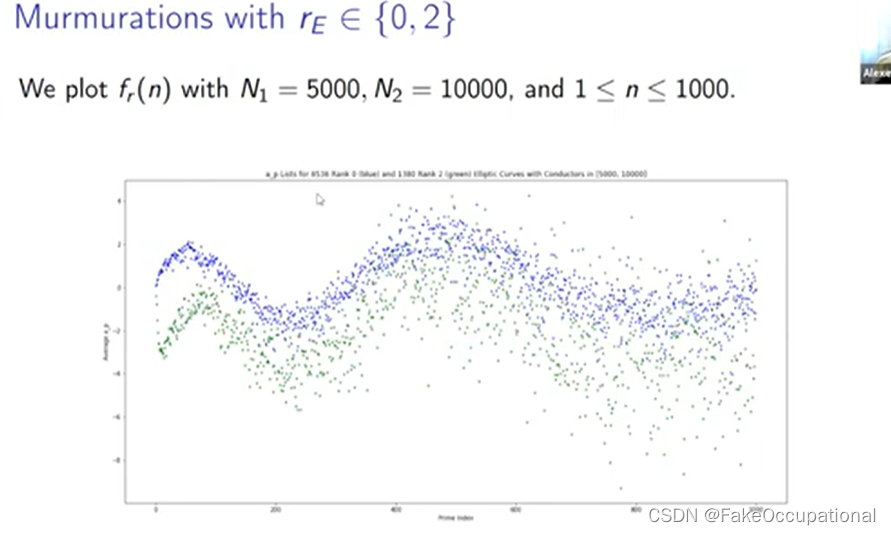
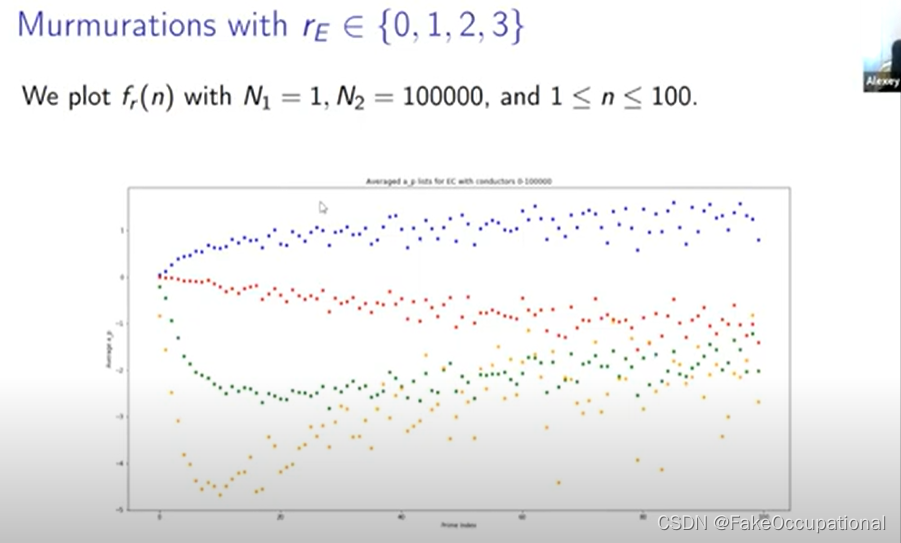
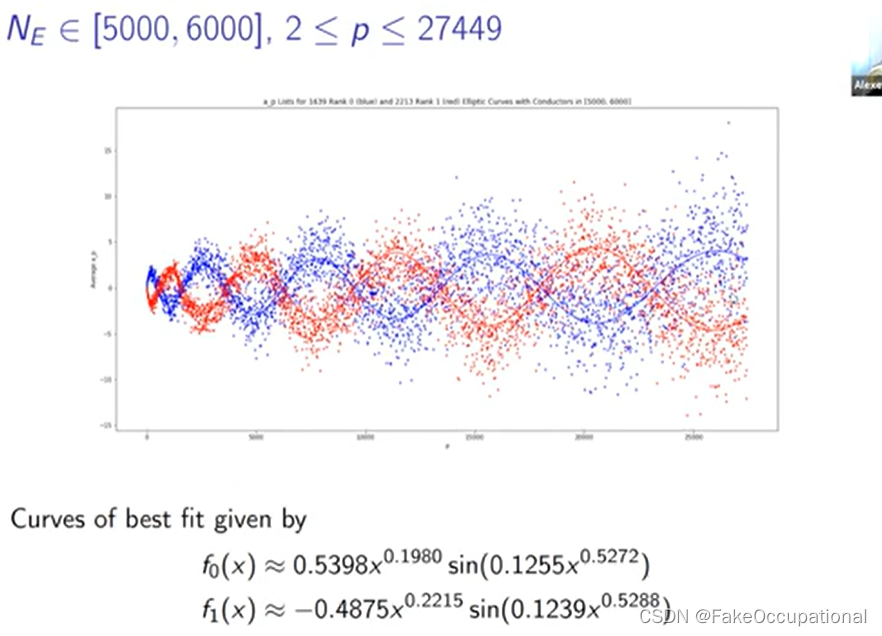
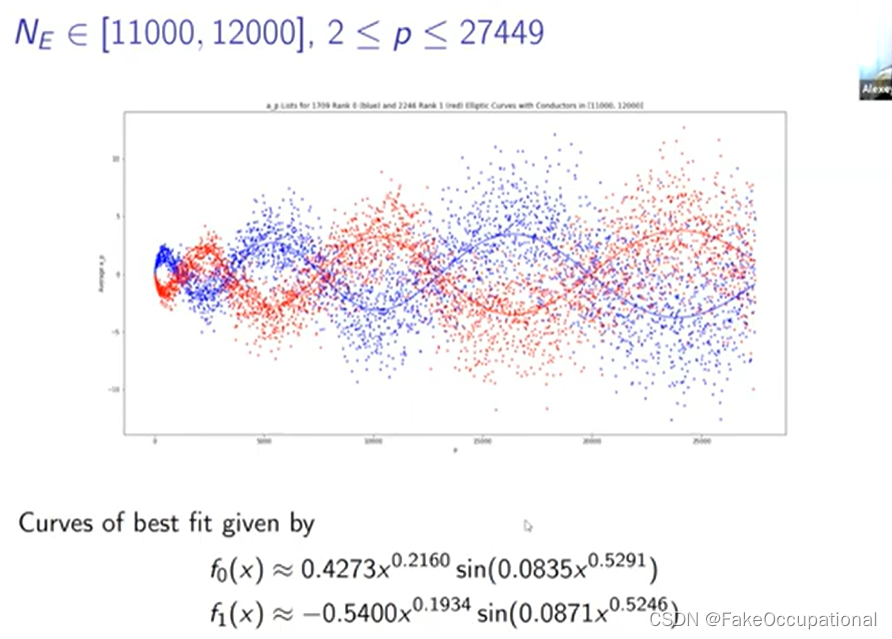
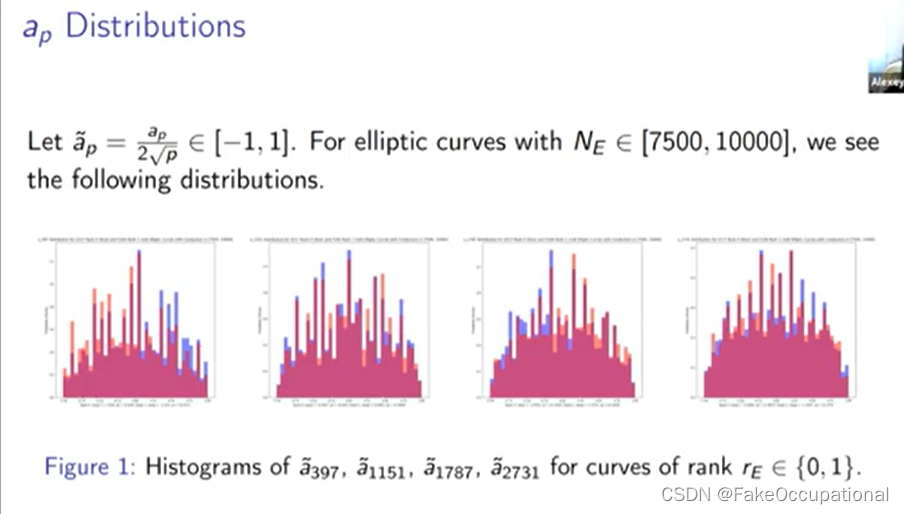
-
我们将排名零的分布绘制为蓝色,将排名一的分布绘制为红色,大多数分布是这个紫色重叠区域
-
我想简要谈谈我们一直在研究的这项工作的非常自然的延伸之一,所以嗯安德鲁·怀尔斯(andrew wiles)当他批准马的最后一个定理时,他的一个非常重要的关键步骤是他证明了某个椭圆曲线是模的,这意味着 l 函数将椭圆曲线与 a 的 l 函数关联起来或等于 a 的 l 函数某种模块化形式。从那时起, 这个结果得到了某种程度的扩展,特别是在 2001 年证明了有理数上的所有椭圆曲线都是模的,

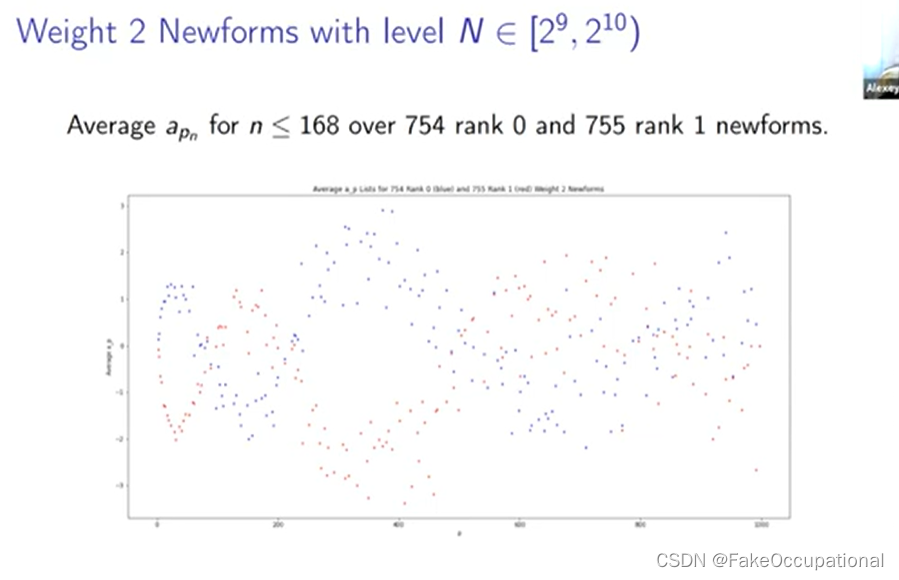
New Questions