前言

大家好，我是jiantaoyab，本篇文章给大家介绍数据出错和有什么方法能减少出错。

单比特翻转

由于硬件故障或其他原因，内存或其他存储设备中的单个比特位发生随机变化的现象。

例如，原本存储为1的位可能变为0，或者原本存储为0的位可能变为1。这种错误可能导致程序执行错误或数据损坏。

奇偶校验和校验位

其实，内存里面的单比特翻转或者错误，并不是一个特别罕见的现象。无论是因为内存的制造质量造成的漏电，还是外部的射线，都有一定的概率，会造成单比特错误。而内存层面的数据出错，软件工程师并不知道，而且这个出错很有可能是随机的。

可以用奇偶检验来发现这些错误，奇偶校验的思路很简单。把内存里面的 N 位比特当成是一组。

常见的，比如 8 位就是一个字节。然后，用额外的一位去记录，这 8 个比特里面有奇数个 1 还是偶数个 1。如果是奇数个 1，那额外的一位就记录为 1；如果是偶数个 1，那额外的一位就记录成 0。那额外的一位，我们就称之为校验码位。

如果在这个字节里面，我们不幸发生了单比特翻转，那么数据位计算得到的校验码，就和实际校验位里面的数据不一样。我们的内存就知道出错了。

除此之外，校验位有一个很大的优点，就是计算非常快，往往只需要遍历一遍需要校验的数据，通过一个 O(N) 的时间复杂度的算法，就能把校验结果计算出来。

不过，使用奇偶校验，还是有两个比较大的缺陷。

第一个缺陷，就是奇偶校验只能解决遇到单个位的错误，或者说奇数个位的错误。如果出现 2 个位进行了翻转，那么这个字节的校验位计算结果其实没有变，我们的校验位自然也就不能发现这个错误。

第二个缺陷，是它只能发现错误，但是不能纠正错误。所以，即使在内存里面发现数据错误了，我们也只能中止程序，而不能让程序继续正常地运行下去。

ECC内存

ECC 内存的全称是 Error-Correcting Code memory，中文名字叫作纠错内存。顾名思义，就是在内存里面出现错误的时候，能够自己纠正过来。

我们不仅能捕捉到错误，还要能够纠正发生的错误。这个策略，我们通常叫作纠错码（Error Correcting Code）又叫作纠删码（Erasure Code），不仅能够纠正错误，还能够在错误不能纠正的时候，直接把数据删除。

无论是我们的 ECC 内存，还是网络传输，乃至硬盘的 RAID，其实都利用了纠错码和纠删码的相关技术。

最知名的纠错码就是海明码。最基础的海明码叫7-4 海明码。这里的“7”指的是实际有效的数据，一共是 7 位（Bit）。而这里的“4”，指的是我们额外存储了 4 位数据，用来纠错。

纠错码的纠错能力是有限的。不是说不管错了多少位，我们都能给纠正过来。在 7-4 海明码里面，我们只能纠正某 1 位的错误。

4 位的校验码，一共可以表示 2^4 = 16 个不同的数。根据数据位计算出来的校验值，一定是确定的。所以，如果数据位出错了，计算出来的校验码，一定和确定的那个校验码不同。那可能的值，就是在 2^4 - 1 = 15 那剩下的 15 个可能的校验值当中。

15 个可能的校验值，其实可以对应 15 个可能出错的位。这个时候你可能就会问了，既然我们的数据位只有 7 位，那为什么我们要用 4 位的校验码呢？用 3 位不就够了吗？2^3 - 1 = 7，正好能够对上 7 个不同的数据位啊！

别忘了单比特翻转的错误，不仅可能出现在数据位，也有可能出现在校验位。校验位本身也是可能出错的。所以，7 位数据位和 3 位校验位，如果只有单比特出错，可能出错的位数就是 10 位，2^3 - 1 = 7 种情况是不能帮我们找到具体是哪一位出错的。

事实上，如果我们的数据位有 K 位，校验位有 N 位。那么我们需要满足下面这个不等式，才能确保我们能够对单比特翻转的数据纠错。这个不等式就是：
$$K+N+1<=2^N$$
在有 7 位数据位，也就是 K=7 的情况下，N 的最小值就是 4。4 位校验位，其实最多可以支持到 11 位数据位。

海明码的纠错原理

例如来算一个4-3 海明码（也就是 4 位数据位，3 位校验位）。

我们把 4 位数据位，分别记作 d1、d2、d3、d4。这里的 d，取的是数据位 data bits 的首字母。我们把 3 位校验位，分别记作 p1、p2、p3。这里的 p，取的是校验位 parity bits 的首字母。

从 4 位的数据位里面，我们拿走 1 位，然后计算出一个对应的校验位。这个校验位的计算用之前讲过的奇偶校验就可以了。

比如，我们用 d1、d2、d4 来计算出一个校验位 p1；用 d1、d3、d4 计算出一个校验位 p2；用 d2、d3、d4 计算出一个校验位 p3。就像下面这个对应的表格一样：

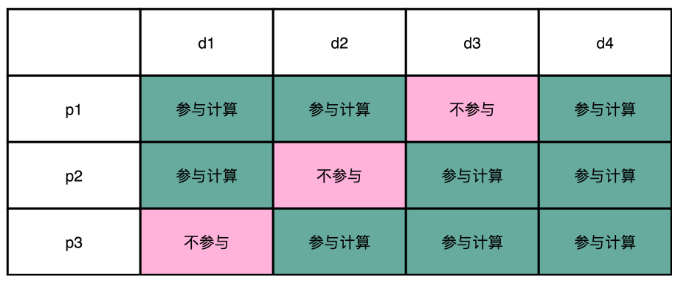
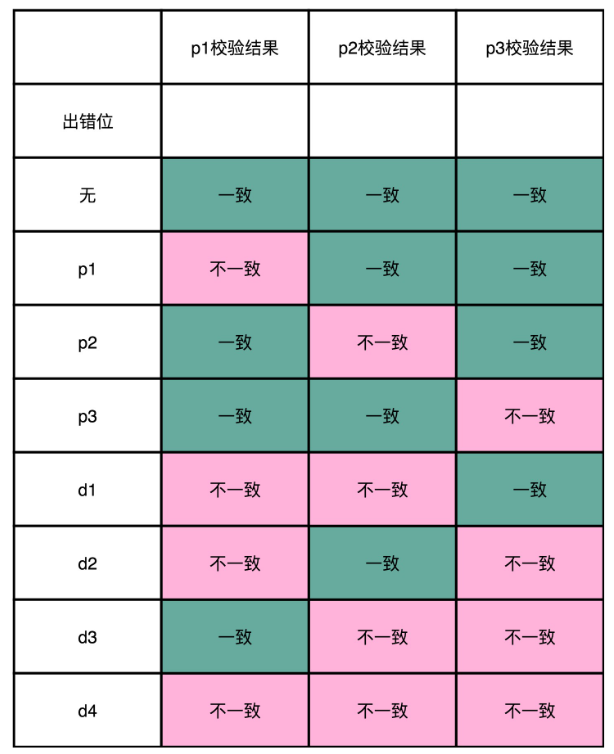
这个时候如果 d1 这一位的数据出错了，会发生什么情况？

我们会发现，p1 和 p2 和校验的计算结果不一样。d2 出错了，是因为 p1 和 p3 的校验的计算结果不一样；d3 出错了，则是因为 p2 和 p3；如果 d4 出错了，则是 p1、p2、p3 都不一样。你会发现，当数据码出错的时候，至少会有 2 位校验码的计算是不一致的。

那我们倒过来，如果是 p1 的校验码出错了，会发生什么情况呢？这个时候，只有 p1 的校验结果出错。p2 和 p3 的出错的结果也是一样的，只有一个校验码的计算是不一致的。

所以校验码不一致，一共有 2^3-1=7 种情况，正好对应了 7 个不同的位数的错误。

生成海明威码

比如说，我们这里的 7-4 海明码，就是一共 11 位。

然后，我们给这 11 位数据从左到右进行编号，并且也把它们的二进制表示写出来。

接着，我们先把这 11 个数据中的二进制的整数次幂找出来。在这个 7-4 海明码里面，就是 1、2、4、8。这些数，就是我们的校验码位，我们把他们记录做 p1～p4。如果从二进制的角度看，它们是这 11 个数当中，唯四的，在 4 个比特里面只有一个比特是 1 的数值。

那么剩下的 7 个数，就是我们 d1-d7 的数据码位了。

然后，对于我们的校验码位，我们还是用奇偶校验码。但是每一个校验码位，不是用所有的 7 位数据来计算校验码。而是 p1 用 3、5、7、9、11 来计算。也就是，在二进制表示下，从右往左数的第一位比特是 1 的情况下，用 p1 作为校验码。

剩下的 p2，我们用 3、6、10、11 来计算校验码，也就是在二进制表示下，从右往左数的第二位比特是 1 的情况下，用 p2。那么，p3 自然是从右往左数，第三位比特是 1 的情况下的数字校验码。而 p4 则是第四位比特是 1 的情况下的校验码。

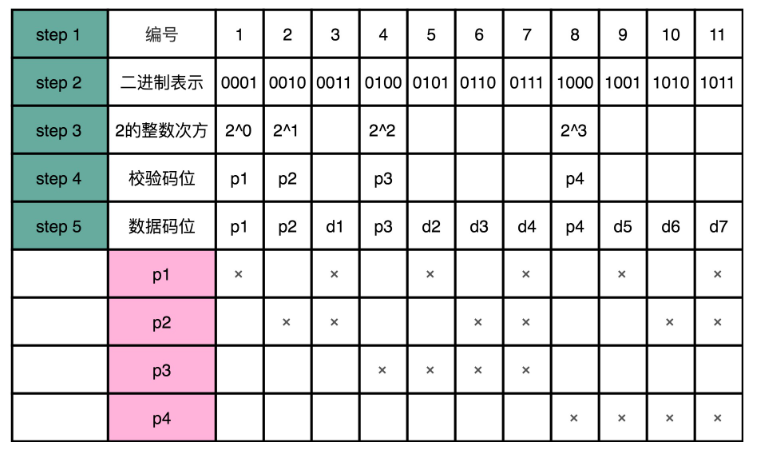
这个时候，任何一个数据码出错了，就至少会有对应的两个或者三个校验码对不上，这样我们就能反过来找到是哪一个数据码出错了。如果校验码出错了，那么只有校验码这一位对不上，我们就知道是这个校验码出错了。

海明距离

其实，我们还可以换一个角度来理解海明码的作用。

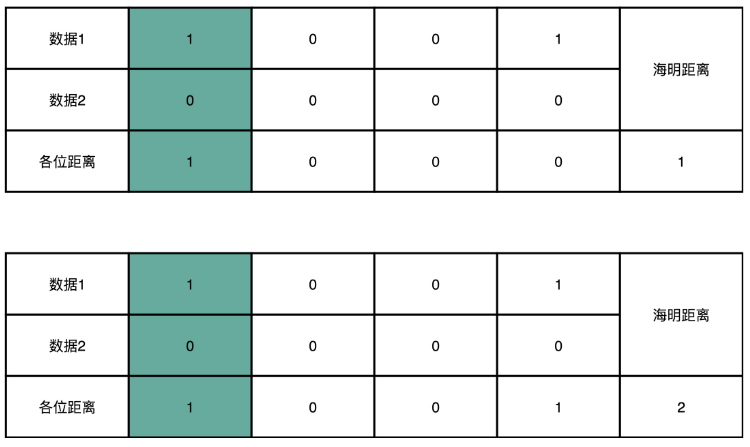
对于两个二进制表示的数据，他们之间有差异的位数，我们称之为海明距离。比如 1001 和 0001 的海明距离是 1，因为他们只有最左侧的第一位是不同的。而 1001 和 0000 的海明距离是 2，因为他们最左侧和最右侧有两位是不同的。

所谓的进行一位纠错，也就是所有和我们要传输的数据的海明距离为 1 的数，都能被纠正回来。而任何两个实际我们想要传输的数据，海明距离都至少要是 3。你可能会问了，为什么不能是 2 呢？因为如果是 2 的话，那么就会有一个出错的数，到两个正确的数据的海明距离都是 1。当我们看到这个出错的数的时候，我们就不知道究竟应该纠正到那一个数了。

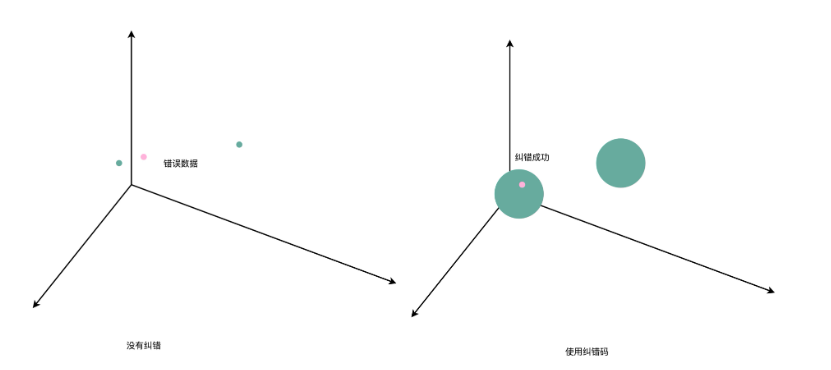
在没有纠错功能的情况下，我们看到的数据就好像是空间里面的一个一个点。这个时候，我们可以让数据之间的距离很紧凑，但是如果这些点的坐标稍稍有错，我们就可能搞错是哪一个点。

在有了 1 位纠错功能之后，就好像我们把一个点变成了以这个点为中心，半径为 1 的球。只要坐标在这个球的范围之内，我们都知道实际要的数据就是球心的坐标。而各个数据球不能距离太近，不同的数据球之间要有 3 个单位的距离。