目录
- 一、什么是Dijkstra算法
- 二、算法基本步骤
- 三、java代码
- 四、拓展(无向图的Dijkstra算法)
一、什么是Dijkstra算法
Dijkstra算法的核心思想是通过逐步逼近的方式,找出从起点到图中其他所有节点的最短路径。算法的基本步骤如下:
举个例子:
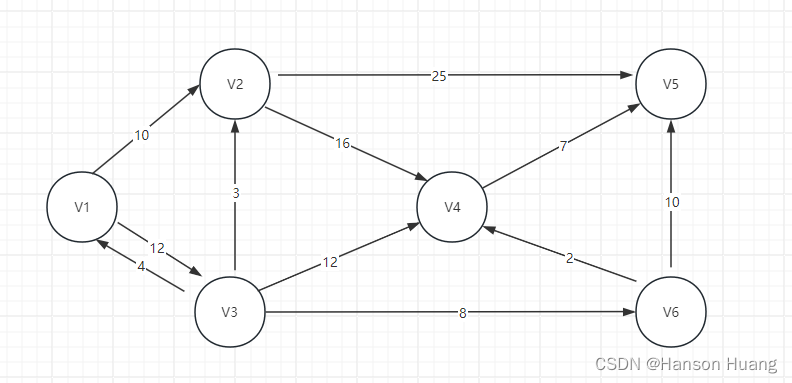
如图所示的V1-V6六个点及他们的有向权重连线,现在我们假设从V1点出发,画出从顶点V1到其余各点最短路径的过程:
首先,我们将V1拿出来,V1能通向V2和V3,V1到V1的距离我们可以看成0,V1到V2的距离是10,V1到V3的距离是12,V1不能直接到达V4,V5,V6,我们可以看成是无穷大,那么V1的上一个结点是V1,V2和V3的上一个结点也是V1。V4,V5,V6此是没有连接结点记为-1,得到如下表格
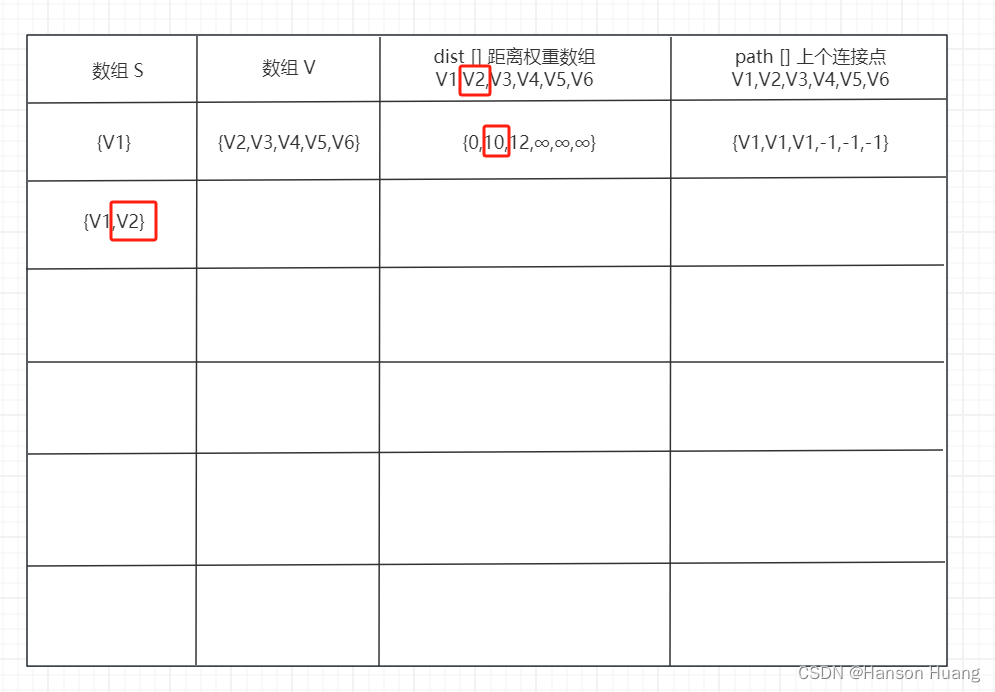
然后根据距离数组{0,10,12,∞,∞,∞},找出数组中距离最小的值,即V2的10,我们将V2拿出来放到数组S中,则数组V中还剩余{V3,V4,V5,V6},现在我们取出了V1,V2;V1到V1和V2的位置还是没有变,取出V2后,V1到V3没有新的通路,所以距离还是12,所以V3的上一个点还是V1;V4和V5是可以根据V2进行跟新的,V4=10+16=26,V5=10=25=35,我们取出了V1,V2,到V6还是没有路线可以走,所以更新之后的表格如下:
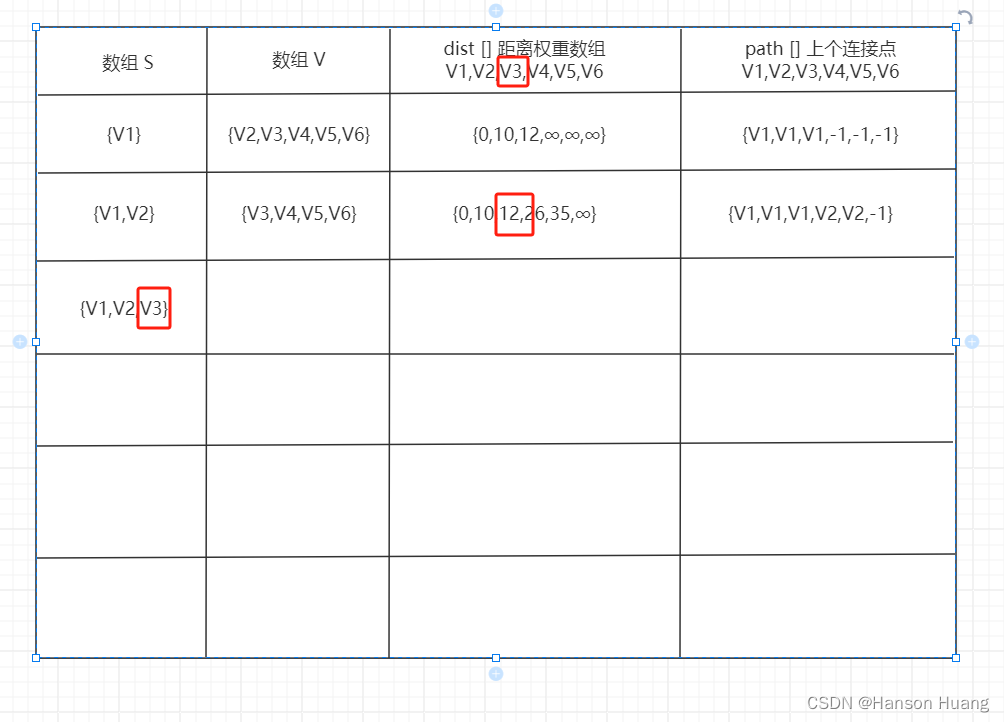
我们距离数组{0,10,12,26,35,∞}中,选取最小值,即12的V3结点加入数组S中,数组V为{V4,V5,V6},现在加入的结点为V1、V2、V3,现在V1到V2的路线多出来V1-V3-V2,但是总长度是15比原本的10要大啊,所以不做变化,V1到V3的距离还是12,V1-V4有两条路(V1-V2-V4)和(V1-V3-V4)跟新后的V1-V3-V4距离是24比原来的26更短,所以替换之,然后V4上一个点的坐标就变成了V3,我们再看一下V1-V5,(V1-V2-V5)和(V1-V3-V2-V5)显然还是原本的35是最短距离;V1-V6的路径是(V1-V3-V6)距离是20,更新表格:
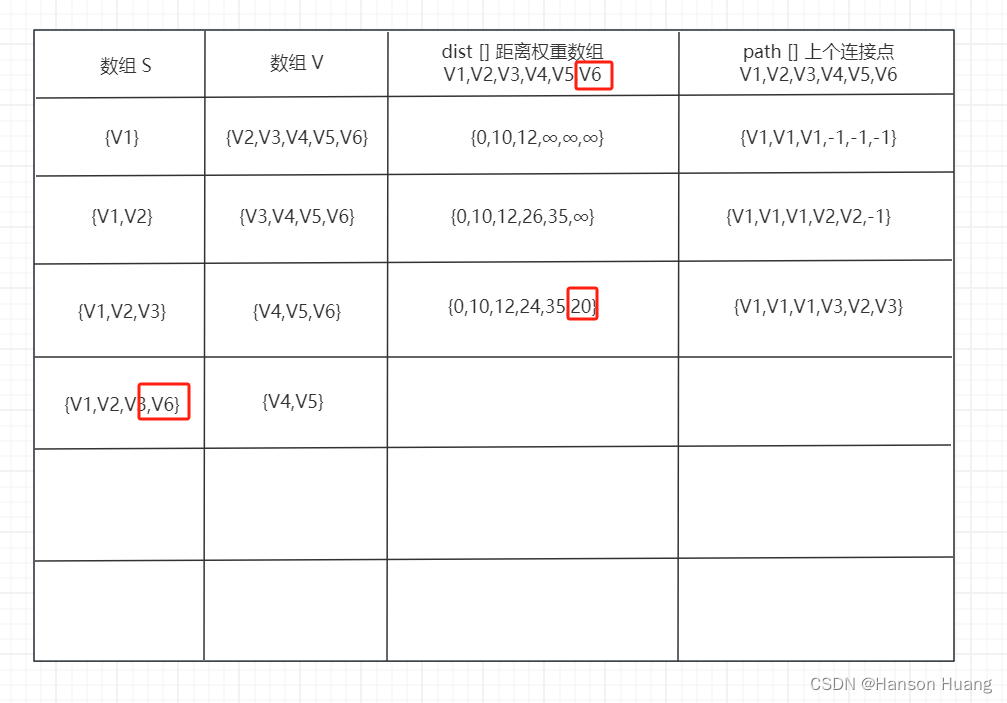
我们在数组{0,10,12,24,35,20}可以看出在去掉V1、V2、V3之后最小的点是V6的20,所以我们将V6加入到数组S中,V1到V1、V2、V3的距离保持不变;V1到V4的,因为增加了V6,所以多出来一条V1-V3-V6-V4,距离是22,比之前的24小,进行更新,所以V4的上一个结点变成V6;然后V1到V5,多增加路线V1-V3-V6-V5,总体距离变成30,比之前的35要小,更新表格,V5的上一个结点变成V6,跟新后的表格:

从数组V中取出距离最短的值V4放入数组S中,此时,V1到V1、V2、V3、V4的距离保持不变,V1-V5的距离多了一条V1-V3-V6-V4-V5,路径从29比以前的30要短,更新表格,所以V5的上一个结点的V4,V1-V6保持不变,更新后表格如下:
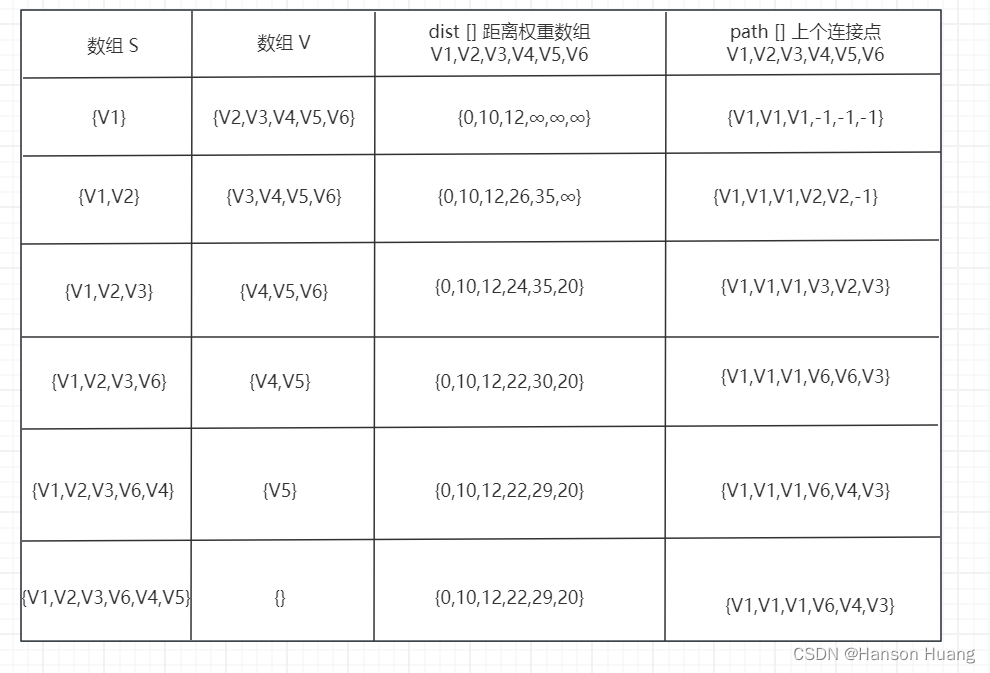
将最后一个点V5添加到数组S中,V5没有到其他点的新路径,所以dist[]和path[]数组不变。
如果想要知道V1到V6的距离:
先看path[],V6的上一个结点时V3,V3的上一个结点是V1,所以V1到V6的路径是V1-V3-V6;由dist[]数组得知距离权重是20;
如果想要知道V1到V5的距离:
先看path[],V5的上一个结点时V4,V4的上一个结点时V6,V6的上一个结点时V3,V3的上一个结点是V1,所以V1到V5的路径是V1-V3-V6-V4-V5;由dist[]数组得知距离权重是29;
其他的以此类推;
二、算法基本步骤
- 初始化:
- 创建一个最短路径信息数组shortPath[x][3],每一个一维数组含义为当前结点、该节点到此节点的最短路径、起始节点。
- 初始化shortPath数组,shortPath[x][0]当前节点编号、shortPath[x][1]最短路径、shortPath[x][2]起始结点编号
- 初始化优先队列,将起始节点的所有邻接点加入到优先队列中,结点信息使用Ownership类,属性值{time、nodeIndex、weight}。
- 创建优先队列,优先队列按照结点的权重值优先出队 PriorityQueue。
- 创建优先队列的比较器OwnershipCustomerComparator类,通过weight大小进行优先出队。
- 流程:
- 优先队列为空则退出
- 遍历优先队列,将队列中time版本对应的结点信息值写入shortPath中。每次拿到最新路径长度newWeight=matrix[up - 1][ownership.nodeIndex] + shortPath[up - 1][1](起始节点最短路径+起始节点到当前节点一条边的权重),如果当前结点未被初始化则直接将newWeight写入shortPath数组中,如果当前节点已经被写过最短路径,则直接略过当前newWeight即可,这里有一个dtx变量,记录当前优先队列中结点是否被写如果shortPath,用于time(版本)。
- 遍历优先队列(需要出队),将权重最小的结点出队,将该节点下的所有邻接点拿出做以下操作步骤:
- 需要是出对节点的邻接点
- 邻接点在shortPath表中的最短路径未被初始化(还是无穷大),将结点信息写入,最短路径为出对节点权重+出对节点到达该邻接点的权重
- 查看该邻接点是否出现在优先队列中。在优先队列中则更新shortPath数组以及优先队列中该结点的权重以及起始节点的信息。
- 优先队列中没有,Math.min(newWeight, shortPath[i][1]),取最优路径写入
三、java代码
代码地址:GitHub
算法代码:
public class Dijkstra {
private Queue visited;
int[] distance;
public Dijkstra(int len) {
// TODO Auto-generated constructor stub
visited = new LinkedList();
distance = new int[len];
}
private int getIndex(Queue q, int[] dis) {
int k = -1;
int min_num = Integer.MAX_VALUE;
for (int i = 0; i < dis.length; i++) {
if (!q.contains(i)) {
if (dis[i] < min_num) {
min_num = dis[i];
k = i;
}
}
}
return k;
}
public void dijkstra(int[][] weight, Object[] str, int v) {
HashMap path;
path = new HashMap();
for (int i = 0; i < str.length; i++)
path.put(i, "");
//初始化路径长度数组distance
for (int i = 0; i < str.length; i++) {
path.put(i, path.get(i) + "" + str[v]);
if (i == v)
distance[i] = 0;
else if (weight[v][i] != -1) {
distance[i] = weight[v][i];
path.put(i, path.get(i) + "-->" + str[i]);
} else
distance[i] = Integer.MAX_VALUE;
}
visited.add(v);
while (visited.size() < str.length) {
int k = getIndex(visited, distance);//获取未访问点中距离源点最近的点
visited.add(k);
if (k != -1) {
for (int j = 0; j < str.length; j++) {
//判断k点能够直接到达的点
if (weight[k][j] != -1) {
//通过遍历各点,比较是否有比当前更短的路径,有的话,则更新distance,并更新path。
if (distance[j] > distance[k] + weight[k][j]) {
distance[j] = distance[k] + weight[k][j];
path.put(j, path.get(k) + "-->" + str[j]);
}
}
}
}
}
for (int h = 0; h < str.length; h++) {
System.out.printf(str[v] + "-->" + str[h] + ":" + distance[h] + " ");
if (distance[h] == Integer.MAX_VALUE)
System.out.print(str[v] + "-->" + str[h] + "之间没有可通行路径");
else
System.out.print(str[v] + "-" + str[h] + "之间有最短路径,具体路径为:" + path.get(h).toString());
System.out.println();
}
visited.clear();
}
}
测试代码:
public static void main(String[] args) {
// TODO Auto-generated method stub
int[][] weight = {
{0, 10, 12, -1, -1, -1},
{-1, 0, -1, 16, 25, -1},
{4, 3, 0, 12, -1, 8},
{-1, -1, -1, 0, 7, -1},
{-1, -1, -1, -1, 0, -1},
{-1, -1, -1, 2, -1, 0}};
String[] str = {"V1", "V2", "V3", "V4", "V5", "V6"};
int len = str.length;
Dijkstra dijkstra = new Dijkstra(len);
//依次让各点当源点,并调用dijkstra函数
for (int i = 0; i < str.length; i++) {
dijkstra.dijkstra(weight, str, i);
}
}
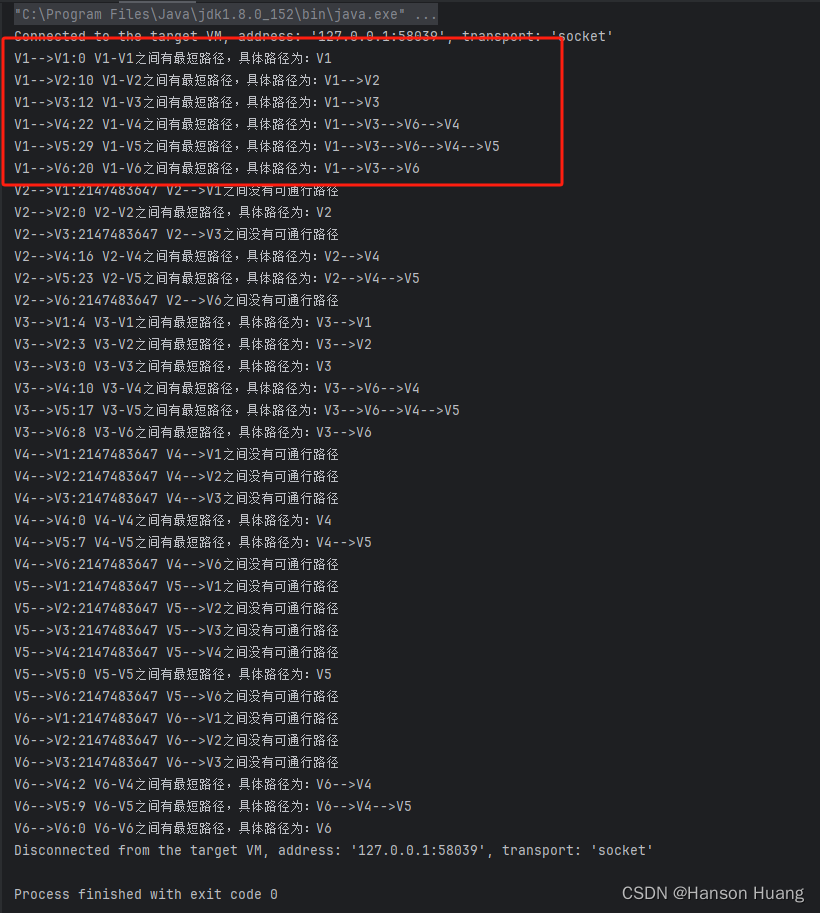
测试结果:
四、拓展(无向图的Dijkstra算法)
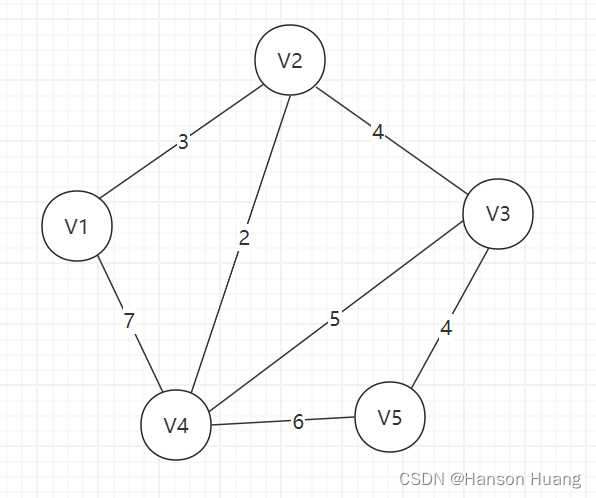
有向图问题解决了,无向图道理和有向图类似,例如如下的无向图,找出V1到其他个点的最短路径
我们只需要在Test类中定义一个无向图数组
int[][] undirected_weight = {
{0,3,-1,7,-1},
{3,0,4,2,-1},
{-1,4,0,5,4},
{7,2,5,0,6},
{-1,-1,4,6,0}};
String[] str = {"V1", "V2", "V3", "V4", "V5"};
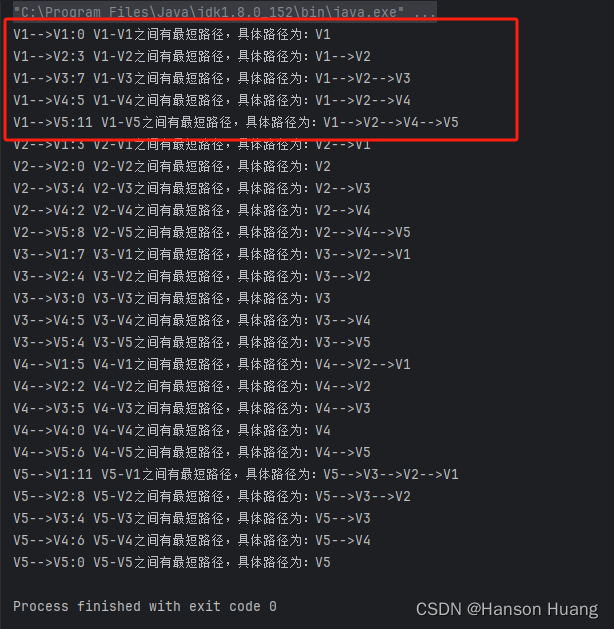
最后运行结果:
觉得有用的话还请多多点赞、收藏、评论!!!