2014年认证杯SPSSPRO杯数学建模
B题 位图的处理算法
原题再现:
图形(或图像)在计算机里主要有两种存储和表示方法。矢量图是使用点、直线或多边形等基于数学方程的几何对象来描述图形,位图则使用像素来描述图像。一般来说,照片等相对杂乱的图像使用位图格式较为合适,矢量图则多用于工程制图、标志、字体等场合。矢量图可以任意放缩,图形不会有任何改变。而位图一旦放大后会产生较为明显的模糊,线条也会出现锯齿边缘等现象。
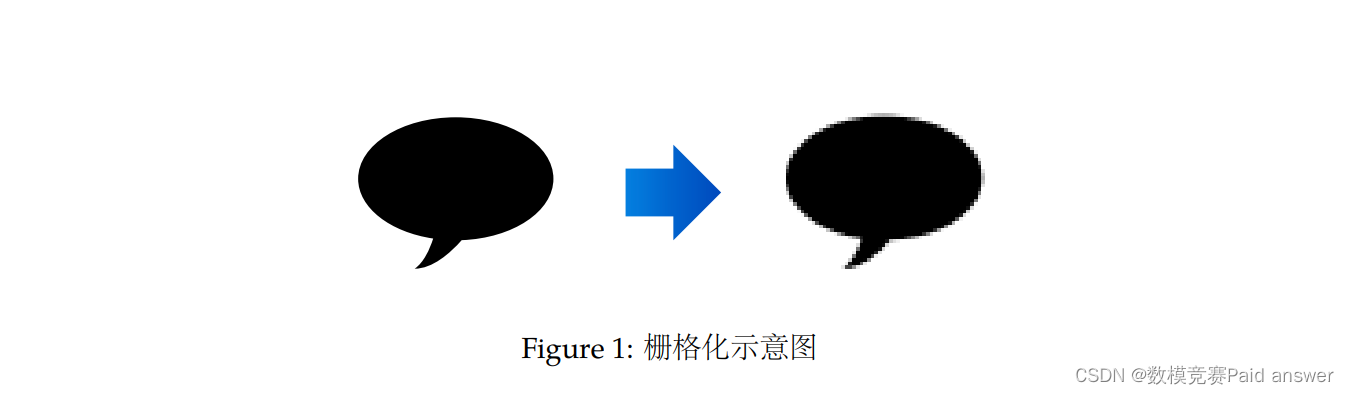
第一阶段问题: 矢量图从本质上只是使用曲线方程对图形进行的精确描述,在以像素为基本显示单元的显示器或打印机上是无法直接表现的。将矢量图转换成以像素点阵来表示的信息,再加以显示或打印,这个过程称之为栅格化(Rasterization),见图 1。
栅格化的逆过程相对比较困难。假设有一个形状较为简单的图标,保存成一定分辨率的位图文件。我们希望将其矢量化,请你建立合理的数学模型,尽量准确地提取出图案的边界线条,并将其用方程表示出来。
整体求解过程概述(摘要)
本次的问题是让我们处理栅格化逆过程,即根据位图图像像素点阵,得到矢量图形的几何特征,矢量图形本质上是使用曲线方程对图像进行精确描述,利用计算机辅助我们提取位图像素点阵特征,根据具体的拟合算法输出矢量图形。
首先,我们仔细分析图形信息,对图像进行了灰度处理,即对图像去彩色化。通过观察图像的灰度直方图,我们发现灰度直方图有双峰特性,采用 ostu 算法对图像进行了分割以及区域二值化,我们尝试了多种边缘检测算子,通过画图比较决定使用ostu+canny算子的方式进行边缘提取。从而得到边缘数据点。
然后,观察边缘数据点的分布情况,我们发现其在电脑内的存储状态没有构成点序列,出于对后面数据操作的便利,我们采用了 freeman 码的方式,对边界数据进行边缘跟踪,产生数据有序化,并在此过程中找出边界数据的突变点(尖点),为下一步的轮廓曲线拟合做准备。
接着,我们对有序化的边界数据进行了两种方式的拟合。第一种是采用抛物线样条曲线拟合,在之前的步骤中,我们得到了图形边界的尖点信息,由于整个图形是封闭的,我们以这些尖点作为分段点,在分段点区间内进行抛物线样条拟合,拟合标准便是所有点的偏差最小。从而得到边界轮廓方程。采取的第二种方法是针对于题目所给图像的特征,我们采取了分段函数拟合的办法,第一部分采用椭圆拟合的方式;第二部分是图形下部尖端部分,我们采用多项式拟合方式,最终得到边界图与边界方程。第一种方法具有一定的普适性,可以应用于任意形状的图形的拟合,拟合效果较为理想;第二种方法具有特殊性,针对有特定图像的拟合效果相对更好。
随后,在得到边界拟合曲线的基础上,我们综合比较了现在较为主流的种子填充算法和扫描线填充算法,并根据此次问题实际情况,提出了改进版本的扫描线填充算法,在进行边界内部填充的过程中,我们针对难填充的区域进行了区域划分,使得每一个区域都能够完美填充。
最后,我们考虑到图形程序较为复杂,与人的交互性较差,我们采用了简单的 matlab gui 界面方式对部分程序结果进行了统一展示,提高了程序的可视化以及人机交互性。
问题分析:
这次的问题是栅格化的逆过程,也即是从位图到矢量化图形的过程。由于位图计算机存储的是每个像素点的信息,而矢量图形计算机存储的是其几何特征。所以在栅格化逆过程中我们必须要考虑位图图像的几何特征,并想办法提取这些几何特征。对于一个封闭图形,我们如果能够知道图形的边界方程、线条的粗细以及颜色,那么我们最后的工作就是展现这些特征所标识的矢量图形。
图形的边界方程的获取一般会涉及边界区域的确定,进而得到边界数据点,并将数据点有序化。一般对于边界的拟合有多边形近似、样条插值拟合和分段函数拟合,而大部分拟合方法要求数据的有序化。
线条的粗细可以根据边界提取后的边界数据来确定,而颜色可以通过对于位图像素点的提取来确定。
模型假设:
假设 1:照片像素在 MATLAB 的处理范围内。
假设 2:填充的图形是封闭的,如果边缘本身有断点,用函数 bwfill 进行“补洞”操作;
假设 3:对于图片的比较微细小的部分,用膨胀函数 dilate 进行原图膨胀。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
function cl=clusterp(pic)
a=pic;
count=imhist(a);
[m,n]=size(a);
N=m*n;
L=256;
count=count/N;
for i=1:L
if count (i)~=0
st=i-1;
break;
end
end
for i=L:-1:1
if count (i)~=0
nd=i-1;
break;
end
end
F=count(st+1:nd+1);
p=st;
q=nd-st;
u=0;
for i=1:q
u=u+f(i)*(p+i-1);
ua(i)=u;
end;
for i=1:q
w(i)=sum(f(1:i));
end;
d=(u*w-ua).^2./(w.*(1-w));
[y,tp]=max(d);
th=tp+p;
for i=1:m
for j=1:n
if a(i,j)<th
a(i,j)=0;
else
a(i,j)=255;
end
end
end
imshow(a);
clear all
clc
F=imread('C:\Users\pc\Desktop\gui\图片1.png');
F1=rgb2gray(F);
F2=im2bw(F1);
m1=edge(F2,'canny');
m2=edge(F2,'sobel');
m3=edge(F2,'roberts');
m4=edge(F2,'log');
m5=bwperim(F2,4);
F=rgb2gray(F);
m6=F;
count=imhist(m6);
[m,n]=size(m6);
N=m*n;
L=256;
count=count/N;
for i=1:L
if count(i)~=0
st=i-1;
break;
end
end
for i=L:-1:1
if count(i)~=0
nd=i-1;
break;
end
end
f=count(st+1:nd+1);
p=st;
q=nd-st;
u=0;
for i=1:q
u=u+f(i)*(p+i-1);
ua(i)=u;
end;
for i=1:q
w(i)=sum(f(1:i));
end;
d=(u*w-ua).^2./(w.*(1-w));
[y,tp]=max(d);
th=tp+p;
for i=1:m
for j=1:n
if m6(i,j)<th
m6(i,j)=0;
else
m6(i,j)=255;
end
end
end
subplot(2,2,2);
imshow(m6);
subplot(2,2,3);m6=edge(m6,'canny');
imshow(m6);
m11=imcomplement(m1);
m21=imcomplement(m2);
m31=imcomplement(m3);
m41=imcomplement(m4);
m51=imcomplement(m5);
[L,W]=size(m51);
m51(:,1)=1;m51(:,W)=1;m51(1,:)=1;m51(L,:)=1;
m61=imcomplement(m6);
subplot(2,3,1),imshow(m11),title('canny算子')
subplot(2,3,2),imshow(m21),title('sobel算子')
subplot(2,3,3),imshow(m31),title('roberts算子')
subplot(2,3,4),imshow(m41),title('log算子')
subplot(2,3,5),imshow(m51),title('bwperim')
subplot(2,3,6),imshow(m61),title('ostu+canny算子')