计算机网络——27路由选择算法

路由选择算法

路由协议

路由协议的目标：确定从发送主机到接收主机之间，通过路由器的网络“较好”的路径（等价于路由器的序列）

路径：路由器的序列，分组将会沿着该序列从源主机到达最后的目标主机
“较好”：最小“代价”，“最快的”，“最不拥塞”
路由：一个“top-10”网络挑战

路由的概念

路由：按照某种指标（传输延迟，所经过的站点数目等）找到一条从源节点到目标节点的较好路径
- 较好路径：按照某种指标较小的路径
- 指标：站数、延迟、费用，队列长度等，或者是一些单纯指标的加权平均
- 采用什么样的指标，表示网络使用者希望网络在什么方面表现突出，什么指标网络使用者比较重视
路由器 - 路由器之间的最优路径 = 主机对之间的最优路径
- 路由器连接子网，子网到路由器之间的跳数就一跳，必须要走
- 路由器到下一跳路由器（节点到节点）之间的最优路径找到了
- 也就找到了从源子网向目标子网所有主机对之间的最优路径
- 大大降低了路由计算的规模
- 在路由计算中按照子网到子网的路径计算为目标，而不是主机到主机
路由选择算法：网络层软件的一部分，完成路由功能

网络的图抽象

图抽象

在这里插入图片描述

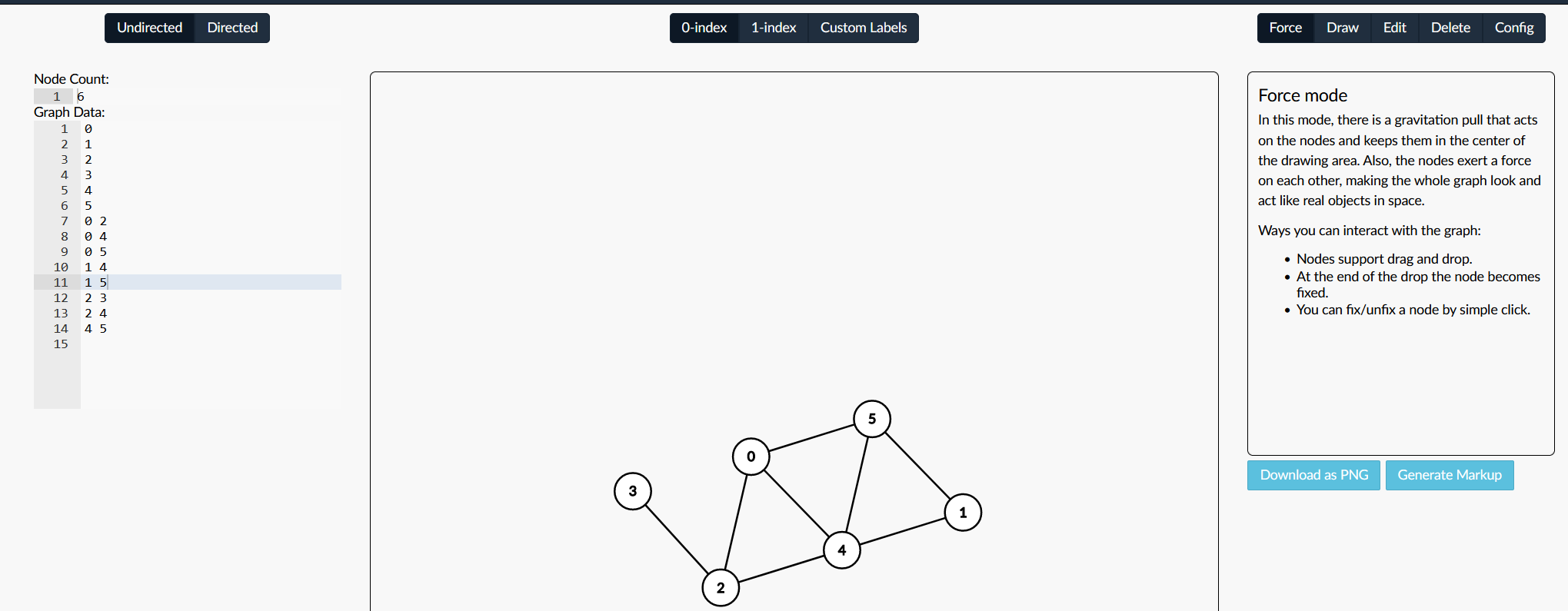
图：G = (N,E)
N = 路由集合器 = (u,v,w,x,y,z)
E = 链路集合 = ((u,v),(u,x),(v,x),(v,w),(x,w),(x,y),(w,y),(w,z),(y,z)) 边有代价

边和路径的代价

c(x,x’) = 链路的代价(x,x’)
代价可能总为1
或是链路带宽的倒数
或是拥塞情况的倒数
cost of path( $x_1,x_2,x_3,...,x_p$ ) = c( $x_1,x_2$ ) + c( $x_2,x_3$ ) + … + c( $x_{p-1},x_p$ )

最优化原则

汇集树

此节点到所有其他节点的最优路径形成的树
路由选择算法就是为所有路由器找到并使用汇集树

在这里插入图片描述

路由的原则

路由选择算法的原则

正确性：算法必须是正确的和完整的，使分组一站一站接力，正确发向目标站；完整：目标所有的站地址，在路由表中都能找到相应的表项；没有处理不了的目标站地址
简单性：算法在计算机上应简单：最优但复杂的算法，时间上延迟很大，不实用，不应为了获取路由信息增加很多的通信量
健壮性：算法应能适应通信量和网络拓扑的变化：通信量变化，网络拓扑的变化算法能很快适应；不向很拥挤的链路发送数据，不向断了的链路发送数据
稳定性：产生的路由不应该摇摆
公平性：对每一个站点都公平
最优性：某一个指标的最优，时间上，费用上等指标，或综合指标；实际上，获取最优的结果代价较高，可能是次优的

路由算法分类

全局或局部路由信息
全局：

所有的路由器拥有完整的拓扑和边的代价的信息
"link state"算法

分布式：

路由器只知道与它有物理连接关系的邻居路由器，和到相应邻居路由器的代价值
迭代地与邻居交换路由信息，计算路由信息
"**distance vector"算法

静态或动态
静态：

路由随时间变化缓慢

动态：

路由变化很快
- 周期性更新
- 根据链路代价的变化而变化

链路静态路由（LS）

LS路由的工作过程

配置LS路由选择算法的路由工作过程

各点通过各种渠道获得整个网络拓扑，网络中所有链路代价等信息（这部分和算法没关系，属于协议和实现）
使用LS路由算法，计算本站点到其他站点的最优路径（汇集树），得到路由表
按照此路由表转发分组(datagram方式)
- 严格意义上说不是路由的一个步骤
- 分发到输入端口的网络层

LS路由的基本工作过程

发现相邻节点，获知对方网络地址
测量到相邻节点的代价（延迟、开销）
组装一个LS分组，描述它到相邻节点的代价情况
将分组通过扩散的方式发到所有其他路由器
- 以上四步让每个路由器获得拓扑和边代价
通过Dijkstra算法找出最短路径（这才是路由算法）
- 每个节点独立算出来到其他节点（路由器 = 网络）的最短路径
- 迭代算法：第k步能够知道本节点到k个其他节点的最短路径

链路状态路由选择

发现相邻节点，获知对方网络地址
- 一个路由器上电之后，向所有线路发送Hello分组
- 其他路由器接收到Hello分组，回送应答，在应答分组中，告知自己的名字（全局唯一）
- 在LAN中，通过广播Hello分组，获得其他路由器的信息，可以认为引入一个人工节点

在这里插入图片描述

测量到相邻节点的代价（延迟、开销）
- 实测法，发送一个分组要求对方立即响应
- 回送一个ECHO分组
- 通过测量时间可以估算出延迟情况
组装一个分组，描述相邻节点的情况
- 发送者名称
- 序号，名称
- 列表：给出他相邻节点，和它到相邻节点的延迟

在这里插入图片描述

将分组通过扩散的方法发送到所有其他路由器
- 序列号：用于控制无穷的扩散，每个路由器都记录（源路由号，顺序号），发现重复的或老的就不扩散
  - 具体问题1：循环使用问题
  - 具体问题2：路由器崩溃之后序号从0开始
  - 具体问题3：序号出现错误
- 解决问题的方法：年龄字段
  - 生成一个分组时，年龄字段不为0
  - 每一个时间段，AGE字段减一
  - AGE字段为0的分组将被抛弃
- 关于扩散分组的数据结构
  - Source：从哪个节点收到LS分组
  - Seq,Age：序号，年龄
  - Send flags：发送标记，必须向指定的哪些相邻站点转发LS分组
  - ACK flags：本站点必须向哪些相邻站点发送应答
  - DATA：来自source站点的LS分组
  - 节点B的数据结构

Source	Seq	Age	Send flags A	Send flags C	Send flags F	ACK flags A	ACK flags C	ACK flags F
A(相邻)	21	60(初始TTL)	0	1	1	1(A与B相邻，直接获取A的分组，给A ACK)	0	0
F(相邻)	21	60	1	1	0	0	0	1
E(通过A、F获取)	21	59(一次hop)	0	1	0	1(E通过A获取，给A ACK)	0	1
C(相邻)	20	60	1	0	1	0	1	0
D(通过C、F获取)	21	59	1	0	0	0	1	1

通过Dijkstra算法找出最短路径
- 路由器获得各站点LS分组和整个网络的拓扑
- 通过Dijkstra算法计算出到其他服务器的最短路径（汇集树）
- 将计算结果安装到路由表中

LS的应用情况

OSPF协议是一种LS协议，被用于Internet上
IS-IS(intermediate system - intermediate system)：被用于Internet主干中，Netware

Dijkstra算法

符号标记

c(i,j)：从节点i到j链路代价（初始状态下非相邻节点之间的链路代价为∞）
D(v)：从源节点到节点V的当前路径代价（节点的代价）
p(v)：从源到节点V的路径前序节点
N’：当前已经知道最优路径的节点集合（永久节点的集合）

在这里插入图片描述

LS路由选择算法的工作原理

节点标记：每一个节点使用(D(v),p(v))标记

D(v)从源节点由已知最优路径到达本节点的距离
P(v)前序节点来标注

2类节点

临时节点：还没有找到从源节点到此节点的最优路径的节点
永久节点 N’：已经找到了从源节点到此节点的最优路径的节点

算法具体流程

初始化
- 除了源节点外，所有节点都为临时节点
- 节点代价除了与源节点代价相邻的节点外，都为∞
从所有临时节点中找到一个节点代价最小的临时节点，将之变为永久节点（当前结点）W
对此节点的所有在临时节点集合中的邻节点(V)
- 如 D(v)>D(w) + c(w,v), 则重新标注此点, (D(W)+C(W,V), W)
- 否则，不重新标注
开始一个新的循环

例子

在这里插入图片描述

Dijkstra例子

在这里插入图片描述

Dijkstra算法的讨论

算法复杂度: n节点

每一次迭代: 需要检查所有不在永久集合N中节点
n(n+1)/2 次比较: O(n2 )
有很有效的实现: O(nlogn)

可能会出现震荡问题：

例如：链路代价 = 链路承载的流量
路径改变次数过多

在这里插入图片描述

距离矢量路由选择

基本思想

各路由器维护一张路由表，结构如图

To(目标)	Next(到达目标的代价最小的路径中，下一跳)	cost(到目标的代价)
A	Z	14
…	…	…

各路由器与相邻路由器交换路由表(待续)
根据获得的路由信息,更新路由表(待续)

在这里插入图片描述

代价及相邻节点间代价的获得
- 跳数(hops), 延迟(delay),队列长度
- 相邻节点间代价的获得：通过实测
路由信息的更新
- 根据实测得到本节点A到相邻站点的代价（如:延迟）
- 根据各相邻站点声称它们到目标站点B的代价，计算出本站点A经过各相邻站点到目标站点B的代价
- 找到一个最小的代价，和相应的下一个节点Z，到达节点B经过此节点Z，并且代价为A-Z-B的代价
- 其它所有的目标节点同样的计算方法

在这里插入图片描述

例子1

以当前节点J为例,相邻节点 A,I,H,K
J测得到A,I,H,K的延迟为 8ms,10ms,12ms,6ms
通过交换DV, 从A,I,H,K获得到它们到G的延迟为 18ms,31ms,6ms,31ms
因此从J经过A,I,H,K到G的延迟为26ms(8 + 18),41ms(10 + 31),18ms(12 + 6), 37ms(31 + 6)
将到G的路由表项更新为18ms, 下一跳为：H(18ms对应的节点)
其它目标一样，除了本节点J

在这里插入图片描述

DV的无穷计算问题

DV的特点
- 好消息传的快，坏消息传的慢
好消息的传播以每一个交换周期前进一个路由器的速度进行
- 好消息：某个路由器接入或有更短的路径
- 举例
坏消息的传播速度非常慢(无穷计算问题)

在这里插入图片描述

例子:
- AB之间断开了
- 第一次交换之后, B从C处获得信息,C可以到达A(C-A, 要经过B本身),但是路径是2,因此B变成3,从C处走
- 第二次交换,C从B处获得消息, B可以到达A,路径为3, 因此,C到A从B走,代价为3（因为每次改变都会向周围传递Dv ）
- 无限此之后, 到A的距离变成INF,不可达

在这里插入图片描述

Bellman-Ford 方程（动态规划）

设 dx(y) := 从x到y的最小路径代价，那么 dx(y) = min {c(x,v) + dv(y) }
其中：v是x的邻居

例子

在这里插入图片描述

明显的,
$d_v(z) = 5, d_x(z) = 3, d_w(z) = 3$
由于B-F方程得到：
$d_u(z) = min \{ c(u,v) + d_v(z), c(u,x) + d_x(z), c(u,w) + d_w(z) \} = min \{2 + 5, 1 + 3, 5 + 3\} = 4$

那个能够达到目标z最小代价的节点x，就在到目标节点的下一条路径上, 在转发表中使用

思路

$D_x(y)$ = 节点x到y代价最小值的估计

x 节点维护距离矢量 $D_x = [D_x (y): y ∈ N ]$

节点x:

知道到所有邻居v的代价: c(x,v)
收到并维护一个它邻居的距离矢量集
对于每个邻居, x 维护 $D_v = [D_v (y): y є N]$

核心思路

每个节点都将自己的距离矢量估计值传送给邻居，定时或者DV有变化时，让对方去算
当x从邻居收到DV时，自己运算，更新它自己的距离矢量（采用B-F equation）
$D_x(y) ← min_v\{c(x,v) + D_v(y)\}$ 对于每个节点y ∈ N
X往y的代价x到邻居v代价v声称到y的代价
Dx(y)估计值最终收敛于实际的最小代价值 $d_x(y)$

特点

异步式,迭代: 每次本地迭代被以下事件触发:

本地链路代价变化了
从邻居来了DV的更新消息

分布式:

每个节点只是在自己的DV改变之后向邻居通告
然后邻居们在有必要的时候通知他们的邻居

在这里插入图片描述

水平分裂(split horizon)算法

一种对无穷计算问题的解决办法 —— 结局坏消息传的慢的问题

当AB断开之后，C进行交换
C知道要经过B才能到达A，所以C向B报告它到A的距离为INF；C 告诉D它到A的真实距离2（就这样一边传递INF，一边传递真实举例2，水平方向分裂）
下一阶段，C发现到A的路径断开了，D进行交换
D告诉E,它到A的距离,但D告诉C它通向A的距离为INF
第一次交换: B通过测试发现到A的路径为INF,而C也告诉B到A的距离为INF,因此,B到A的距离为INF
第二次交换: C从B和D那里获知,到A的距离为INF,因此将它到A的距离为INF
……坏消息以一次交换一个节点的速度传播

在这里插入图片描述

水平分裂算法问题

水平分裂的问题:在某些拓扑形式下会失败（存在环路）

在这里插入图片描述

A,B到D的距离为2, C到D的距离为1
如果C-D路径失败
C获知到D为INF,从A,B获知到D的距离为INF,因此C认为D不可达
A从C获知D的距离为INF,但从B处获知它到D的距离为2,因此A到B的距离为3,从B走
B也有类似的问题
经过无限次之后,A和B都知道到D的距离为INF

在这里插入图片描述

例子

在这里插入图片描述

LS和DV算法的比较

消息复杂度（DV胜出） O(NE)
收敛时间（LS胜出） O(NlogN)
健壮性（LS胜出）节点之间影响较小

性能指标	LS特点	DV特点	比较结果
消息复杂度	有n 节点, E 条链路,发送报文O(nE)个；（局部的路由信息；全局传播）	只和邻居交换信息（全局的路由信息，局部传播）	DV胜出
收敛时间	O( $n^2$ ) 算法；有可能震荡	收敛较慢；可能存在路由环路；count-to-infinity 问题	LS胜出
健壮性(路由器故障会发生什么)	节点会通告不正确的链路代价,每个节点只计算自己的路由表,错误信息影响较小，局部，路由较健壮	节点可能通告对全网所有节点的不正确路径代价,每一个节点的路由表可能被其它节点使用,错误可以扩散到全网	LS胜出