102. 二叉树的层序遍历,104. 二叉树的最大深度,110. 平衡二叉树,每题做详细思路梳理,配套Python&Java双语代码, 2024.03.25 可通过leetcode所有测试用例。
目录
102. 二叉树的层序遍历
解题思路
完整代码
Java
Python
104. 二叉树的最大深度
解题思路
完整代码
Java
Python
110. 平衡二叉树
解题思路
完整代码
Java
Python
102. 二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。示例 1:
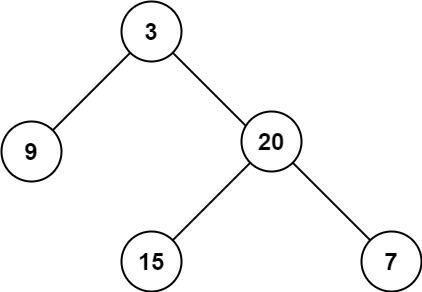
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-1000 <= Node.val <= 1000
解题思路
要解决这个问题,我们可以使用广度优先搜索(BFS)策略。这个策略适合层序遍历,因为它先访问离根节点近的节点,然后再访问离根节点远的节点。具体到二叉树的层序遍历,我们可以按照以下步骤进行:
- 初始化一个队列,将根节点入队。
- 当队列不为空时,进行循环:
- 记录当前队列的大小,这个大小即为当前层的节点数。
- 依次处理当前层的每个节点:将节点从队列中移除,并记录其值;然后按照从左到右的顺序,将其非空子节点入队。
- 将当前层的节点值列表加入最终结果中。
- 当队列为空时,所有节点已访问完毕,返回最终结果。
完整代码
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int levelSize = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < levelSize; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
result.add(level);
}
return result;
}
}Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
result, queue = [], [root]
while queue:
level_size = len(queue)
level = []
for _ in range(level_size):
node = queue.pop(0)
level.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(level)
return result104. 二叉树的最大深度
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:3示例 2:
输入:root = [1,null,2] 输出:2
解题思路
为了解决这个问题,我们可以采用递归的方法来计算二叉树的最大深度。具体的思路如下:
- 基础情况:如果当前节点为空,即到达了叶子节点的下一个位置,返回深度为0。
- 递归计算:对当前节点的左右子树分别递归调用函数计算其最大深度。
- 合并结果:当前节点的最大深度等于其左右子树最大深度的较大者加1(加的这个1代表当前节点这一层)。
完整代码
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
// 基础情况:空节点的深度为0
if (root == null) {
return 0;
}
// 递归计算左右子树的最大深度
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
// 当前节点的最大深度是左右子树的最大深度的较大者加1
return Math.max(leftDepth, rightDepth) + 1;
}
}Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
# 基础情况:如果当前节点为空,则返回深度0
if not root:
return 0
# 递归计算左子树的最大深度
left_depth = self.maxDepth(root.left)
# 递归计算右子树的最大深度
right_depth = self.maxDepth(root.right)
# 当前节点的最大深度为左右子树的最大深度的较大值加1
return max(left_depth, right_depth) + 1110. 平衡二叉树
给定一个二叉树,判断它是否是
平衡二叉树
示例 1:
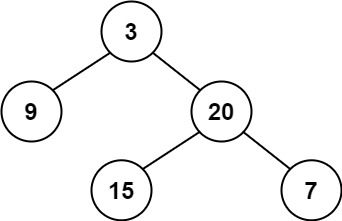
输入:root = [3,9,20,null,null,15,7] 输出:true示例 2:
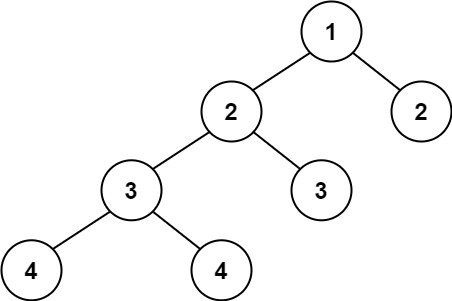
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false示例 3:
输入:root = [] 输出:true
解题思路
判断一个二叉树是否是平衡二叉树,我们需要了解平衡二叉树的定义:一个二叉树如果每个节点的左右两个子树的高度差的绝对值不超过1,那么它就是平衡二叉树。基于这个定义,我们可以采用递归的方法来解决这个问题,具体思路如下:
-
递归函数的目的:编写一个辅助函数,该函数返回两个信息:当前子树是否平衡,以及当前子树的高度。
-
基础情况:如果当前节点为空,那么这个子树自然是平衡的,高度为0。
-
递归逻辑:
- 对当前节点的左子树调用递归函数,获取左子树是否平衡以及左子树的高度。
- 对当前节点的右子树调用递归函数,获取右子树是否平衡以及右子树的高度。
- 如果左右子树都是平衡的,并且左右子树的高度差的绝对值不超过1,则当前子树是平衡的。当前子树的高度是左右子树的高度的较大值加1。
-
终止条件:如果在任何时候发现子树不平衡,则可以立即停止进一步的递归,因为不需要再检查其他部分了。
完整代码
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return check(root).isBalanced;
}
private TreeInfo check(TreeNode node) {
if (node == null) {
return new TreeInfo(true, 0);
}
TreeInfo left = check(node.left);
TreeInfo right = check(node.right);
boolean isBalanced = left.isBalanced && right.isBalanced && Math.abs(left.height - right.height) <= 1;
int height = 1 + Math.max(left.height, right.height);
return new TreeInfo(isBalanced, height);
}
class TreeInfo {
boolean isBalanced;
int height;
TreeInfo(boolean isBalanced, int height) {
this.isBalanced = isBalanced;
this.height = height;
}
}
}Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
def check(node):
if not node:
return True, 0
leftBalanced, leftHeight = check(node.left)
rightBalanced, rightHeight = check(node.right)
# 当前子树是否平衡,以及当前子树的高度
return (leftBalanced and rightBalanced and abs(leftHeight - rightHeight) <= 1,
1 + max(leftHeight, rightHeight))
return check(root)[0]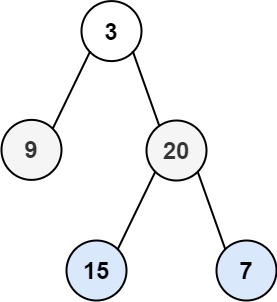




![[NKCTF 2024]web解析](https://img-blog.csdnimg.cn/direct/30d11b0ba6c145d9819bf9d169a944eb.png)