在这个实验室里，我们将探索softmax函数。当解决多类分类问题时，该函数用于Softmax回归和神经网络。

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from IPython.display import display, Markdown, Latex
from sklearn.datasets import make_blobs
%matplotlib widget
from matplotlib.widgets import Slider
from lab_utils_common import dlc
from lab_utils_softmax import plt_softmax
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)

注：通常，在本课程中，笔记本使用以0开始计数，以N-1结束计数的约定，∑𝑁−1.𝑖=0
，而讲座以1开始，以N结束，∑𝑁𝑖=1.
这是因为代码通常会以0开始迭代，而在讲座中，从1到N计数会产生更干净、更简洁的方程。这本笔记本的方程式比实验室的典型方程式多，因此将打破惯例，从1到N计数。

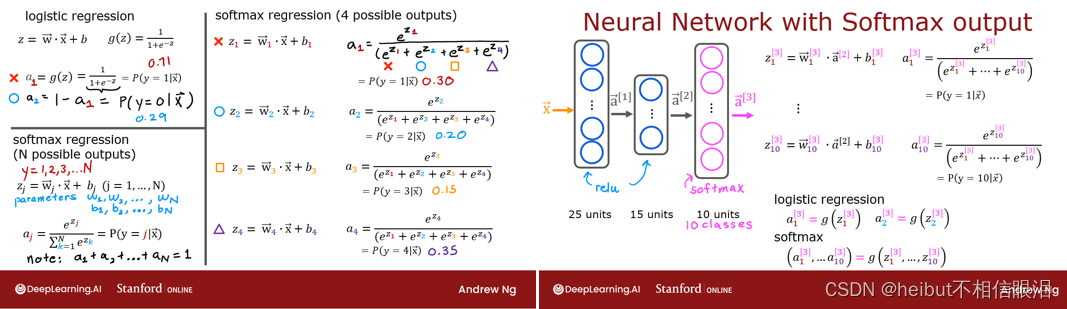
Softmax函数
在具有Softmax输出的Softmax回归和神经网络中，生成N个输出，并选择一个输出作为预测类别。在这两种情况下，矢量𝐳由应用于softmax函数的线性函数生成。softmax功能转换𝐳
转换成如下所述的概率分布。在应用softmax之后，每个输出将在0和1之间，并且输出将加1，使得它们可以被解释为概率。较大的输入将对应于较大的输出概率。


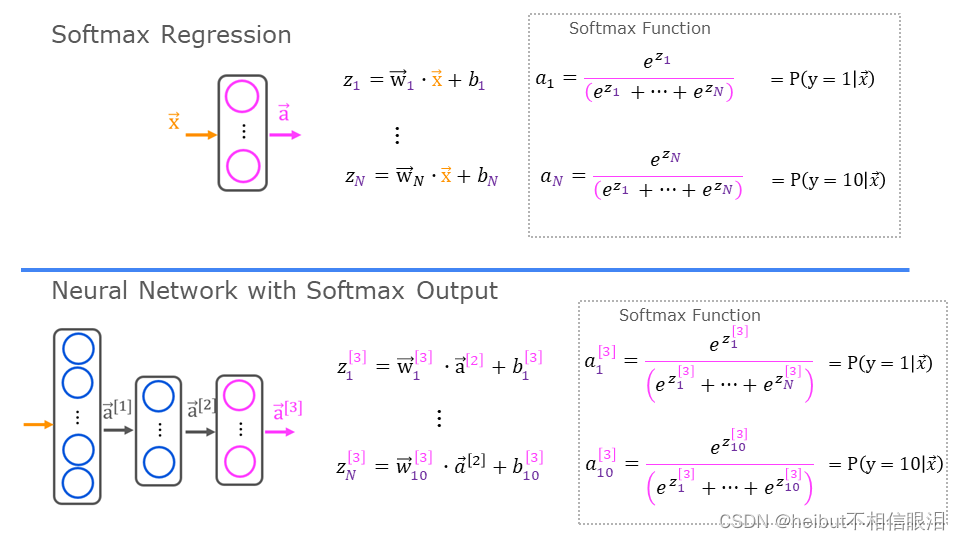
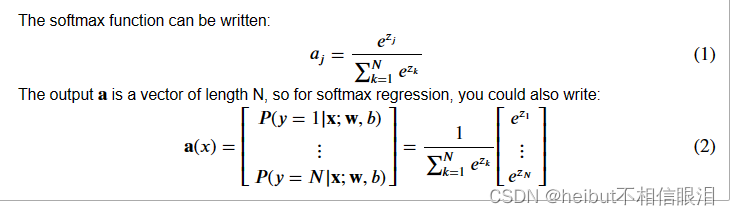
这表明输出是一个概率向量。第一个条目是输入是给定输入的第一个类别的概率𝐱
和参数𝐰和𝐛.让我们创建一个NumPy实现：

def my_softmax(z):
    ez = np.exp(z)              #element-wise exponenial
    sm = ez/np.sum(ez)
    return(sm)

下面，使用滑块更改z输入的值。

plt.close("all")
plt_softmax(my_softmax)

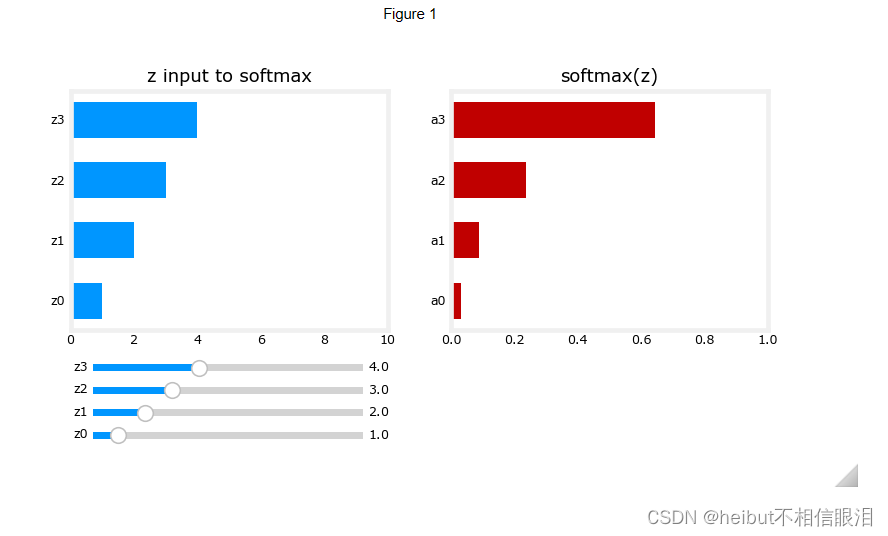
图1当您改变上述z的值时，需要注意以下几点：

• softmax分子中的指数放大了数值中的微小差异
• 输出值总和为1
• softmax跨越所有输出。例如，z0的变化将改变a0-a3的值。将其与具有单个输入和单个输出的ReLu或Sigmoid等其他激活进行比较。

Cost

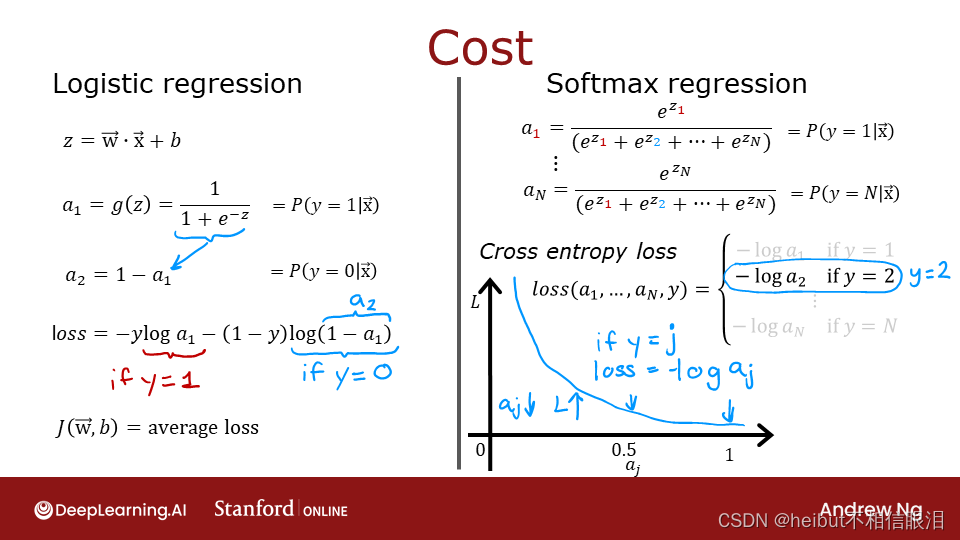
与Softmax相关的损失函数，即交叉熵损失，为：

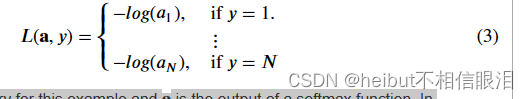
其中y是本例的目标类别，𝐚是softmax函数的输出。特别是中的值𝐚是总和为1的概率。

回想一下：在本课程中，损失是一个例子，而成本涵盖了所有例子。

注意，在上面的（3）中，只有与目标相对应的线对损失有贡献，其他线为零。为了编写成本方程，我们需要一个“指标函数”，当指数与目标匹配时，该函数为1，否则为零。

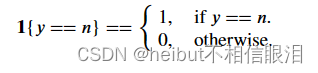
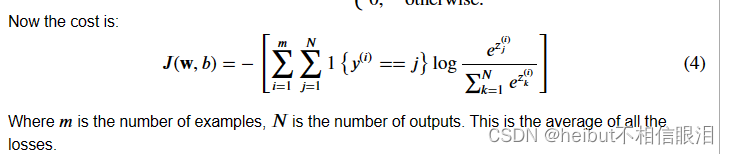
Tensorflow

本实验室将讨论两种实现softmax的方法，Tensorflow中的交叉熵损失，“明显”方法和“首选”方法。前者是最直接的，而后者在数值上更稳定。
让我们首先创建一个数据集来训练多类分类模型。

# make  dataset for example
centers = [[-5, 2], [-2, -2], [1, 2], [5, -2]]
X_train, y_train = make_blobs(n_samples=2000, centers=centers, cluster_std=1.0,random_state=30)

显而易见的组织
下面的模型是用softmax作为最终致密层中的激活来实现的。loss函数在compile指令中单独指定。
损失函数稀疏类别交叉熵。上述（3）中所述的损失。在这个模型中，softmax发生在最后一层。损失函数采用softmax输出，softmax输出是概率的向量。

model = Sequential(
    [ 
        Dense(25, activation = 'relu'),
        Dense(15, activation = 'relu'),
        Dense(4, activation = 'softmax')    # < softmax activation here
    ]
)
model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(0.001),
)

model.fit(
    X_train,y_train,
    epochs=10
)
        

因为softmax被集成到输出层中，所以输出是概率的向量

p_nonpreferred = model.predict(X_train)
print(p_nonpreferred [:2])
print("largest value", np.max(p_nonpreferred), "smallest value", np.min(p_nonpreferred))

63/63 [==============================] - 0s 1ms/step
[[3.74e-03 2.83e-03 9.64e-01 2.92e-02]
 [9.96e-01 4.21e-03 1.13e-05 7.58e-05]]
largest value 0.9999949 smallest value 1.9021733e-09

Preferred
回想一下讲座，如果在训练中结合softmax和loss，可以获得更稳定、更准确的结果。这是由此处显示的“首选”组织启用的。

在优选的组织中，最后一层具有线性激活。由于历史原因，这种形式的输出被称为logits。loss函数还有一个额外的参数：from_logits=True。这会通知损失函数softmax操作应包含在损失计算中。这允许优化实现。

preferred_model = Sequential(
    [ 
        Dense(25, activation = 'relu'),
        Dense(15, activation = 'relu'),
        Dense(4, activation = 'linear')   #<-- Note
    ]
)
preferred_model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),  #<-- Note
    optimizer=tf.keras.optimizers.Adam(0.001),
)

preferred_model.fit(
    X_train,y_train,
    epochs=10
)
        

输出处理
注意，在首选模型中，输出不是概率，而是从大负数到大正数的范围。当执行预期概率的预测时，必须通过softmax发送输出。让我们来看看首选的模型输出：

p_preferred = preferred_model.predict(X_train)
print(f"two example output vectors:\n {p_preferred[:2]}")
print("largest value", np.max(p_preferred), "smallest value", np.min(p_preferred))

63/63 [==============================] - 0s 1ms/step
two example output vectors:
 [[-0.26 -1.67  3.39 -0.25]
 [ 6.5   1.12 -2.74 -2.4 ]]
largest value 12.235959 smallest value -9.061906

输出预测不是概率！如果期望的输出是概率，则该输出应通过softmax进行处理。

sm_preferred = tf.nn.softmax(p_preferred).numpy()
print(f"two example output vectors:\n {sm_preferred[:2]}")
print("largest value", np.max(sm_preferred), "smallest value", np.min(sm_preferred))

two example output vectors:
 [[2.47e-02 6.04e-03 9.44e-01 2.48e-02]
 [9.95e-01 4.61e-03 9.66e-05 1.35e-04]]
largest value 0.999998 smallest value 5.6292937e-10

要选择最可能的类别，不需要softmax。可以使用np.argmax（）找到最大输出的索引。

for i in range(5):
    print( f"{p_preferred[i]}, category: {np.argmax(p_preferred[i])}")

[-0.26 -1.67  3.39 -0.25], category: 2
[ 6.5   1.12 -2.74 -2.4 ], category: 0
[ 4.89  1.43 -1.95 -1.89], category: 0
[-0.4   5.31 -0.04 -0.4 ], category: 1
[ 1.22 -1.58  6.53 -1.76], category: 2

稀疏类别交叉熵或类别交叉熵

Tensorflow有两种潜在的目标值格式，损失的选择定义了预期值。
SparseCategorialCrossentropy：期望目标是与索引相对应的整数。例如，如果有10个潜在的目标值，y将在0和9之间。
类别交叉熵：期望示例的目标值是一个热编码的值，其中目标索引处的值为1，而其他N-1个条目为零。一个具有10个潜在目标值的示例（其中目标为2）为[0,0,1,0,0,0,0]。

祝贺

在这个实验室里，你

• 越来越熟悉softmax函数及其在softmax回归和神经网络中的softmax激活中的应用。
• 在Tensorflow中学习了首选的模型构建：
  • 最后一层没有激活（与线性激活相同）
  • 稀疏类别交叉熵损失函数
  • use from_logits=True
• 认识到与ReLu和Sigmoid不同，softmax跨越多个输出。