Probabilistic Imputation for Time-series Classification with Missing Data

论文链接：https://icml.cc/virtual/2023/poster/23522

作者：SeungHyun Kim · Hyunsu Kim · EungGu Yun · Hwangrae Lee · Jaehun Lee · Juho Lee

机构：韩国科学技术院（KAIST），赛视智能（Saige Research），三星研究院

关键词：时间序列数据插补，概率模型，不确定性

参考文献：Kim S H, Kim H, Yun E, et al. Probabilistic imputation for time-series classification with missing data[C]//International Conference on Machine Learning. PMLR, 2023: 16654-16667.

摘要

实际应用的多变量时间序列数据通常包含大量缺失值。对此类缺失值进行分类的主要方法是使用特定值（零、平均值、相邻时间步长的值）或可学习参数进行启发式插补。然而，这些简单的策略没有考虑到数据生成过程，更重要的是，由于缺失值的多种可能性，无法有效地捕捉预测中的不确定性。在本文中，提出了一种新的概率框架，用于对缺失值的多变量时间序列数据进行分类。模型由两部分组成：用于缺失值插补的深度生成模型和分类器。

Method

提出的方法在MNAR假设下将supMIWAE扩展到时间序列数据。

设可观察值 $x_{1,T}^o$ ，缺失值 $x_{1,T}^m$ ，缺失值的掩码 $s_{1,T}$ ，标签 $y$，潜在空间向量 $z_{1:T}$ 。

Prior

假设Gaussian过程先验对 $z_{1:T}$ 潜在空间中的时间相关性进行编码，可得先验$p_{\theta }(z_{1:T})$：

$$p_{\theta }(z_{1:T})=\prod _{j=1}^{d}N(z_{1:T,j}|0,K)$$

K i j = k ( t i , t j ) i , j ∈ { 1 … T } K _ { i j } = k ( t _ { i } , t _ { j } ) \quad i , j \in \left\{ 1 \ldots T \right\} Kij​=k(ti​,tj​)i,j∈{1…T}

其中，$k(.,.)$ 是核函数，在本文的所有实验中都使用 Cauchy 核。

Decoder

对观察到的 $p_{\theta }(x_{1:T}^o|z_{1:T})$ 的解码器以自回归方式定义：

$$p_{\theta }(x_{1,T}^o|z_{1,T})=\prod _{t=1}^{T}N(x_t^o|{\mu }_{dec}(z_{1,t}),diag({\sigma }_{dec}^2(z_{1,t})))$$

其中$ (\mu _ { d e c } ( z _ { 1 , t } ) , \sigma _ { d e c }( z _ { 1 , t } ))_{t=1}^{T} $用具有因果掩码的transformer定义。

$$h_t=Transforme{r}_{dec}(z_{1:t})$$

$$({\mu }_{dec}(z_{1:t}),{\sigma }_{dec}(z_{1:t}))=ML{P}_{dec}(h_t)$$

对观测$p_{\theta }(x_{1:T}^o|z_{1:T})$和缺失$p_{\theta }(x_{1:T}^m|z_{1:T})$都使用相同的Decoder。

Missing model

缺失模型$p_{\psi }(s_{1:T}|x_{1:T})$被假设为随时间步长和特征的独立伯努利分布:

$$p_{\psi }(s_{1:T}|x_{1:T})=\prod _{t=1}^T\prod _{j=1}^{d}Bern(s_{t,j}|{\sigma }_{mis,t,j}(x_{1:T}))$$

$${\sigma }_{mis}(x_{1:T})=ML{P}_{mis}(x_{1:T})$$

Classifier

使用基于 transformer 的模型构建分类器：给定一个时间序列数据 $x_{1:T}$ 将观测值 $x_{1:T}^o$ 和从解码器生成的插补缺失值打包在一起，首先使用沿时间轴的一维 CNN 处理数据以计算 $r_{1:T}=CNN(x_{1:T})$ 。 然后用transformer模块处理 $r_{1:T}$ 来计算输出 $h_T$。条件分布 $p_{\lambda }(y|x_{1:T}^o,x_{1:T}^m)$ 定义为

$$Categorical(y|Softmax(Linea{r}_{cls}(h_T))$$

在前向传递过程中，分类器获取观察到的输入 $x_{1:T}^o$ 和从解码器 $p_{\theta }(x_{1:T}^m|z_{1:T})$生成的缺失值。 实验发现采用 GRU-D 是有益的，而不是直接使用生成的缺失值 $x_{1:T}^m$ ，将衰减的缺失值计算如下：

$${\tilde{x}}_{1:T}:=(x_{1:T}^o,x_{1:T}^m)where{x}_{1:T}^m\sim p_{\theta }(x_{1:T}^m|z_{1:T})$$

$${\hat{x}}_{t,j}=Decay(s_{t,j},x_{t,j},{\gamma }_{{\hat{x}}_{t,j}},x_{t^{\prime },j},{\tilde{x}}_{t,j})$$

其中，${\gamma }_{{\hat{x}}_t}=exp(-max(0,W_{\hat{x}}{\delta }_t+b_{\hat{x}})$ 是可学习的衰减。

Encoder

给定上面定义的生成模型，引入了 ( x _ { 1 : T } ^ { m } , z _ { 1 : T } ) 的变分分布，其分解为：

$$p_{\theta }(x_{1:T}^m|z_{1:T})q_{\varphi }(z_{1:T}|x_{1:T}^o)$$

这里，编码器 $q_{\varphi }(z_{1,T}|x_{1:T}^o)$ 被定义为一个自回归模型，如前所述，

$$q_{\varphi }(z_{1,T}|x_{1:T}^o)=\prod _{t=1}^{T}N(z_t|{\mu }_{enc}(x_{1,t}^o),diag({\sigma }_{enc}^2(x_{1,t}^o)))$$

给定一系列观测值 $x_{1:T}^o$，首先对缺失值应用零插补，即，如果 $s_{t,j}=1$ 并且 $x_{t,j}^{\prime }=0$ ，则 $x_{t,j}^{\prime }=x_{1:T}^o$。然后，将missing indicators拼接到 $x_{1,T}^{\prime }$ ，并将1D CNN应用于时间轴，如$r_{1:T}=CNN(x_{1,T}^{\prime })$。在计算了 $r_{1:T}$ 之后，与解码器类似，使用具有因果掩码的transformer来计算:

$$h_t=Transforme{r}_{dec}(r_{1:t})$$

$$({\mu }_{dec}(x_{1:t}^o),{\sigma }_{dec}(x_{1:t}^o))=ML{P}_{dec}(h_t)$$

Objective

定义了所有组成后，supernotMIWAE的IWAE界限计算如下：

$$L^{(K)}(\lambda ,\theta ,\psi ,\varphi ):=E\left[\log \frac{1}{K}\sum _{k=1}^K{\omega }_k\right]$$

$${\omega }_k:=p_{\lambda }(y|x_{1:T}^o,x_{k,1:T}^m)p_{\psi }(s_{1:T}|x_{1:T}^0,x_{k,1:T}^m)\times p_{\theta }(x_{1:T}^o|z_{k,1:T})p_{\theta }(z_{k,1:T})/q_{\varphi }(z_{k,1:T}|x_{1:T}^o)$$

其中，${\omega }_k$ 是重要性权重项。

ObsDropout

ObsDropout 用来正则化 supnotMIWAE 以获得更好的插补效果。因为前述目标函数缺乏明确的监督目标，使用该目标训练的模型不太可能生成实际的缺失值。

ObsDropout：当将观测到的输入 $x^{o}_{1:T} $和插补缺失值 $x_{1:T}^m$ 传递给分类器时，故意删除观测到的输入的某些部分。在不丢弃观测到的输入的情况下，分类器可能严重依赖观测到的输入来进行分类，但如果在训练过程中丢弃了一些观测到的输入，分类器可以更多地关注插补缺失值 $x_{1:T}^m$。因此，鼓励模型生成更多有利于分类的“有用”缺失值。更具体地说，让$\beta$是一个预定义的Dropout概率。然后，将插补的输入 $\hat{x}$ 构造到分类器，如下所示：

$${\hat{x}}_{1:T}:=(x_{1:T}^o,x_{1:T}^m)where{x}_{1:T}^m\sim p_{\theta }(x_{1:T}^m|z_{1,T})$$

$$m_{t,j}=Bern(1-\beta )$$

$${\hat{x}}_{t,j}=Decay(s_{t,j},x_{t,j},{\gamma }_{{\hat{x}}_{t,j}},x_{t^{\prime },j},{\tilde{x}}_{t,j})$$

Prediction

与 SupMIWAE 类似，利用自归一化重要性抽样 （SNIS） 来近似新输入 $x_{1:T}^o$ 的预测分布。

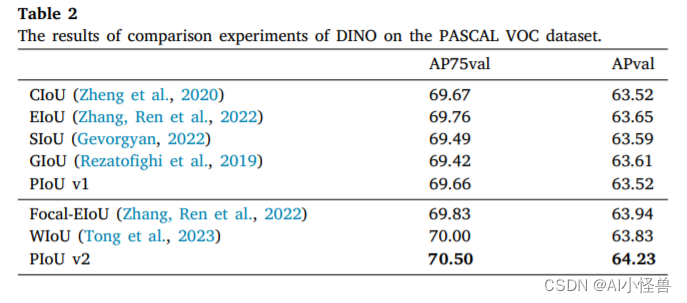
实验结果