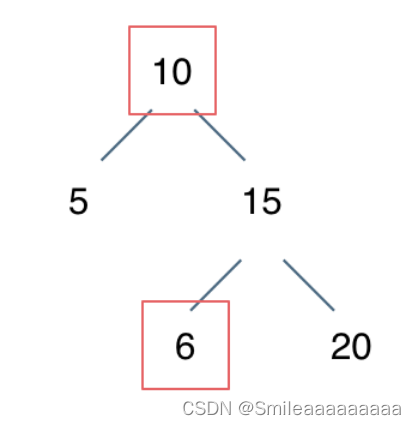
💡💡💡本文改进内容: CVPR2023 SCConv 由两个单元组成:空间重建单元(SRU)和通道重建单元(CRU)。 SRU利用分离重建方法来抑制空间冗余,而CRU使用分割-变换-融合策略来减少通道冗余。
改进结构图如下:
YOLOv9魔术师专栏
☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️ ☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️
包含注意力机制魔改、卷积魔改、检测头创新、损失&IOU优化、block优化&多层特征融合、 轻量级网络设计、24年最新顶会改进思路、原创自研paper级创新等
☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️☁️
✨✨✨ 新开专栏暂定免费限时开放,后续每月调价一次✨✨✨
🚀🚀🚀 本项目持续更新 | 更新完结保底≥80+ ,冲刺100+ 🚀🚀🚀
🍉🍉🍉 联系WX: AI_CV_0624 欢迎交流!🍉🍉🍉
⭐⭐⭐现更新的所有改进点抢先使用私信我,目前售价68,改进点20+个⭐⭐⭐
⭐⭐⭐专栏涨价趋势 99 ->199->259->299,越早订阅越划算⭐⭐⭐

YOLOv9魔改:注意力机制、检测头、blcok魔改、自研原创等
YOLOv9魔术师
💡💡💡全网独家首发创新(原创),适合paper !!!
💡💡💡 2024年计算机视觉顶会创新点适用于Yolov5、Yolov7、Yolov8等各个Yolo系列,专栏文章提供每一步步骤和源码,轻松带你上手魔改网络 !!!
💡💡💡重点:通过本专栏的阅读,后续你也可以设计魔改网络,在网络不同位置(Backbone、head、detect、loss等)进行魔改,实现创新!!!
1.YOLOv9原理介绍

论文: 2402.13616.pdf (arxiv.org)
代码:GitHub - WongKinYiu/yolov9: Implementation of paper - YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information摘要: 如今的深度学习方法重点关注如何设计最合适的目标函数,从而使得模型的预测结果能够最接近真实情况。同时,必须设计一个适当的架构,可以帮助获取足够的信息进行预测。然而,现有方法忽略了一个事实,即当输入数据经过逐层特征提取和空间变换时,大量信息将会丢失。因此,YOLOv9 深入研究了数据通过深度网络传输时数据丢失的重要问题,即信息瓶颈和可逆函数。作者提出了可编程梯度信息(programmable gradient information,PGI)的概念,来应对深度网络实现多个目标所需要的各种变化。PGI 可以为目标任务计算目标函数提供完整的输入信息,从而获得可靠的梯度信息来更新网络权值。此外,研究者基于梯度路径规划设计了一种新的轻量级网络架构,即通用高效层聚合网络(Generalized Efficient Layer Aggregation Network,GELAN)。该架构证实了 PGI 可以在轻量级模型上取得优异的结果。研究者在基于 MS COCO 数据集的目标检测任务上验证所提出的 GELAN 和 PGI。结果表明,与其他 SOTA 方法相比,GELAN 仅使用传统卷积算子即可实现更好的参数利用率。对于 PGI 而言,它的适用性很强,可用于从轻型到大型的各种模型。我们可以用它来获取完整的信息,从而使从头开始训练的模型能够比使用大型数据集预训练的 SOTA 模型获得更好的结果。对比结果如图1所示。

YOLOv9框架图
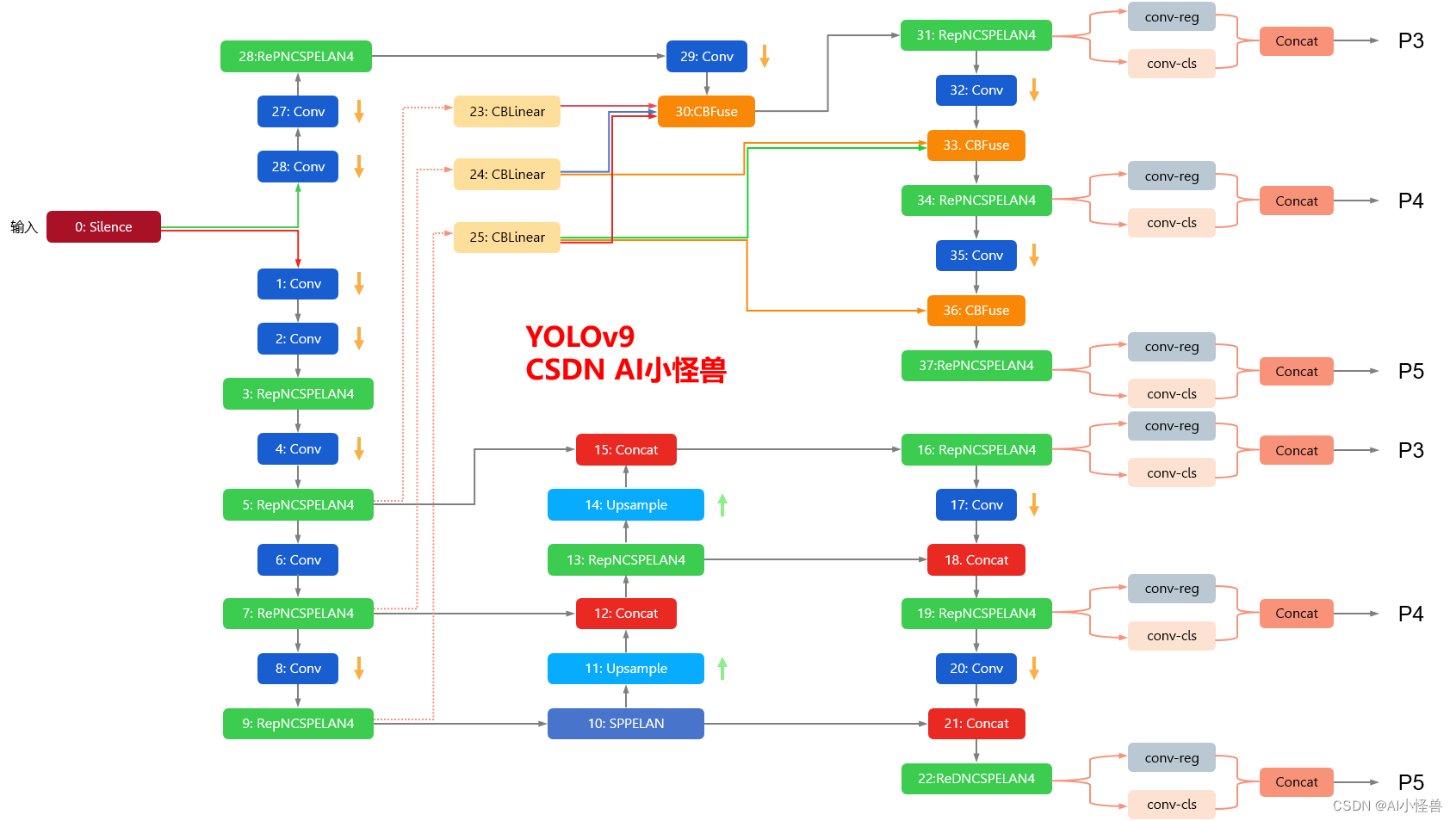
1.1 YOLOv9框架介绍
YOLOv9各个模型介绍

2. SCConv介绍

论文:https://openaccess.thecvf.com/content/CVPR2023/papers/Li_SCConv_Spatial_and_Channel_Reconstruction_Convolution_for_Feature_Redundancy_CVPR_2023_paper.pdf
卷积神经网络(CNN)已经实现在各种计算机视觉任务中表现出色,但这是以巨大的计算成本为代价的资源,部分原因是卷积层提取冗余特征。 在本文中,我们尝试利用特征之间的空间和通道冗余,针对 CNN 压缩,提出了一种高效的卷积模块,称为 SCConv(空间和通道重建卷积),以减少冗余计算,并促进代表性特征学习。 提出的 SCConv 由两个单元组成:空间重建单元(SRU)和通道重建单元(CRU)。 SRU利用分离重建方法来抑制空间冗余,而CRU使用分割-变换-融合策略来减少通道冗余。 此外,SCConv 是一个即插即用的架构单元,可以可以直接用来替代各种卷积神经网络中的标准卷积。 实验结果表明SCConv 嵌入式模型能够实现更好的效果
通过减少冗余特征来显着降低复杂性和计算成本来提高性能。
SCConv 的结构包括了空间重建单元(SRU)和通道重建单元(CRU)。 下图显示了我们的 SCConv 模块添加在 ResBlock 中的确切位置 。
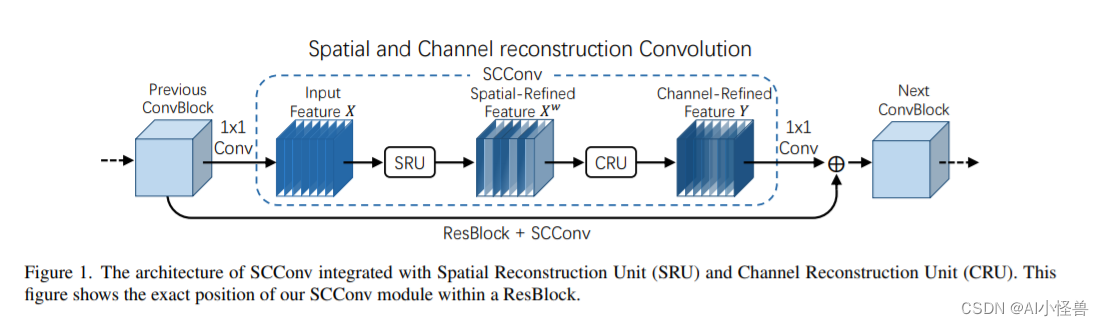
SRU结构:

CRU结构:
 实验结检测:
实验结检测:

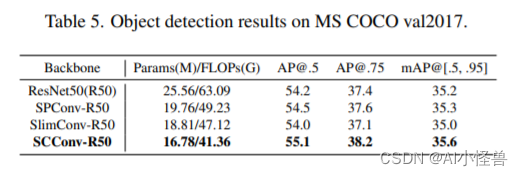
3.SCConv加入到YOLOv9
3.1新建py文件,路径为models/Conv/SCConv.py
本部分转为付费专栏开放
3.2修改yolo.py
1)首先进行引用
from models.Conv.SCConv import SCConv2)修改def parse_model(d, ch): # model_dict, input_channels(3)
在源码基础上加入SCConv
n = n_ = max(round(n * gd), 1) if n > 1 else n # depth gain
if m in {
Conv, AConv, ConvTranspose,
Bottleneck, SPP, SPPF, DWConv, BottleneckCSP, nn.ConvTranspose2d, DWConvTranspose2d, SPPCSPC, ADown,
RepNCSPELAN4, SPPELAN,SCConv}:
c1, c2 = ch[f], args[0]
if c2 != no: # if not output
c2 = make_divisible(c2 * gw, 8)
args = [c1, c2, *args[1:]]3.3 yolov9-c-SCConv.yaml
实验中,待更新
⭐⭐⭐现更新的所有改进点抢先使用私信我,目前售价68,改进点20+个⭐⭐⭐
⭐⭐⭐专栏涨价趋势 99 ->199->259->299,越早订阅越划算⭐⭐⭐