学习周报：文献阅读+Fluent案例+水力学理论学习

摘要

Abstract

文献阅读：

文献摘要

现有问题

研究目的及方法

PINN的设置

NS方程介绍

损失函数

训练方法

实验设置

对照组设置

实验结果展示

点云数、隐藏层数和每个隐藏层的节点数对PINN精度的影响

点云数对PINN的影响：

隐藏层数的影响

每个隐藏层的节点数的影响

结果讨论

PINN与CFD所消耗资源对比

结论

Fluent 案例：催化转换器模型的内流场仿真

几何建模部分

网格划分部分

求解器部分

理论学习部分

总结

摘要

在本周中，通过阅读文献，对PINN在流体力学中的研究进行了解，在本次总结中选取其中一篇，低雷诺数情况下，PINN对圆柱绕流的预测和CFD的对比进行描述。Fluent中，选用催化转换器模型的内流场仿真，了解多孔介质流动在fluent中如何实现。理论学习方面，对层流和紊流相关知识进行了学习。

Abstract

In this week, I read the literature to understand the research of PIN in fluid mechanics, and in this summary,and chose one of the articles to describe the prediction of cylindrical flow and CFD in the case of low Reynolds number. In Fluent, the internal flow field simulation of the catalytic converter model was used to understand how the flow of porous media is implemented in Fluent. In terms of theoretical learning, the knowledge related to laminar flow and turbulence flow was studied.

文献阅读：

Physics-Informed Neural Networks for Low Reynolds Number Flows over Cylinder

低雷诺数圆柱流动的物理信息神经网络（PINN）

文献摘要

PINN可以用于流体动力学的代替模型，以降低计算成本，本次阅读的文献以使用PINN来验证流体力学中的公式，并以经典的低雷诺数圆柱绕流的案例呈现。在PINN架构中，层数的增加对结果精度的提高最大，其次是点云中点数的增加。增加每个隐藏层的节点数量带来的性能提升最小；且所需的计算内存比CFD更少，但所需的时间更长。文中也演示了不需要数据的PINN的直接公式，以及超参数设计和计算需求的比较。

现有问题

CFD的预处理步骤需要生成计算网格，特别是对于具有运动边界的复杂区域，网格生成不好可能导致结果不准确。
所需时间过长，尽管最近计算能力有所提高，但使用CFD进行流体模拟仍然对计算量要求很高，特别是对于必须执行多次迭代的设计过程。
若使用其余替代模型，例如CNN、LTSM等，所需的训练数据庞大，使用CFD或实验数据训练网络也限制了模型在非常具体问题上的应用。

研究目的及方法

目的：

证明使用PINN来解决低雷诺数流动，并研究影响PINN架构设计的关键因素；包括改变神经网络层、节点的数量和点云的大小。

方法：

将把NavierStokes方程纳入到训练过程中，在不使用任何模拟或实验数据的情况下预测圆柱体的流场，为计算域的边界规定了自由流条件，并将用于训练PINN。

PINN的设置

NS方程介绍

在不可压缩流体中，NS方程表示为：

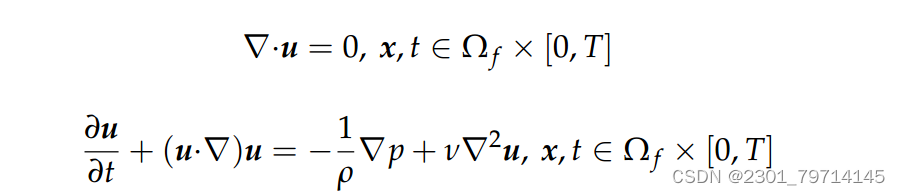
（其中t、x分别为时间坐标和空间坐标，u为速度矢量，p为压力，r、n分别为流体密度和运动粘度，Wf∧R3表示流体域）

初始和边界条件表示如下：

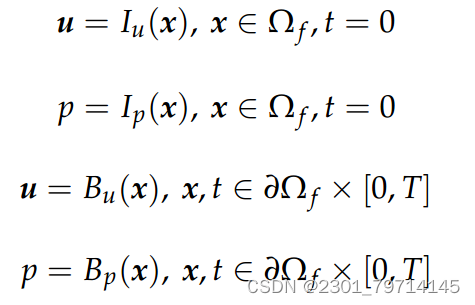
（Wf表示计算域的边界。控制方程、初始条件和边界条件必须在区域内完全满足）

若方程中出现不平衡的情况，即表明流场计算中存在误差，故需将不可压缩流体的NS方程积分后，加入PINN的损失函数中。

损失函数

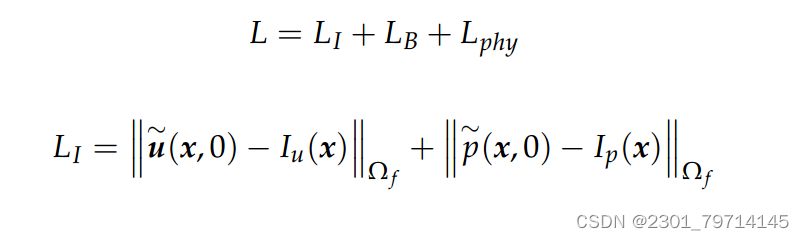
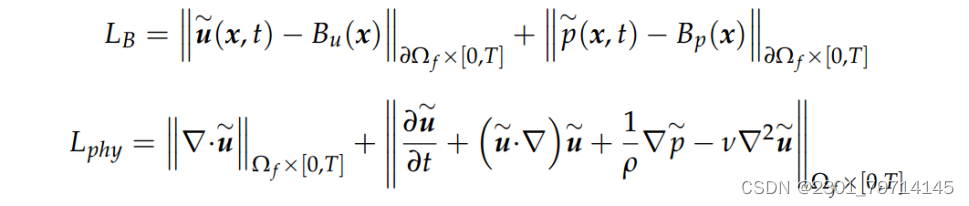
如上式所示，损失函数中包括速度和压力的预测值，LI表示在初始条件下的损失情况，LB为边界处的损失函数，它们由PINN预测值与规定值之差的大小给出。Lphy表示物理中的损失，其中第一项和第二项分别是Navier-Stokes方程的连续性方程和动量方程的误差。为了满足Navier-Stokes方程，必须消除两个方程的误差。因此，任何非零误差值都可以视为对PINN的损失。Navier-Stokes方程的空间导数是使用自动微分计算的。在这种情况下，自动微分比数值微分更可取，因为后者会因选择有限差分格式而导致截断误差，而自动微分则提供基于PINN作为连续函数的解析导数。由于PINN的目标是通过最小化流体域的误差来求解控制方程，因此训练和求解步骤不需要实验或模拟数据。

训练过程以迭代或epoch的方式进行，从输入特征的前向传播开始，以计算每个点的速度和压力的预测输出值。输出值用于计算Navier-Stokes方程所需的空间导数。导数是使用自动微分计算，利用这些导数，计算自定义物理的损失函数。在每个历元中，优化器旨在减小损失函数，从而减小Navier-Stokes方程的残差和误差，以解决给定边界条件下的流动问题。

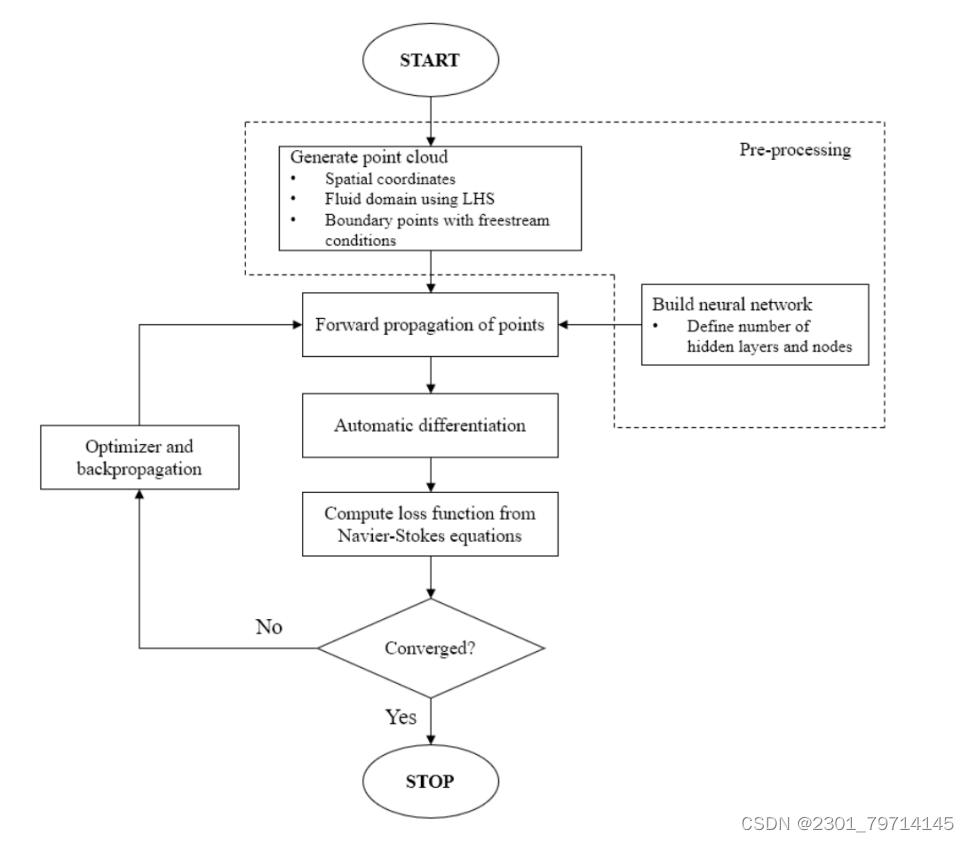
使用点云作为输入数据的流场预测PINN框架如下图：

训练方法

使用PyTorch建立一个完全连接的神经网络。在神经网络的建立中定义了隐藏层数、节点数和激活函数。其次，采用拉丁超立方体采样(LHS)生成流体域和边界的点云。

如下图所示，该案例为在二维稳定情况下，流体域点云中的每个点都包含x和y坐标，它们作为全连接网络训练的输入特征。输入特征的前向传播开始，以计算每个点的速度和压力的预测输出值。输出值用于计算Navier-Stokes方程所需的空间导数。

再利用PINN自动微分的特性，来计算速度和压力的导数，并用与计算所定义的损失函数，减少NS方程中的残差及误差。

实验设置

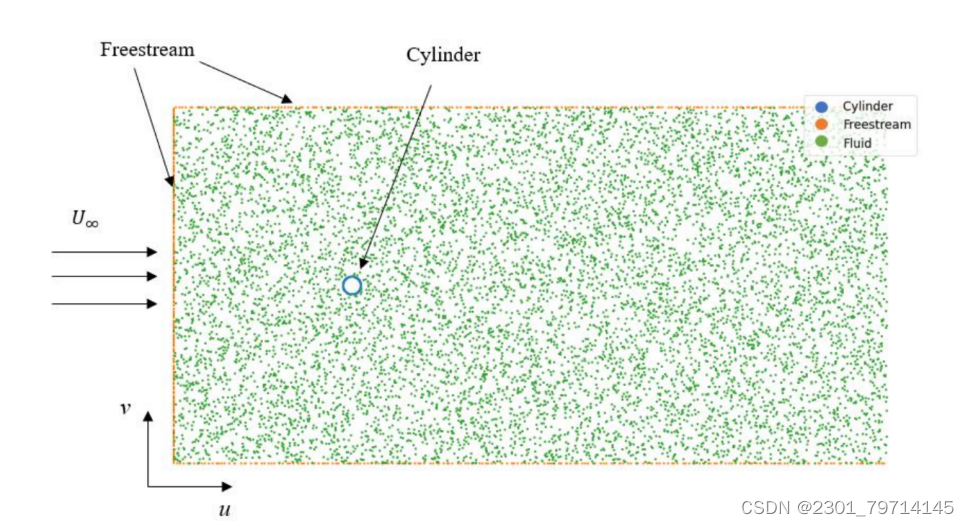
本文中使用低雷诺数的圆柱绕流来演示PINN，并研究点密度、层数和节点对其精度的影响。其点云包括自由流边界、圆柱体边界以及流体域中用于计算Navier-Stokes方程中的误差和不平衡的配点,点云的坐标是使用LHS随机生成的。

由于PINN不是使用几个相邻的点来计算导数，而是使用自动微分来在每个单点上执行控制方程，故采用LHS在整个流体域中产生随机但均匀的点云，而不是在圆柱体周围产生更大密度的点云。可以获得更准确的效果。

文献中设置中，沿柱面放置180个点，在自由流边界条件下放置600个点。由于本案例用于研究PINN中各种关键因素的影响，因此点、层和节点的数量根据表1而变化，并且使用3000个epoch以达到低于10−3的均方根误差(RMSE)（随着epoch数的增加，损失并没有进一步减少），所布置点云示意图如下所示：

（圆柱流动参数化研究的参数）

对照组设置

对圆柱绕动进行了CFD模拟，将缸体上的流动作为一个简单的测试用例，对PINN进行参数化研究，并评估PINN模拟钝体上流动的能力。用有限体积法求解了稳态不可压缩的Navier-Stokes方程。对于二维不可压缩稳态问题，控制方程化为:

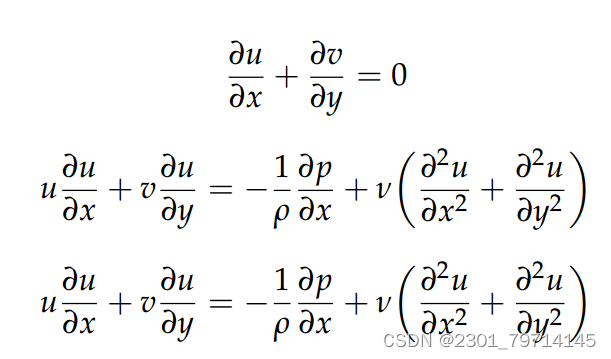
使用CFD定义了一个40 D × 20 D的计算域，其中D = 0.1 m为圆柱体直径。虚线箭头从圆柱体的上表面延伸到计算域的上边缘，表示将绘制各种流场的线，以比较CFD和PINN的结果。

网格由六面体单元组成，并对近壁单元的厚度进行了细化，以保证边界层的清晰定义。入口速度为1m /s，运动粘度n = 2 × 10−2 m2/s，从圆柱体中心向上游10 D处，计算域的上下边界处。在这种情况下得到的雷诺数是5。选择低雷诺数以保证流动稳定，不发生旋涡脱落。该区域的右边界指定为压力出口，其位置为距圆柱体中心30d处。在圆柱体表面施加无滑移边界条件。

网格划分情况与计算示意图如下：

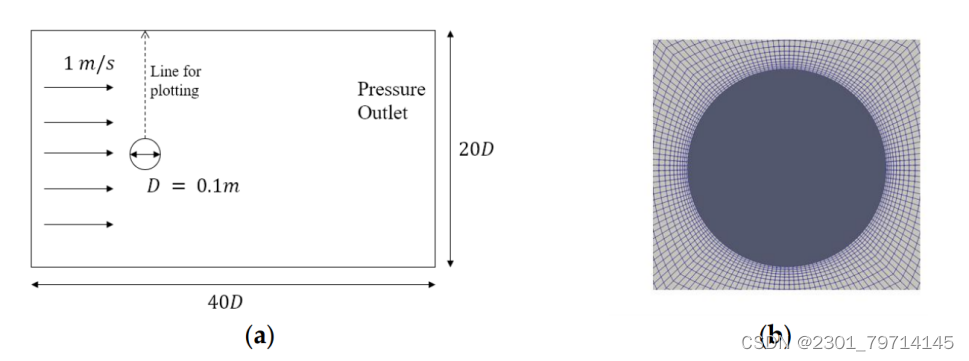
采用压力链接方程半隐式方法(SIMPLE)算法迭代更新速度和压力，空间离散化采用二阶迎风格式。

实验结果展示

点云数、隐藏层数和每个隐藏层的节点数对PINN精度的影响

点云必须有足够的密度来分辨圆柱附近的流场。点云中点的不足会导致边界层的解析不佳，从而导致整个域的结果不理想。隐藏层数和每个隐藏层的节点数共同影响PINN的表达能力。

如果隐藏层数量不足，PINN将需要大量节点才能获得准确的结果，从而导致训练过程中的计算开销很高。节点数量不足将不得不通过大量隐藏层来弥补。

（下表显示了本参数化研究中使用的点数、隐藏层数和每个隐藏层的节点数）

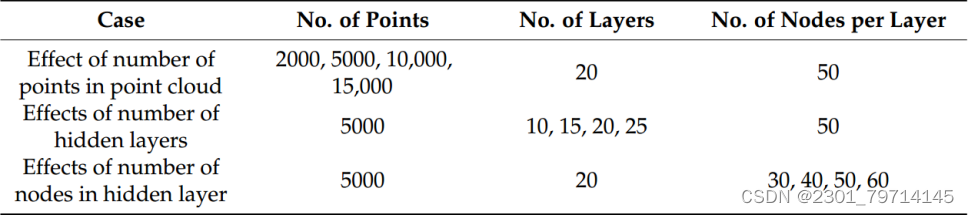
点云数对PINN的影响：

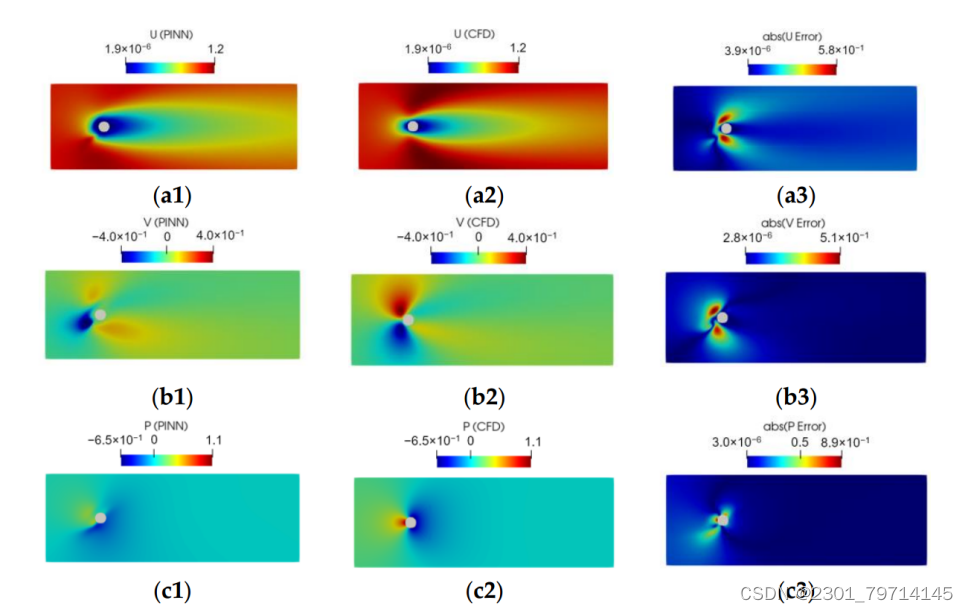
上图为来自PINN和CFD的点云中2000个点的u速度分量、v速度分量和压力场。并显示出误差。当在流体域中仅使用2000个点时，PINN无法获得与CFD相当的结果。PINN无法捕获正确的前缘速度分布，以及正确的压力场和大小。这表明，在这种情况下，创建流体域的2000个点过于稀疏，无法准确捕获正确的速度和压力场。

从2000点增加到5000点，PINN开始以更高的精度捕获速度和压力场。虽然PINN和CFD的速度分布相似，但PINN捕获的速度幅度更小，流动加速面积更小。可见下图:

在将点的数量从5000增加到10,000之后，速度分量没有任何改善。u型速度分量捕获了尾迹剖面，但前缘周围的速度幅值和加速流动区域的速度幅值减小了。同样，对于v型速度剖面，趋势被很好地捕捉到，但速度较大的区域也被削弱了。然而，当观察压力剖面时，由PINN捕获的剖面开始看起来更加对称。与之前一样，PINN捕获的压力值小于CFD捕获的压力值。

从10,000增加到15,000，并没有提高PINN的速度和压力剖面的精度，故不在详细叙述，点云数量对PINN的预测影响总体可见下图：

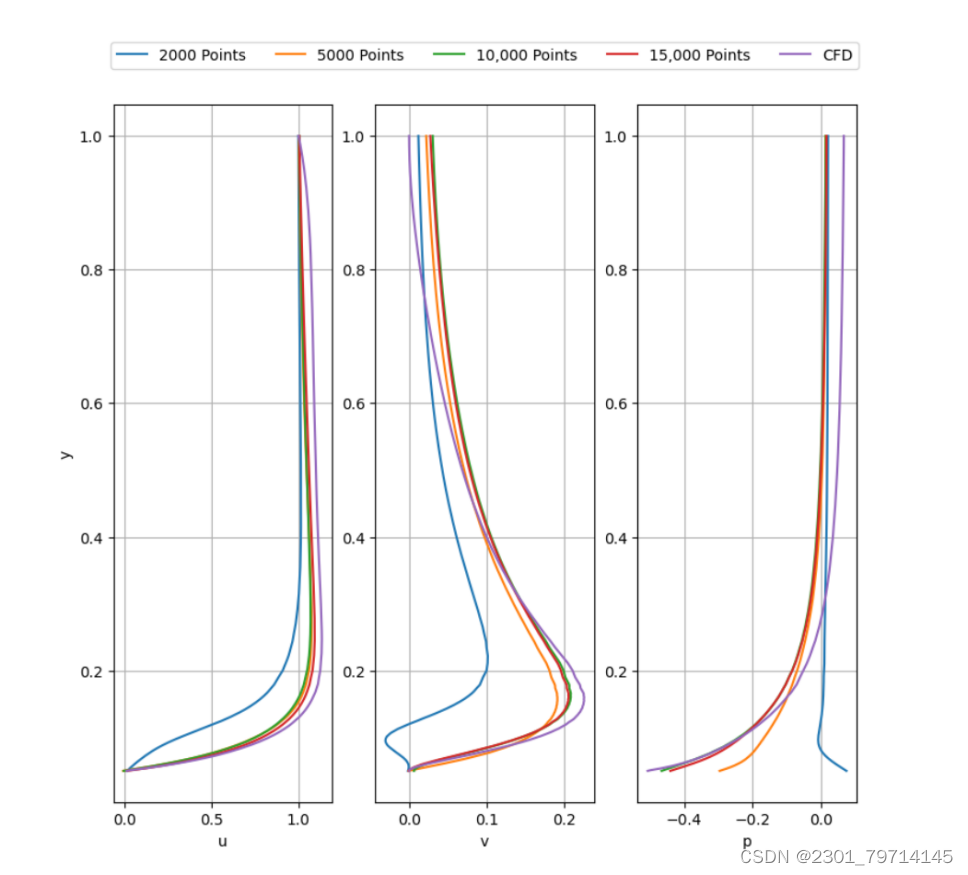
（不同个数点从柱体顶面到计算域边缘的u速度、v速度和压力场线形图）

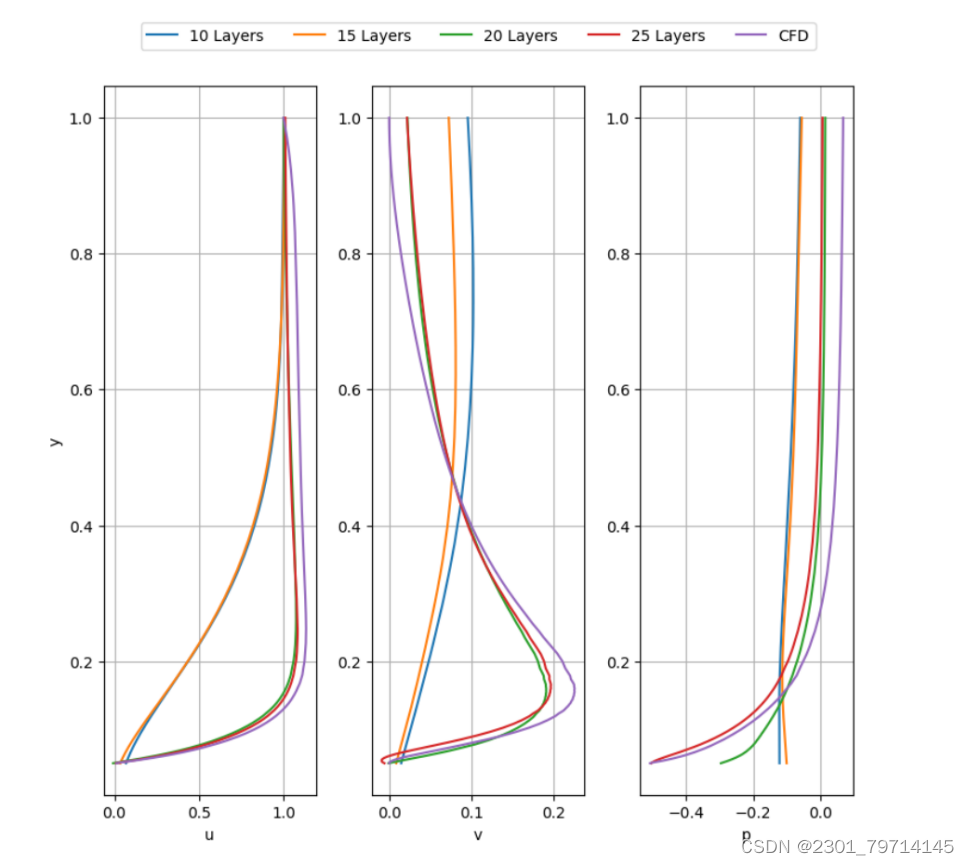
隐藏层数的影响

隐藏层本质上是创建复合函数。通过拥有更多的隐藏层，PINN能够捕获更复杂的问题，例如那些具有大梯度或不连续的问题。如果隐藏层的数量不足，将导致简单、平滑的解决方案，这可能会损害准确性。为了研究效果，点云中的点数和每层的节点数分别保持在5000个点和50个节点。然后研究了10、15、20和25个隐藏层的PINN精度。

对于10个隐藏层，圆柱体周围的u速度流场如下图所示，其中PINN无法产生准确的结果。15个隐藏层的结果与10个隐藏层的结果相似，其中PINN无法准确捕获圆柱体周围的速度和压力场。

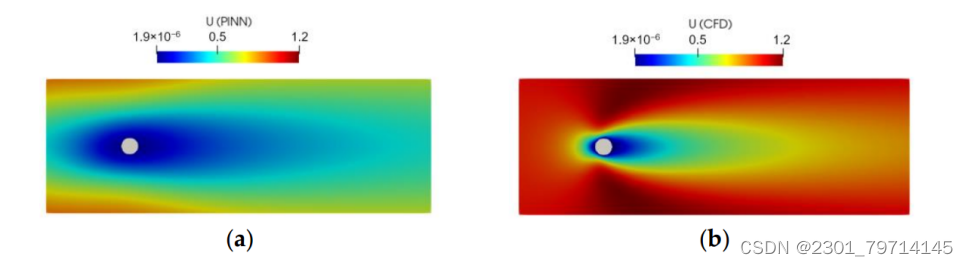
其余20、25层数的隐藏层结果详情可见文献，实验过程相似，故不再过多赘述，具体误差可见下图：

每个隐藏层的节点数的影响

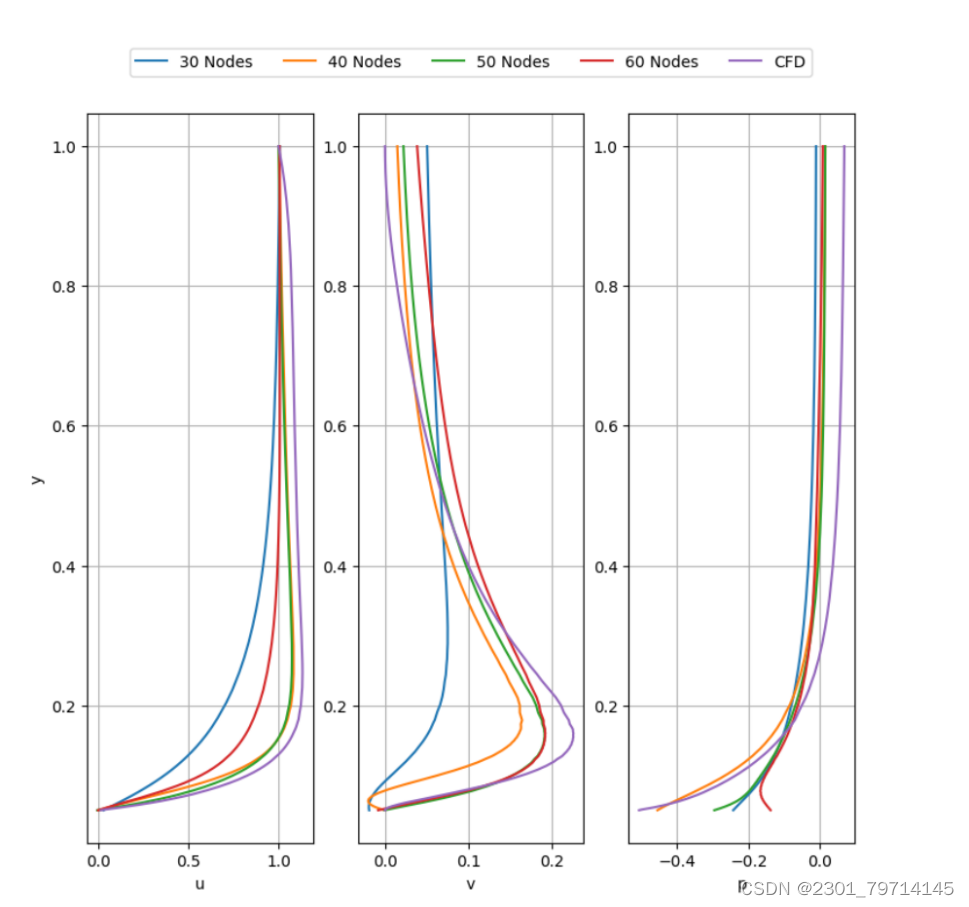
使用5000个点云的PINN对30、40、50个隐藏层节点数进行对比，实验过程同上，仅利用30个节点的神经网络无法准确预测u速度分量、v速度分量和压力的流场。当每个隐藏层的节点数从30个增加到40个时，可以看到精度的显著提高。然而，PINN和CFD的结果之间仍然存在一些差异。

对于50个节点，PINN产生的结果的准确性有一定的提高。除了PINN捕获的流动加速区域周围的速度值较低外，尾迹和前缘u速度分量的一致性较好。同样，与CFD结果相比，PINN计算的v速度分量也遵循类似的趋势。PINN计算的压力场与CFD计算结果吻合较好。除了滞止压力低于CFD结果外，气缸上风向的高压区域和气缸下风向的低压区域都得到了很好的捕捉。

用60个节点时，PINN计算的u速度分量尾迹区域比CFD计算的尾迹区域长。与CFD计算结果相比，PINN计算的前缘区域也出现了锥形扩展。PINN也不能很好地捕获流加速区域。故有结论：一般来说，从50个节点增加到60个节点并不能提高PINN的准确性。

下图绘制了CFD和PINN在每个隐藏层节点数不同时的u和v速度分量和压力。对于u速度分量，使用30个节点的PINN与CFD计算结果存在较大偏差。40节点和50节点的PINN表现更好，结果与CFD非常接近。然而，将节点数量增加到60会导致性能下降，这与图12中观察到的流场一致。具有50和60个节点的PINN能够以较高的精度捕获近场v速度，但与前面的情况类似，在fa中可以观察到轻微的偏差：

结果讨论

一般情况下，PINN计算出的震级要小于CFD计算结果。这种微小的差异可能是由于压力计算的困难造成的。压力在动量方程中没有明确的定义，只是由连续性方程间接地施加。

本文献中提出了将压力泊松方程，并将其作为损失的一部分纳入神经网络的猜想，但结果有待研究。

对于不同数量的点、隐藏层和每个隐藏层的节点，对于u和v速度分量，PINN和CFD之间的最大绝对误差如图所示，从点数的结果来看，在点云中达到5000点后，精度停滞不前。

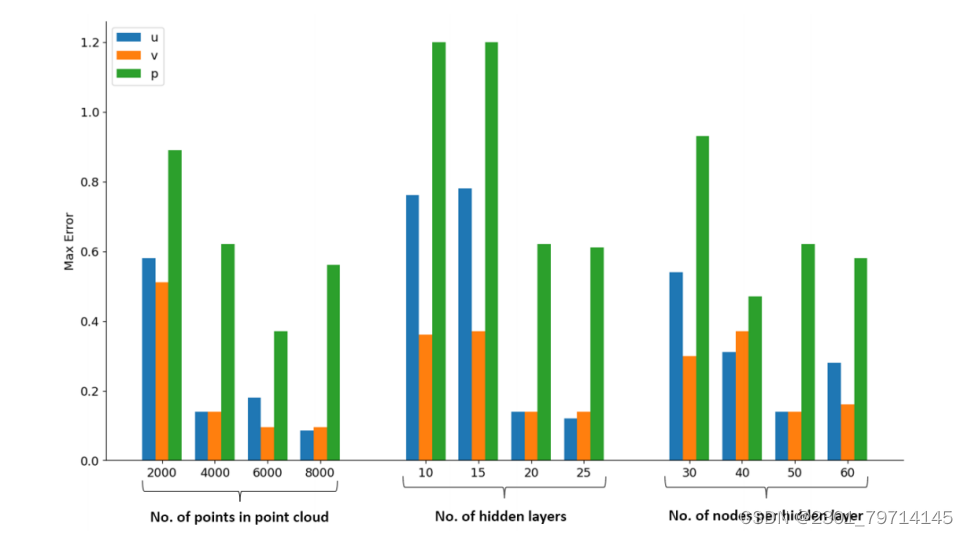
表明，一旦使用了所需的最小点数，点数的增加并不会导致更精确的速度场。对于图中的压力场误差，10,000点的情况下获得的最大绝对误差最小，因为压力在Navier-Stokes方程中是隐式定义的，所以很难训练压力场，增加点的数量会导致误差放大。

当隐藏层数从20层增加到25层时，最大误差并没有明显降低，但PINN产生的尾迹精度明显降低。对于使用25个隐藏层的网络，PINN无法获得精确的尾迹速度大小。这可能主要是由于当网络规模变大时，训练难度增加，导致准确率降低，这些情况下的准确性达到了20个隐藏层的极限，任何额外的层都不会进一步改善结果。

对于网络中每个隐藏层的节点数不同，节点数不足导致PINN无法在整个空间尺度上完全泛化解。当每个隐藏层的节点数从50增加到60时，PINN结果的准确性会降低。增加每个隐藏层的节点数量增加了训练参数的维度，这使得训练PINN更加困难，导致精度降低。

从研究中可以看出，增加每个隐藏层的节点数量对PINN的性能改善最小。

PINN与CFD所消耗资源对比

PINN和CFD的计算资源使用情况与点云中点数的比较如图所示：

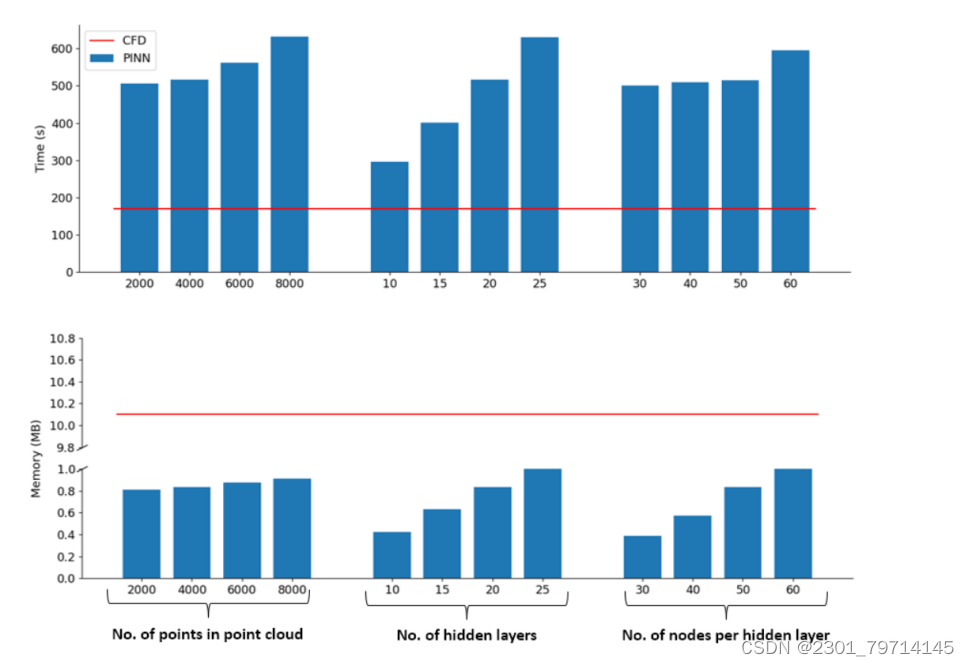
PINN的时间复杂度与层数呈线性关系。将PINN算法与CFD算法的求解时间进行比较，发现PINN算法求解含20个隐藏层的圆柱绕流所需的时间几乎是CFD算法的3倍。在计算时间方面，CFD仍然更加高效，自动微分过程是造成计算时间长的主要原因。然而，当涉及到内存使用时，PINN能够弥补这一点。随着隐藏层数量的增加，PINN内存使用量呈线性变化。

在内存使用方面，PINN的效率是CFD的5倍以上，因此解决问题u时对硬件的要求较低。

然而，PINN在时间效率上的不足，在空间效率上得到了弥补。在所有情况下，与CFD相比，PINN需要的内存大约少10倍。PINN的数据格式为简单张量，仅包含神经网络的空间坐标、权值和偏置。与PINN不同，定义CFD网格的数据更复杂，包括单元顶点、单元面和单元邻域，这导致CFD占用更大的内存。

（CFD与PINN计算时间的比较）

结论

从该案例中可看出，证明了流体流动的物理信息神经网络(PINN)架构适用于低雷诺数的圆柱体周围流动。PINN能够捕捉到流场的总趋势。PINN产生的速度场与CFD获得的结果具有可比性。然而，由于压力项在损失函数中没有明确定义，PINN在压力场预测中出现困难。

且对于各个影响因素，可以看出：增加层数对结果精度的提高最大，其次是增加点云中的点数。增加每个隐藏层的节点数量带来的性能提升最小。

在计算需求方面，PINN在内存使用方面比CFD更有效，但在计算时间方面不是必需的。在CFD网格中单元数较低的简单情况下，PINN比CFD计算结果所需的时间更长。然而，在更复杂的情况下，在CFD网格中涉及到更多的单元，PINN有可能更节省时间。

Fluent 案例：催化转换器模型的内流场仿真

几何建模部分

该案例中存在多孔介质，为各向异性的多孔介质，在建模时，需画出其固体区域及多孔介质，而流体域部分可以通过fluent meshing水密工作流来进行抽取。模型如下图所示：

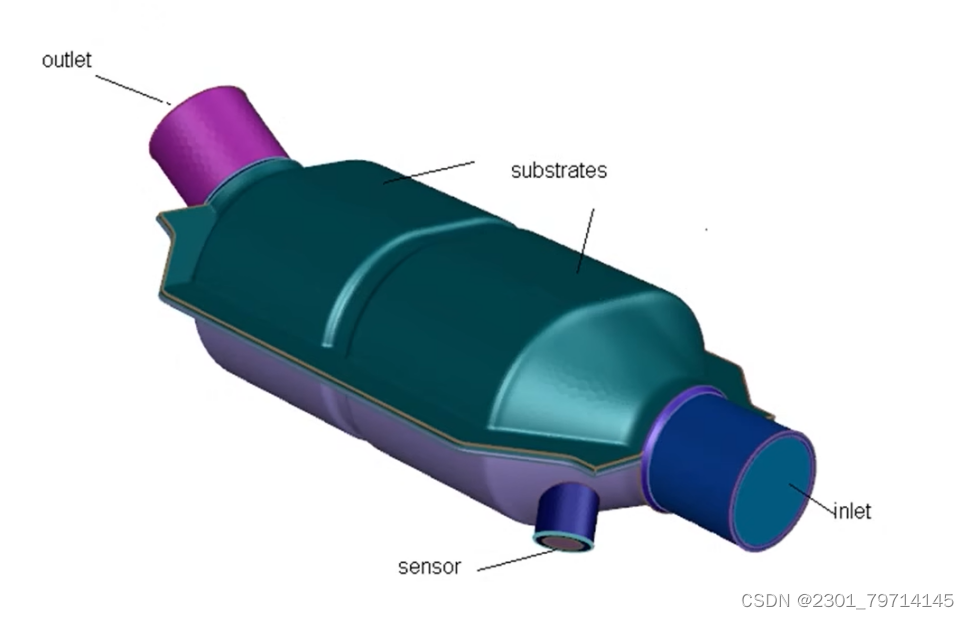
切面如下所示：

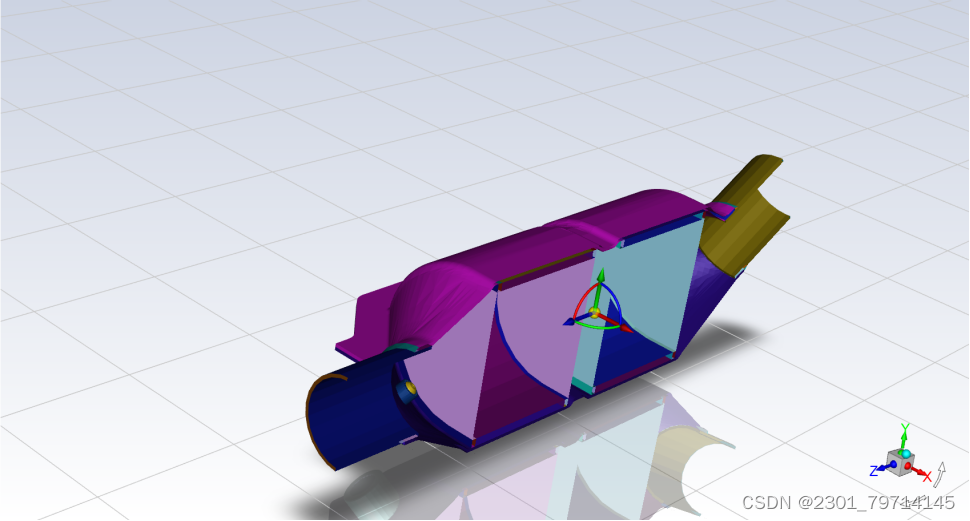
该模型中存在一个突出的传感器（sensor），会影响其流场划分，故划分网格时要对其进行加密的操作；其余区域按照曲率进行划分网格即可：

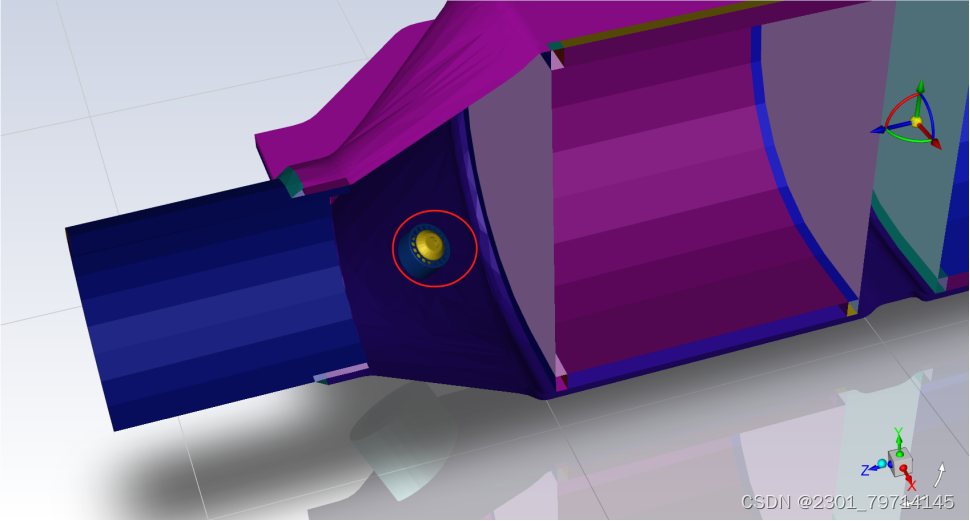
网格划分部分

进入meshing后，对传感器部分进行网格加密，选择添加局部尺寸，使用曲率（curvature）进行加密，最大尺寸设置为1.2mm，最小尺寸设置为0.1mm具体设置如下所示：

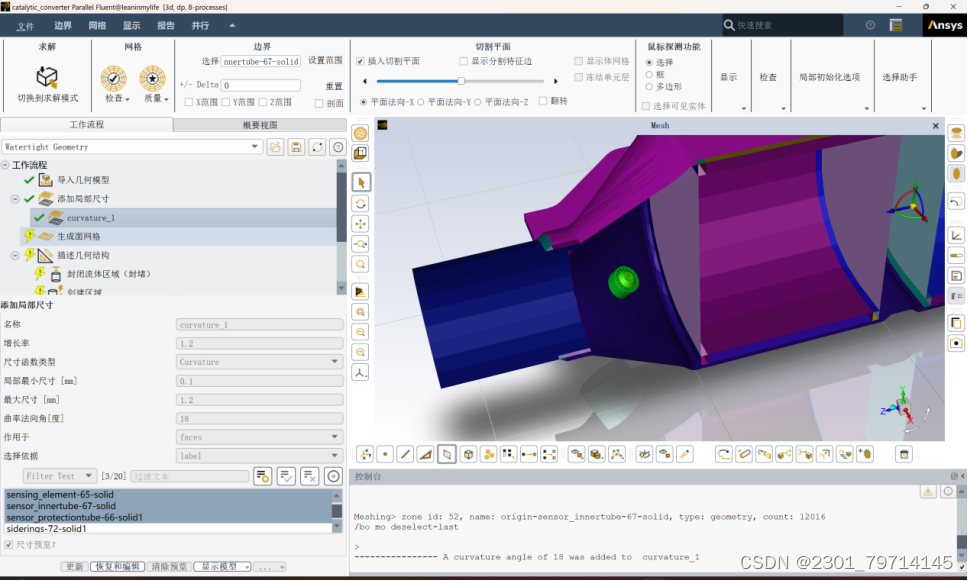
进行面网格的划分，将最小尺寸调大至1.5mm，来减少网格数量，在高级选项中将质量改进的限制值改为0.95，对超过0.95质量的网格进行优化，减少计算资源，提升运算效率。生成效果如下：

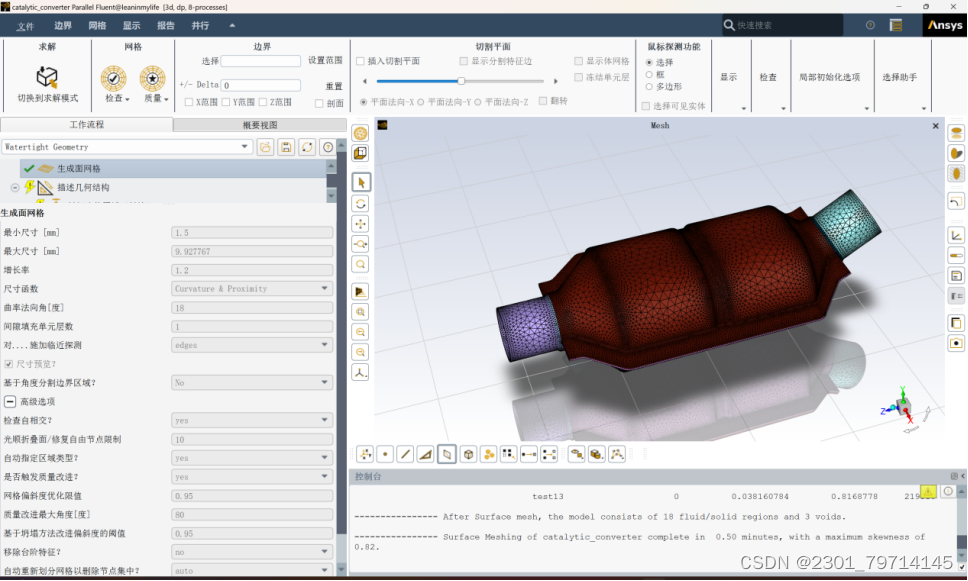
可从切面看出，传感器部分网格加密划分效果：

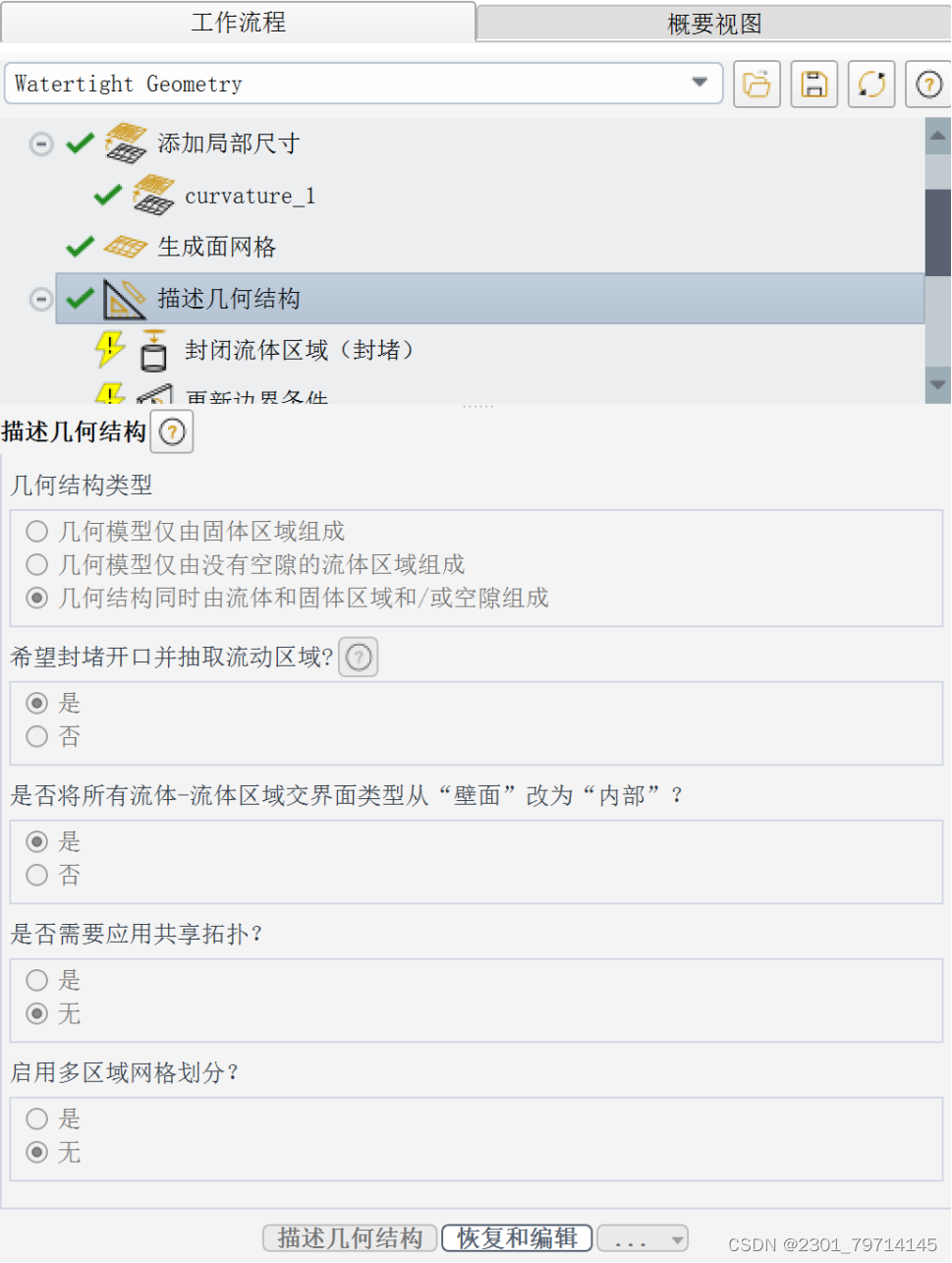
后对几何结构进行描述，该模型为一个有固体域与流体域的模型，选择同时存在固体、流体和空隙的选项。由于该模型只存在固体区域的开口，并没有流体区域的封口，选择封堵流体区域来进行对流体区域的封口。存在多孔介质，在fluent中视多孔介质为流体区域，故选将流体-流体的选择中改为是，使得区域通畅：

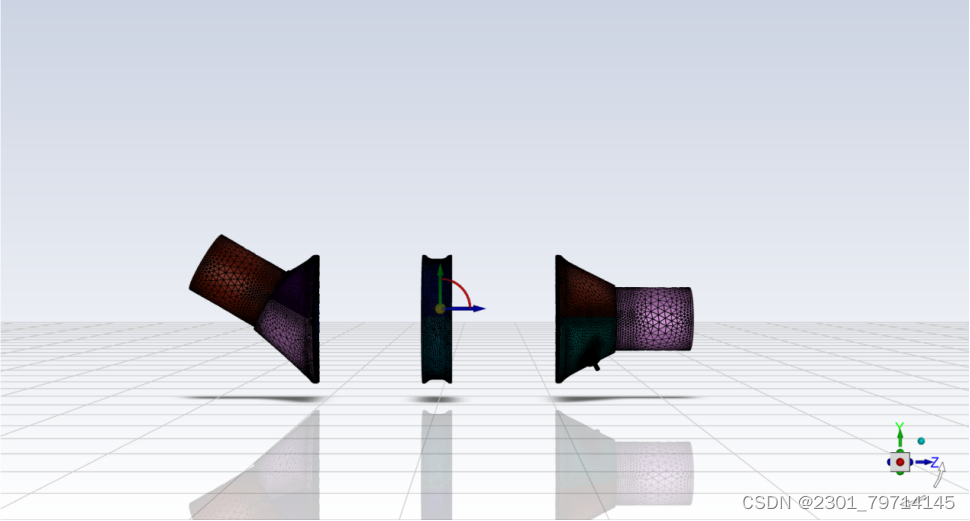
后对进出口进行封堵：

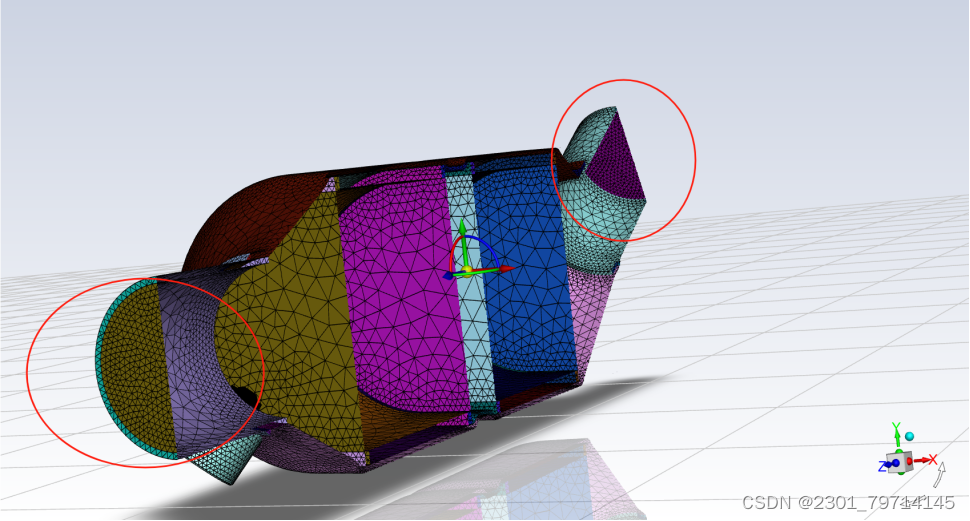检查边界条件，发现未出现划分错误的情况，更新完边界条件后，创建3个流体区域，可实际模型中多孔介质之间并未完全相连，故实际上有五个流体区域，但案例中表明为3个，流体区域如下所示：

在质量改进部分中，将蜂窝介质改为流体区域：

添加边界层和体网格部分保持默认，网格划分结果如下：

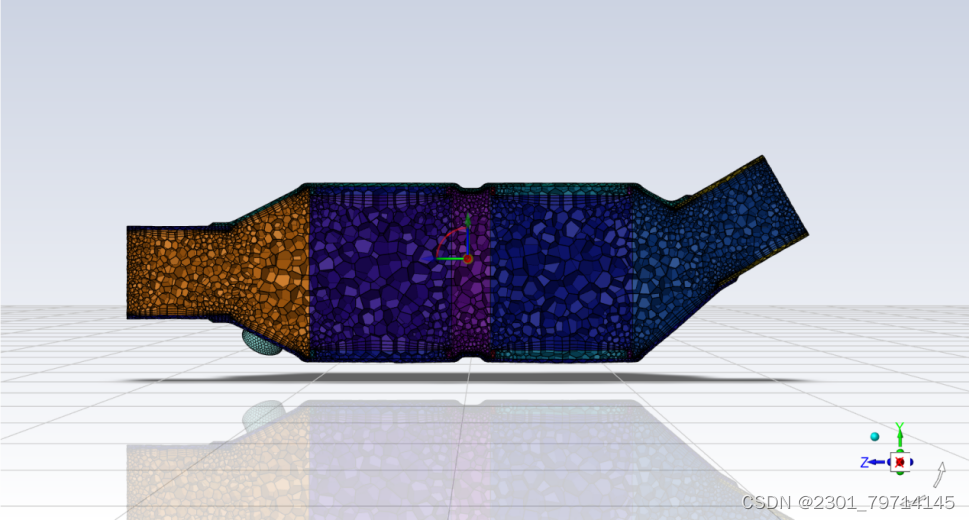
求解器部分

采用K-Omega sst模型，与k-epsilon模型相比，该模型在预测平衡逆压力流动方面更有优势，但在尾流区域和自由剪切流中稳定性较差。SST使其可以针对流体与壁面区域的情况进行针对式的选择，在进壁面区使用k-omega，在远壁面区使用k-epsilon。开启能量方程：

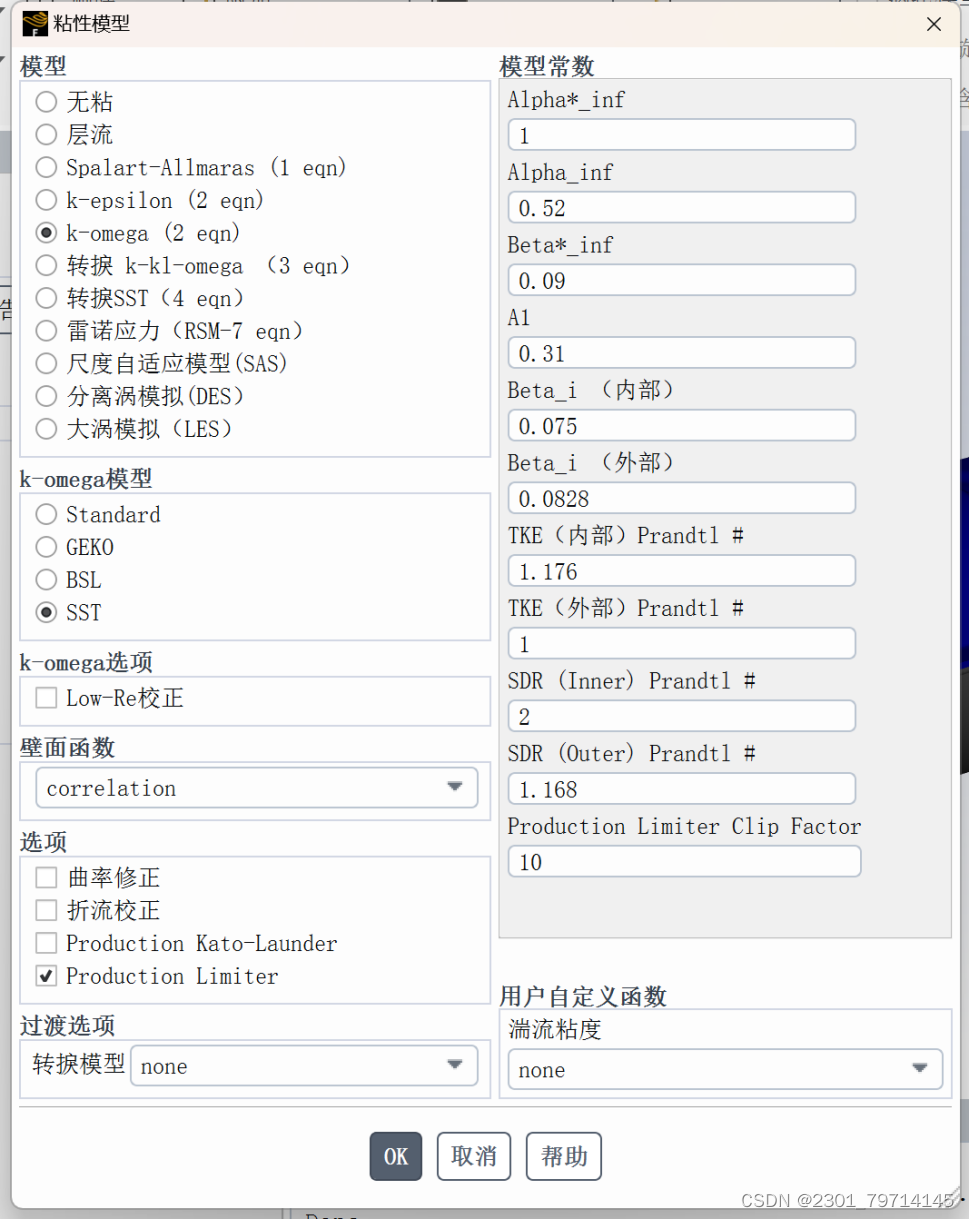
材料选择为氮气，并设置到流体区域中，对于多孔介质区域，在其中的流体是以层流的状态进行流动，需将层流区域和多孔区域的选项打开：

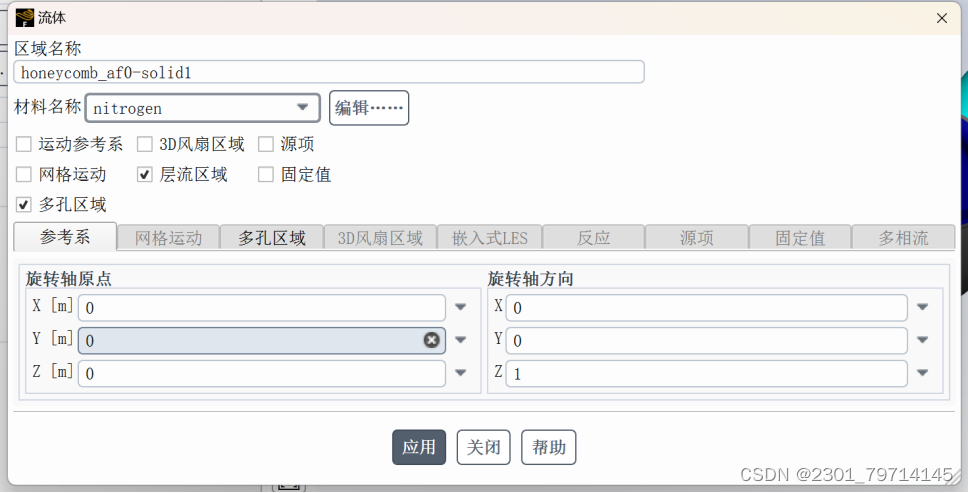
且对于多孔介质，需输入两个方向的矢量，其孔洞的径向需同坐标轴保持一致，在该案例中，Z方向上上的粘性阻力明显小于其余两个方向，输入参数至求解器中：

对进出口区域进行边界条件设置，入口速度为125m/s，湍流属性改为湍流强度和水力直径，水力直径为0.5m，强度为5%，设置温度为800k：

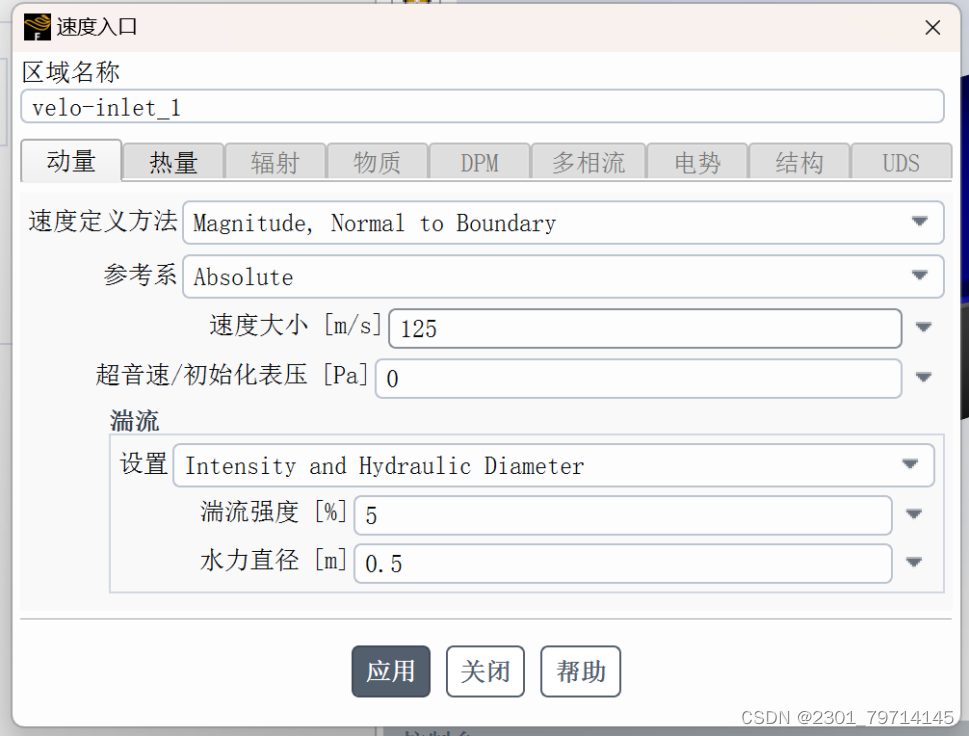
出口部分，湍流属性和温度同入口。求解方法保持默认，对出口流量进行监控，选择标准初始化，计算位置为入口。迭代步数为150次，计算结果如下：

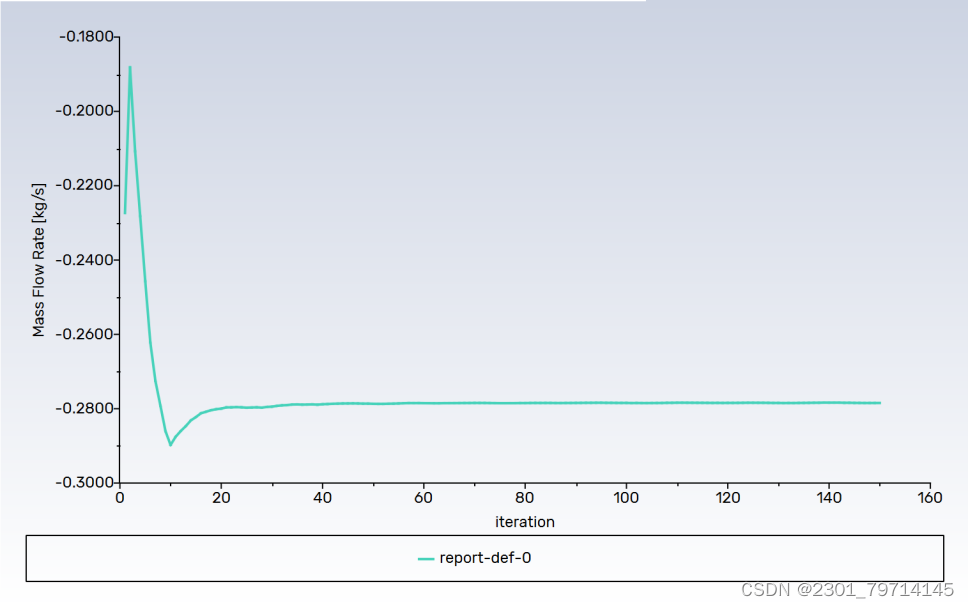
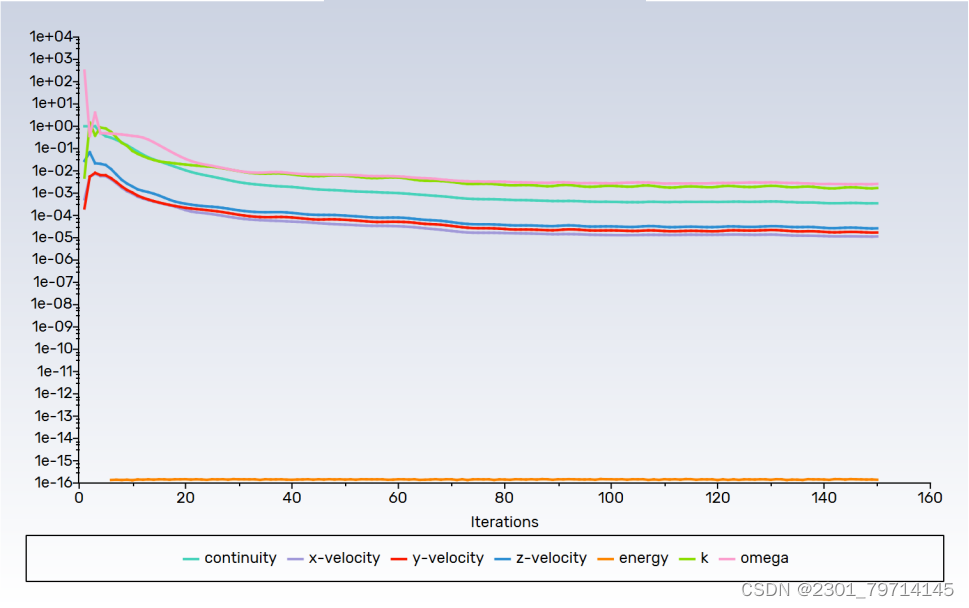
残差：

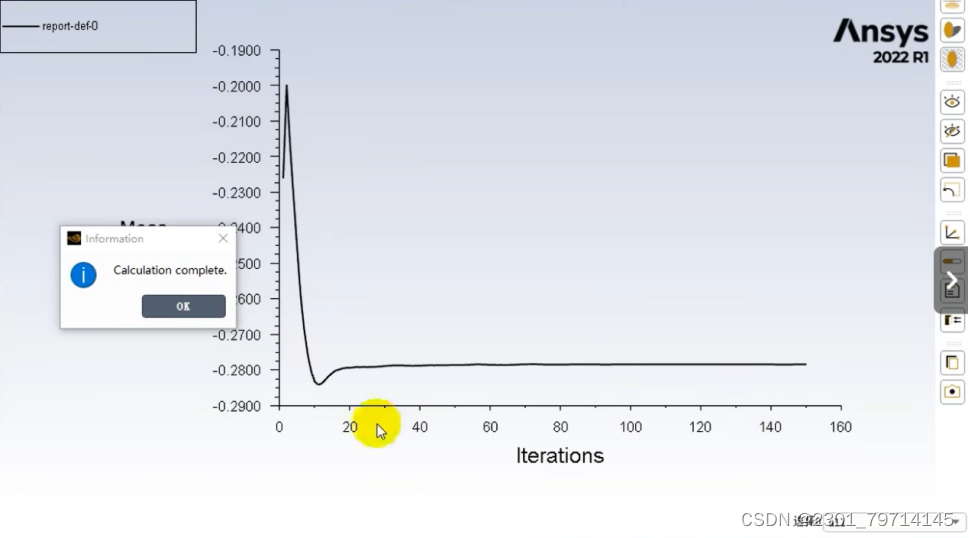
原案例计算：

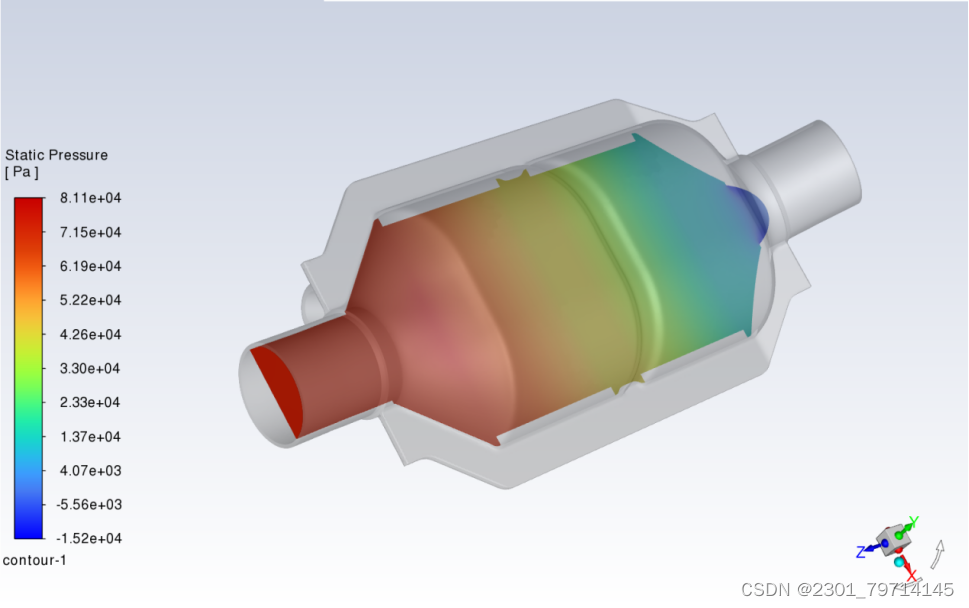
压力图：

速度迹线图：

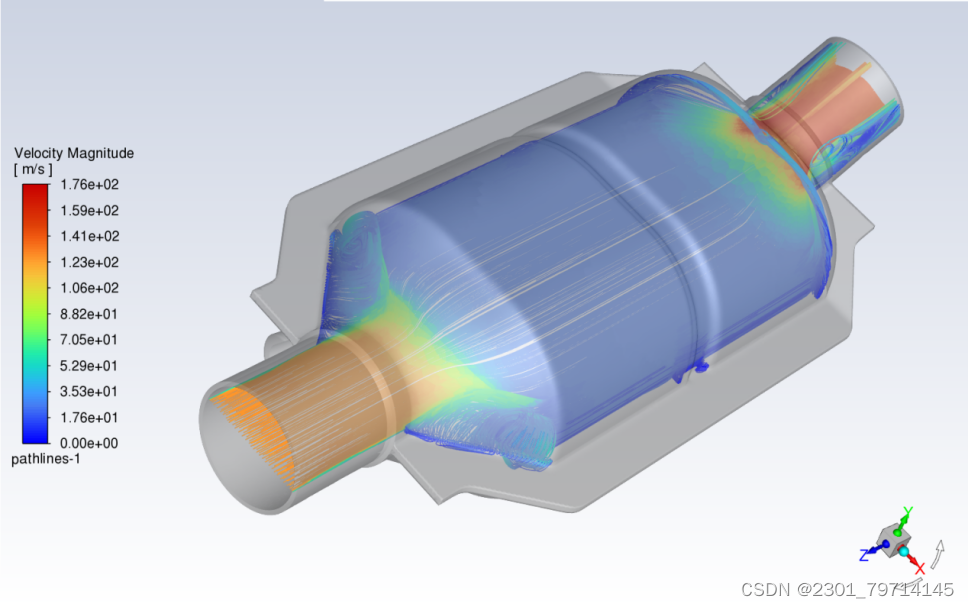
理论学习部分

总结

本周通过阅读了PINN的综述，了解到PINN在处理尾流、生物流体力学、超音速流中的应用，但由于本人知识有限，无法做到很好的总结，故选择一篇尚能理解的文章进行解读，在Fluent案例里，明白了多孔介质在Fluent中如何进行划分才不会产生计算错误，下周将会对水力学理论知识部分向下学习，希望早日获得突破。