写了一个Megatron-LM的3D Parallel进程组可视化的Playground，界面长下面这样：

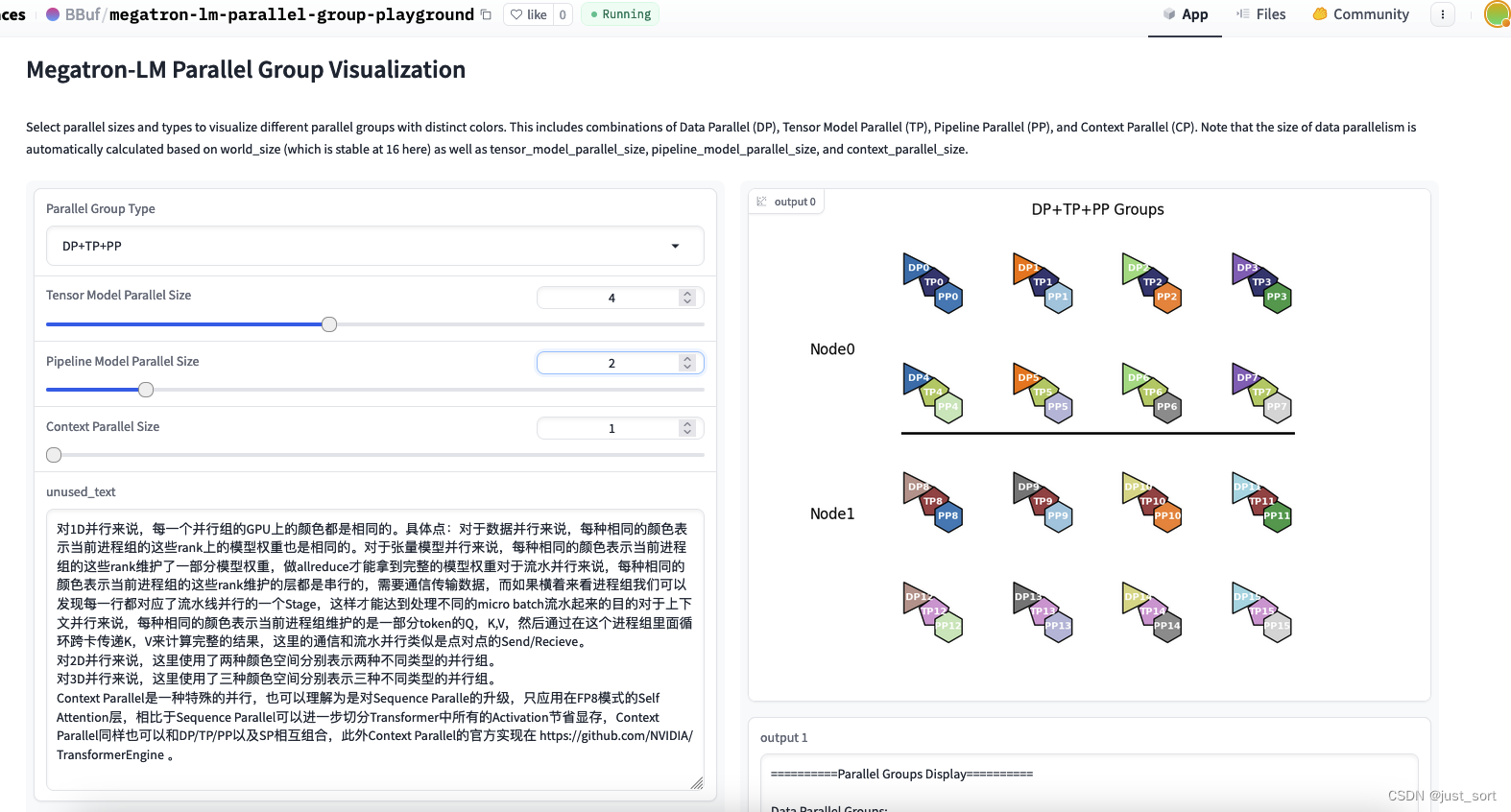
可以直接访问：https://huggingface.co/spaces/BBuf/megatron-lm-parallel-group-playground

脚本也开源在：https://github.com/BBuf/megatron-lm-parallel-group-playground 请随意获取和修改。

0x0. 前言

本次阅读一篇Megatron-LM的README贴出的一篇paper，是NVIDIA在2022年上传的，讲的是Megatron-LM里面的Sequence Parallel和Selective Activation Recomputation如何降低大语言模型训练中的激活内存。这里来看一下理论讲解，另外Paper的第4节的激活内存公式估计比较有用。paper链接为：https://arxiv.org/pdf/2205.05198.pdf 。序列并行目前是非常常用的，但是选择性激活重计算可能用得人不多，我想一个很重要的原因应该是 FlashAttention 的出现大大降低了激活值内存大小。但这篇Paper的一些公式仍然是有用处的，至少给我们提供了理论依据。此外，Meagtron-LM推出的Context Parallel是在Sequence Parallel的基础上更近一步，可以继续降低激活值的大小，并且支持更长的序列。

摘要就是说通过Sequence Parallel和Selective Activation Recomputation可以减少激活重计算，把Sequece Parallel和Tensor Parallel结合在一起基本可以避免激活重计算的需要。然后在高达一万亿参数规模的语言模型上评估了上面的两个方法，并展示了这里的放大把激活内存降低了5倍，同时把激活重计算的执行时间开销减少了超过90%。例如，在2240 NVIDIA A100 GPUs上训练一个530B参数的GPT-3风格模型时，实现了54.2%的MFU，比使用重计算实现的42.1%快了29%。

0x1. 介绍

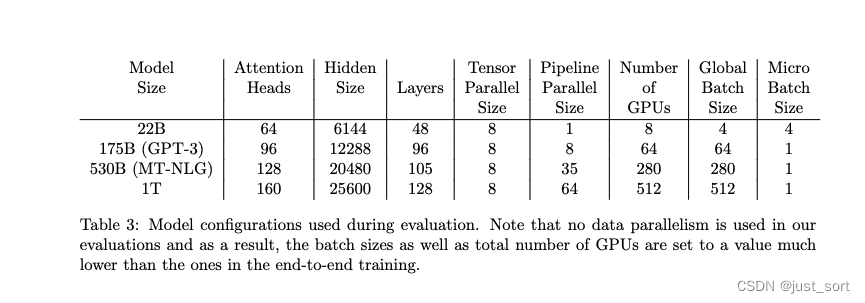
这里简单总结一下，一般来说Meagtron-LM里面张量并行都是放在同一个GPU的节点里面，节点内部由NVLink连接。然后，流水线并行虽然可以减少存储模型参数和优化器状态的内存，但是由于要存储一些Micro Batch的激活，所以并不能减少激活需要的内存。因此，激活内存的存储成为了训练大语言模型的一个关键问题。图1显示了从220亿参数到1万亿参数的四种模型配置所需的内存（模型配置的详细信息在表3中提供）。

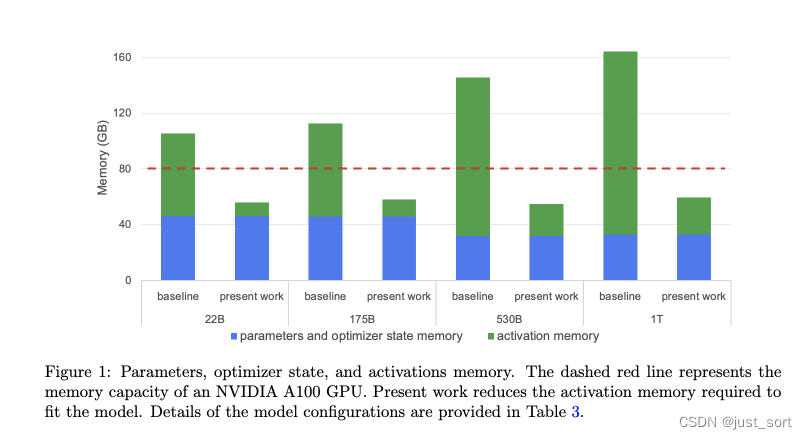
这里的present work就是通过激活重计算（也叫Gradient Checkpointing）来减轻Activation的存储大小。之前标准的做法是在每一个Transformer层的边界进行重计算，paper也把这种方法叫作完全激活重计算。但完全激活重计算会导致增加30-40%左右的时间开销。为了节省这部分计算开销，但又要Scale Up模型，所以就引入了Paper介绍的两种方法Sequence Parallel和Selective Activation Recomputation。

0x2. 相关工作rt

对Megatron-LM的张量并行进行了简单的介绍，没什么干货，忽略。

0x3. Transformer的结构

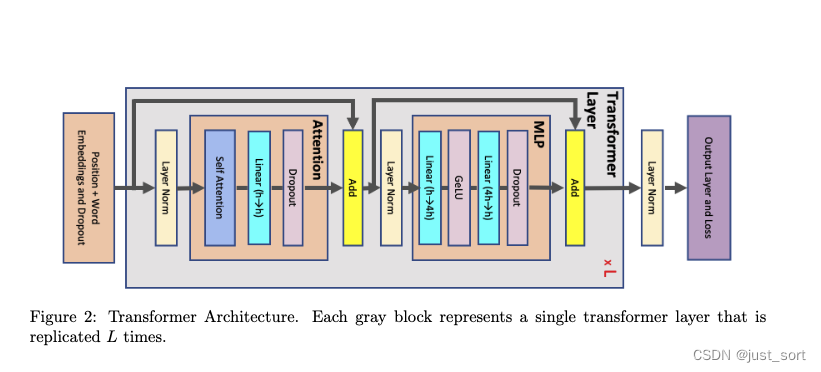
如下图的图2所示：输入token被送入一个大小为$v\times h$的词嵌入表中，token嵌入与学习到的位置嵌入（大小为$s\times h$）结合，其中$s$是序列长度，$h$是隐藏维度，$v$是词表大小。嵌入层的输出，即Transformer块的输入，是一个大小为$s\times b\times h$的3维张量，其中$b$是微批量大小。每个Transformer层由一个自注意力块组成，该块有$a$个注意力头，接着是一个增加隐藏大小到$4h$然后再减少回$h$的两层多层感知器（MLP）。每个Transformer层的输入和输出大小相同，为$s\times b\times h$。最后一个Transformer层的输出被投影回词汇维度以计算交叉熵损失。paper假设词嵌入和输出层权重是共享的。变量名在表1中列出以供参考。

0x4. Activation Memory

首先，Paper导出了一个近似的公式来估计激活内存的大小，这里的激活指的是在Forward过程中创建并且在Backward中用于梯度计算所必需的任何张量。然后，这里只考虑对激活内存贡献最大的部分不考虑小的Buffer，比如对于LayerNorm来说，输入包含bsh个元素，但均值和方差每个只有sb个元素，由于h一般很大，所以bsh远远大于2sb，所以就忽略掉2sb，以sbh来计算LayerNorm层的激活大小。

0x4.1 每个Transformer层的Activation估计

注意Paper发表的时候还没有FlashAttention。

如上图2所示，每个Transformer层由一个注意力层和一个MLP块组成，两者通过两个LayerNorm链接。下面，paper到处来存储每个元素激活所需的内存：

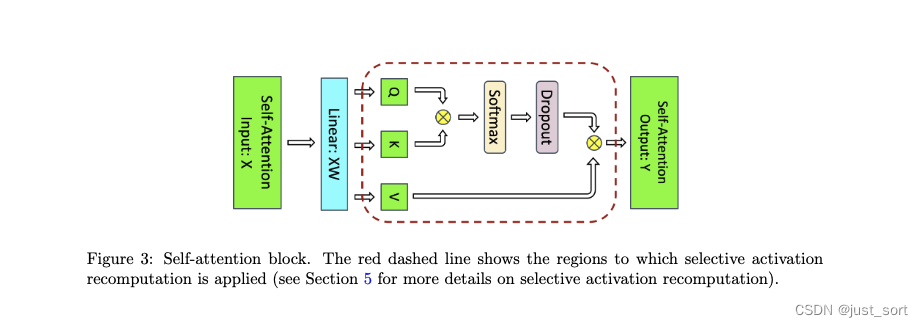
• Attention块。包括自注意力机制后跟一个线性投影和一个注意力dropout。线性投影存储其输入激活，大小为2sbh，而注意力dropout需要一个大小为sbh的掩码。如图3所示的自注意力包含几个元素：
  • 查询（Q）、键（K）和值（V）矩阵乘法：我们只需要存储它们共享的输入，大小为$2sbh$。
    QKT矩阵乘法：它需要存储Q和K，总大小为$4sbh$。
  • Softmax：反向传播需要大小为$2a{s}^{2}b$的Softmax输出。
  • Softmax dropout：只需要一个大小为$a{s}^{2}b$的掩码。
  • 对值（V）的注意力：我们需要存储dropout输出（$2a{s}^{2}b$）和值（$2sbh$），因此需要$2a{s}^{2}b+2sbh$的存储空间。
    将上述值相加，总的来说，注意力块需要$11sbh+5a{s}^{2}b$字节的存储空间。

• MLP块。两个线性层存储它们的输入，大小为$2sbh$和$8sbh$。GeLU非线性也需要其大小为$8sbh$的输入以进行反向传播。最后，dropout存储其掩码，大小为$sbh$。总的来说，MLP块需要$19sbh$字节的存储空间。
• LayerNorm。每个LayerNorm存储其输入，大小为$2sbh$，因此总共我们将需要$4sbh$的存储空间。

将注意力、MLP和层LayerNorm所需的内存相加，存储单层Transformer网络激活所需的内存是:

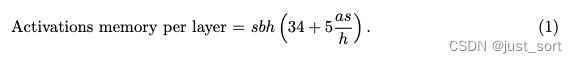
这是在没有应用模型并行时的计算公式，也就是单张卡需要的激活内存计算大小。

0x4.2 模型并行

这一节量化了张量并行对每个Transformer层的激活内存的影响。然后引入了序列并行的新方法，进一步减少了每一层的激活所需内存。最后还讨论了Pipline并行对激活内存的影响，并推导了激活内存的理论公式。

0x4.2.1 张量并行

指的就是Megatron-LM的张量并行，如下图所示：

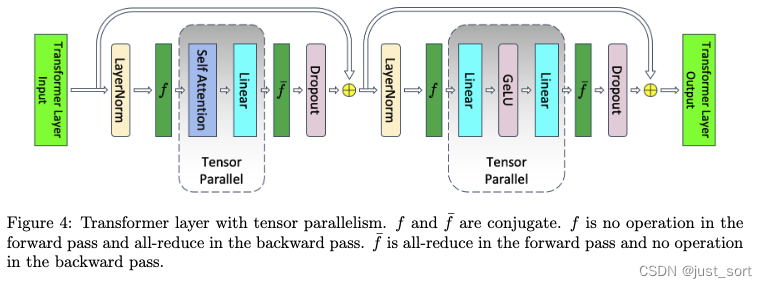
然后应用了张量并行之后上面的公式就变成：

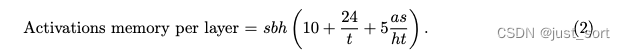
这里的10分别表示两个LayerNorm的输入，以及SelfAttention和MLP模块的输入以及输出部分Dropout所需要的激活内存。

0x4.2.2 序列并行

Megatron-LM序列并行的原理就是下面这张图，对比图4来看我们可以发现在非Tensor Parallel的部分使用了Sequence Parallel，同时通信原语也发生了变化：

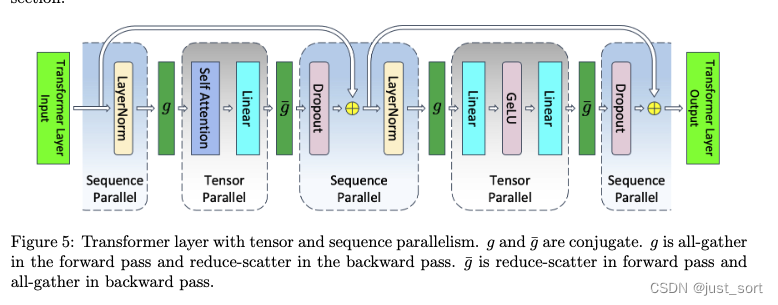
在Figure4中，由于LayerNorm和Dropout必须接收完整的数据，对于一个Transformer Layer来说前向和后向都分别有2次all-reduce。而在序列并行中，前后向的2次allreduce分别被拆成了allgather+reduce-scatter，总的通信量没发生变化。paper在这一节对此有一个证明，这里就忽略了，直接给出同时使用序列并行和Tensor并行下的激活内存计算公式：

和单纯的张量并行相比，现在两个LayerNorm的输入，以及SelfAttention和MLP模块的输入以及输出部分Dropout所需要的激活内存都减少了$t$倍，因为按照序列的维度进行了切分。

0x4.2.3 Pipline并行

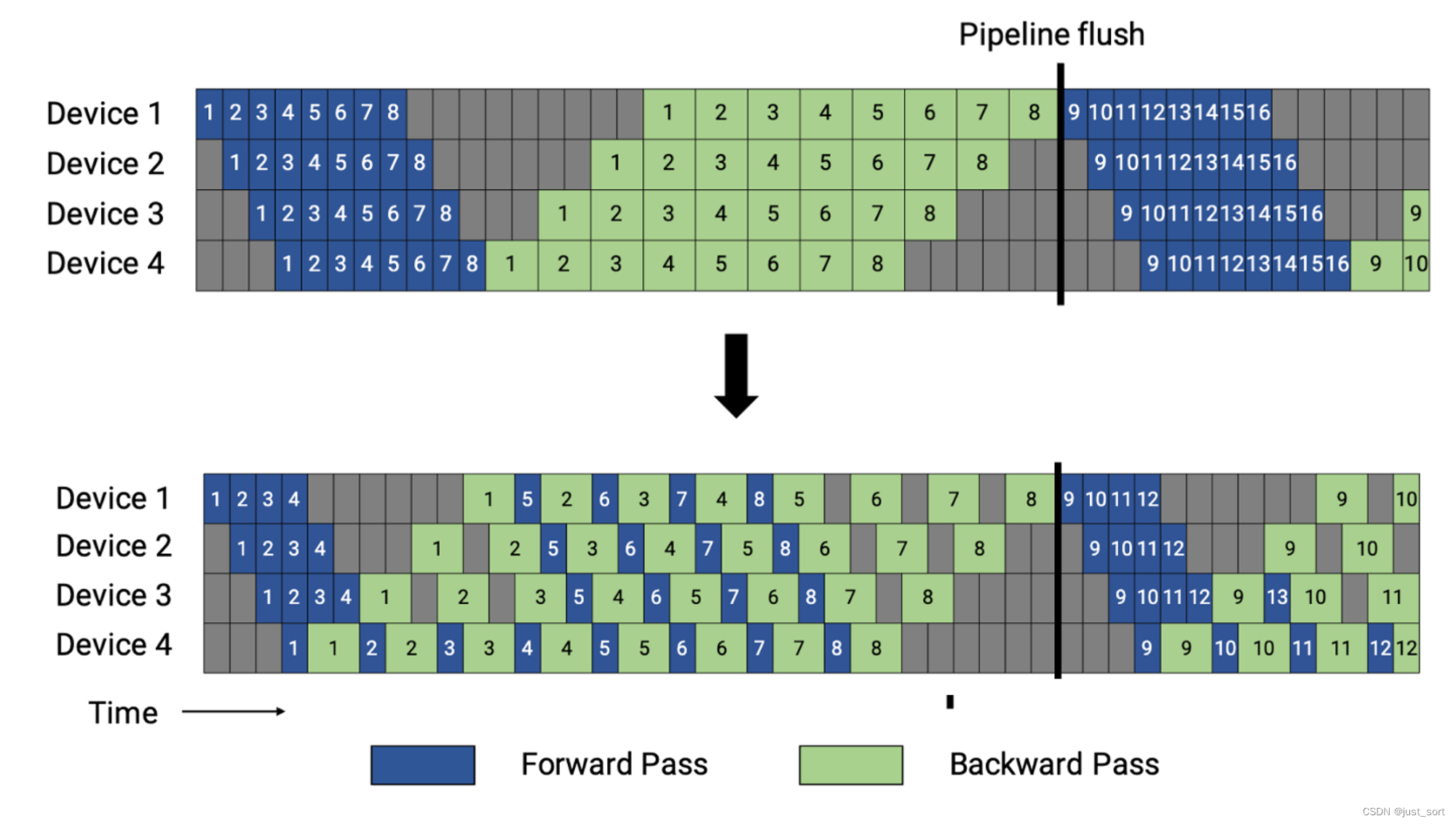
Pipline并行可以读我之前写的这篇paper解读：AI Infra论文阅读之将流水线并行气泡几乎降到零（附基于Meagtron-LM的ZB-H1开源代码实现解读）。在这篇文章里面提到过对于GPipe来说流水线中最长驻留了 $m$ 个未完成的 micro batch（上半部分图）. 而 1F1B 则限制其最多驻留流水线深度 $p$ 个未完成的 micro batch，如此形成了上图中的下半部分的流水线。这个流水线的特点是一个迭代的时间没有变化，但是 $p\ll m$ ，所以驻留的未完成的 micro batch极大减少，减少了显存峰值。（重点是减少了显存的峰值，但是气泡还是不变）。这也是下图为什么估计第一个Stage的激活内存时分子乘以了L的原因，而和micro bacth的大小无关。

对于VPP来说，公式有一些变化，第一个Stage的显存会增加。

0x4.3 总的激活内存

上面的公式5没有考虑输入嵌入，最后一层的LayerNorm以及如图2所示的输出层所需的激活内存。位置和词嵌入在反向传播中不需要存储任何大量的激活内存。但Dropout操作需要激活内存。嵌入层中的Dropout也沿序列维度并行化。因此，它将需要$sbhp/t$的存储空间。这里的p是Pipline并行维度，以及我们需要存储$p$个micro batch的事实。
输出层之前的LayerNorm也使用序列并行，因此需要$2sbh/t$的存储空间。输出层投影到词汇维度需要$2sbh/t$的存储空间。最后，交叉熵损失需要存储以32位浮点数计算的对数值，因此将需要$4sbv/t$的存储空间。总共$4sbh/t(1+v/h)$，仅在没有Pipline并行的情况下包括（$p=1$）。
加上上述内存，由输入嵌入、最后一层LayerNorm和输出层引起的额外激活内存公式是：

$\frac{sbhL}{t}\left(\frac{p}{L}+{\delta }_{p=1}\frac{4}{L}\left(1+\frac{v}{h}\right)\right)$

其中，${\delta }_{p=1}$在p=1时为1，否则为0。实际上这里的额外激活相比于公式5来说就太小了，例如对于22B的模型来说，额外激活的占比只有0.01%，所以一般直接用公式5估计激活内存就比较准确了。

0x5. 选择性的激活重计算

这一节翻译一下原文。

公式5得出的所需总激活内存对于大型模型来说仍然可能相当大。通过存储（或“checkpointing”）一组层的输入激活并在反向传播期间使用额外的前向pass重计算其它所需激活，激活重计算[5]克服了这一内存限制（这在本文中被称为完全激活重计算）。假设组只包含单个层，并忽略Transformer层外的激活，这种方法将激活所需的总内存减少到2sbhL。我们注意到，如果我们只在每个张量并行等级中存储部分激活，则这个所需内存可以进一步减少到2sbhL/t。然而，这种方法需要每层额外进行一次全收集操作，并将增加通信开销，因此，我们不考虑这种方法。

与存储所有激活（公式5）相比，对所有Transformer层进行checkpointing显著减少了训练模型所需的内存量。这种减少确实以重新计算（一个额外的前向pass）的成本为代价，可能引入高达30-40%的计算时间开销。为了平衡内存节省和计算开销，理想情况下应该只checkpointing足够的激活，以允许给定的模型并行配置在设备内存的限制下进行训练。序列并行性提供的内存节省使得许多更多的配置能够在无需重计算的情况下进行训练，但大型模型的最佳模型并行配置通常仍需要保存和重计算一些激活。选择存储与重计算激活数量的一个简单方法是只对一些Transformer层进行检查点，并存储其它层的所有激活。这种方法对大型模型的扩展性不是很好；例如，在训练MT-NLG时，每个设备只有三层，限制了你在内存与计算之间平衡的粒度。此外，我们注意到，并非所有激活都需要相同数量的操作来重新计算，因此，更加明智地选择哪些激活要存储和哪些需要重计算是有益的。

我们提出的不是对整个Transformer层进行checkpointing和重新计算，而是只对每个Transformer层中占用大量内存但重计算计算成本不高的部分进行checkpointing和重计算，或称为选择性激活重计算 。为此，我们注意到，公式5中的$5as/h$项是由于网络宽度通过计算Q、K和V值的线性层增加后的注意力操作所致；即，$Q{K}^T$矩阵乘法、softmax、softmax dropout和对V的注意力操作。这些操作通常具有大的输入大小，因此激活量大，然而，每个输入元素的浮点操作数（FLOPs）非常低。Transformer层的其余部分占据了公式5中的$34$项。因此，对于大型模型，其中$5as/h>34$，如果我们checkpointing并重新计算Transformer层的这一部分，我们存储的激活几乎可以少一半，并且重计算那些未存储的激活只有一个相对不高的成本。

使用这种形式的选择性激活重计算，存储激活所需的内存从公式5减少到：

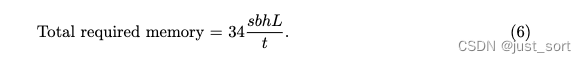
上述公式展示了，使用选择性激活重计算允许所需的激活内存与序列长度线性比例增长，并且独立于注意力头的数量。正如第4.2.3节中讨论的，在使用VPP Schedule的情况下，上述公式需要乘以$1+\frac{p-1}{pm}$。

在使用Pipline并行时，如第4.2.3节讨论的，尽管给定设备只有$L/p$层，但第一个Stage仍必须存储相当于L层激活的量，因为它必须为$p$个micro batch存储Activation来流水。在这种情况下，可以采用的另一种技术是尽可能根据可用设备内存存储尽可能多的micro-batch的所有激活，并对其余部分进行完全或选择性重计算。实践中我们发现，应用序列并行和选择性激活重计算后，重计算开销足够小，以至于这种额外技术提供的改进非常有限。这种技术在附录C中有更详细的描述和分析。

简而言之，通过选择性激活重计算，可以有效减少存储激活所需的内存，使其与序列长度线性相关，而与注意力头数量无关。尤其在使用管道并行性时，采用额外技术进一步降低重计算成本是可能的，但在实际应用中，序列并行性和选择性激活重计算已经能够显著降低重计算开销，使得额外技术的效果较为有限。

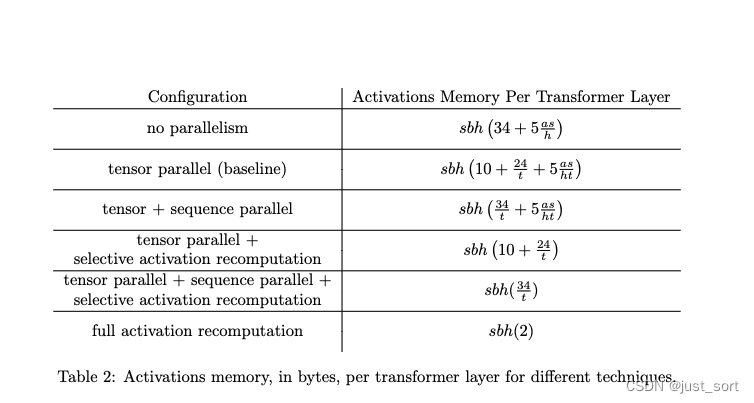
这一节的Table2值得注意一下，是对上面各种并行和重计算方式的中间激活内存的计算公式。

0x6. 实验部分

Table3展示了进行试验的几个模型的尺寸大小和超参数。

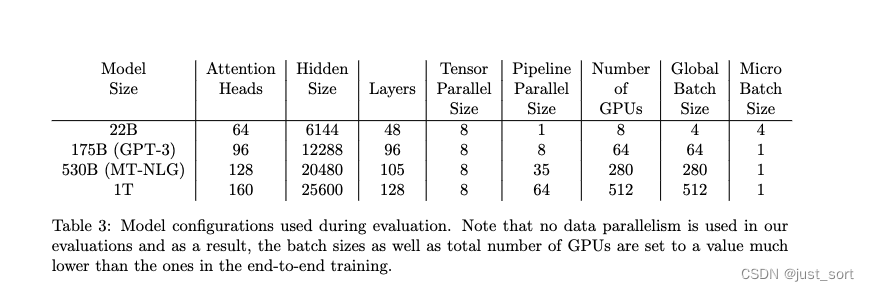
然后实验部分看下几个图和表格就可以了。

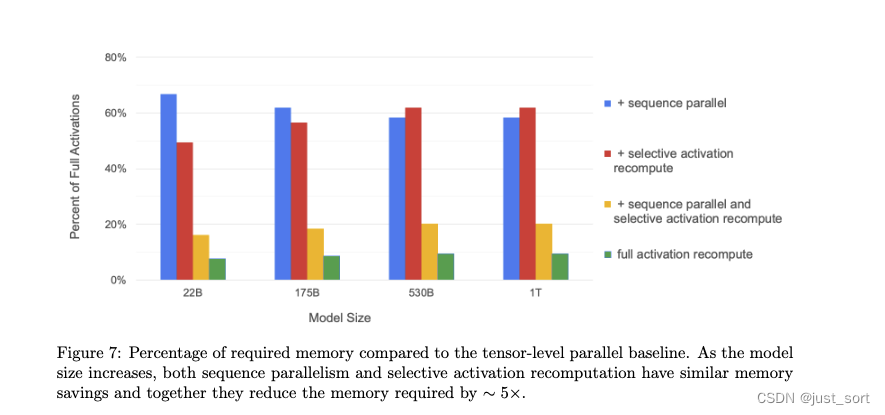
这张图是实测了下相比于单纯的模型并行，Sequence Parallel，Selective Recompute，Full Compute等能节省的显存比例，可以看到序列并行和选择性重计算很有作用。

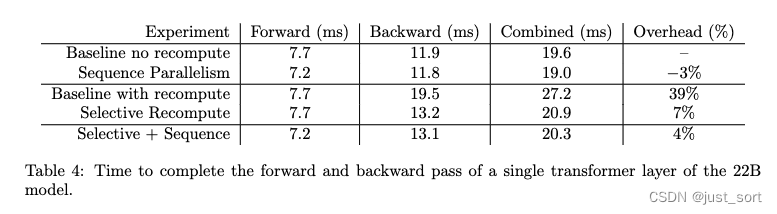
Table4展示了序列并行和选择性重计算分别对前后向时间的影响，是在22B的模型上实验的，可以看到序列并行和选择性重计算同时作用的情况下也只增加了4%的overhead。

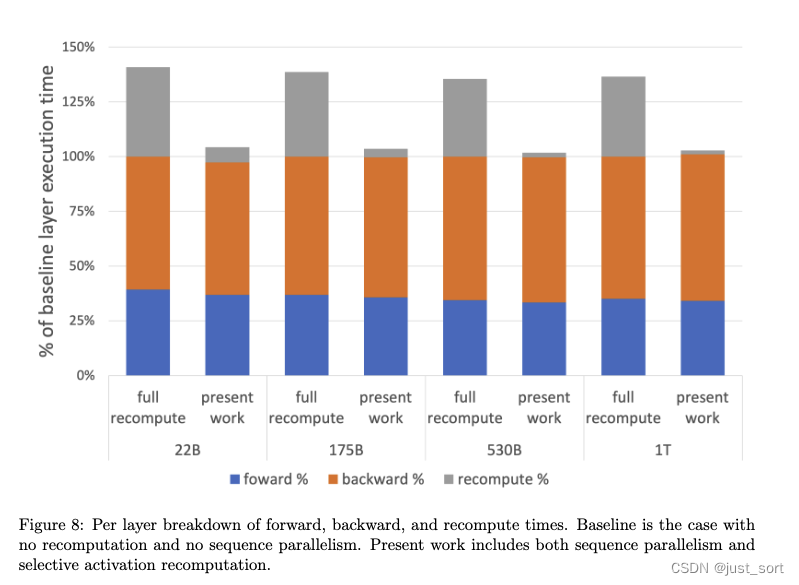
这张图的结论就是序列并行和选择性重计算相比于完全重计算来说增加的算力开销非常少。

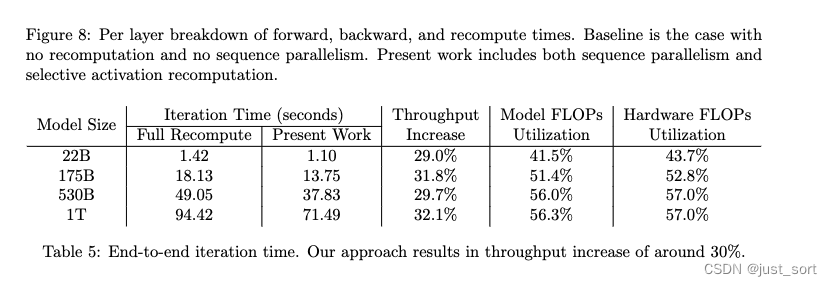
通过序列并行和选择性重计算可以提升各个尺寸大模型的吞吐和MFU。

0x7. 结论

序列并行目前是非常常用的，但是选择性激活重计算可能用得人不多，我想一个很重要的原因应该是FlashAttention的出现大大降低了激活值内存大小。但这篇Paper的一些公式仍然是有用处的，至少给我们提供了理论依据。此外，Meagtron-LM推出的Context Parallel是在Sequence Parallel的基础上更近一步，可以继续降低激活值的大小，并且支持更长的序列。