目录
一、理论
1、初步引入
2、做简化
3、拉普拉斯修正
二、实战
1、计算P(c)
2、计算P(x|c)
3、实战结果
1、数据集展示
2、相关信息打印
一、理论
1、初步引入
在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
个人通俗地理解:给一些这个西瓜的信息x(eg:纹理如何?色泽如何?),计算这个西瓜是好瓜的概率和是坏瓜的概率,比较大小,哪个概率较大,该西瓜就属于哪一类
理解转为公式:就是找
2、做简化
1)贝叶斯转换
由贝叶斯公式可以将 做如下转换:
2)针对目标简化:
我们最终是要确定使得最大的
,而
对任何
都一致,所以求
可以舍去分母,也即求
对于 和
采用估计
3)求P(c)
假定训练集数据容量足够且分布能够真实反应数据实际时,我们可以将频率估计为概率
即
4)求P(x|c_i)
a)x是离散属性
令 表示
中在第i个属性上取值为xi的样本组成的集合,则条件概率
可估计为
b)x是连续属性
通常对条件概率不能用频率估计,一般采用的方式:先假定其具有某种确定的概率分布形式,再基于训练样本对概率分布的参数进行估计。
假设 服从正态分布,
其中:
3、拉普拉斯修正
问题:若某个属性值在训练集中没有与某个类同时出现过,则直接将概率连乘,会导致“哪怕在其他属性上明显像好瓜,分类的结果都将是坏瓜”的情况。
为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”,在估计概率值时通常要进行“平滑”(smoothing),常用“拉普拉斯修正”(Laplacian correction)
具体做法是:
二、实战
1、主要流程介绍:
1)完整代码:
DrawPixel/Bayesian_decison.ipynb at main · ndsoi/DrawPixel (github.com)
2)实战分三个部分:

详情可以见上述链接,博文只放关键代码
1、计算P(c)
1)先从数据集中找出类别为c的所有数据
def getDc(train_data,Class):
Dc = []
for melon in train_data:
if melon['类别'] == Class:
Dc.append(melon)
return Dc然后只需用以下计算Pc
Pc = len(Dc)/len(train_data)收集好的Dc可以进一步用于计算 P(x|c)
2、计算P(x|c)
1)离散属性
写出求 类别c中属性attr取值为value的样本概率
# 计算类别c中属性attr取值为value的样本概率
def calP_xiForI(attr,value,Dc):
cnt = 0
for melon in Dc:
if melon[attr] == value:
cnt+=1
#print(f"P(({attr}={value})|{melon['类别']})={cnt/len(Dc)}")
return cnt/len(Dc)计算 对于给定的一个样本test('attr1':'value1','attr2':'value2',..,),已知它所有的属性,则它是类别Class的概率【这里仅考虑离散属性】
def calPcx(train_data,Class,test):
# 找出类别为Class的数据
Dc = getDc(train_data,Class)
Pc = len(Dc)/len(train_data)
# print(f"P({Class})={Pc}")
ans = 1
for attr,value in test.items():
# 属性是离散的
tmp = calP_xiForI(attr,value,Dc)
ans*= tmp
return ans*Pc2)连续属性:
对于连续属性,要先计算均值和方差:
import math
### 计算均值
def calmu_c_i(Dc,attr):
mu = 0
for data in Dc:
mu += float(data[attr])
print(f"attr={attr},mu={mu/len(Dc)}")
return mu/len(Dc)
### 计算方差
def cal_sigma_c_i(Dc,attr):
sigma = 0
mu = calmu_c_i(Dc,attr)
for data in Dc:
sigma+=(float(data[attr])-mu)*(float(data[attr])-mu)
print(f"方差attr={attr}.sigma={math.sqrt(sigma/len(Dc))}")
return math.sqrt(sigma/len(Dc))然后写出计算P(x|c)的函数
def calP_xiForC(attr,Dc,test):
sigma = cal_sigma_c_i(Dc,attr)
mu = calmu_c_i(Dc,attr)
tmp = -(float(test[attr])-mu)*(float(test[attr])-mu)/(2*sigma*sigma)
return 1/math.sqrt(2*math.pi*sigma)*math.exp(tmp)
计算样本x是Class类别的概率(既考虑离散又考虑连续属性)
def calPcx_v3(train_data,Class,test,Attrs):
# 找出类别为Class的数据
Dc = getDc(train_data,Class)
Pc = len(Dc)/len(train_data)
# print(f"P({Class})={Pc}")
ans = 1
for attr,value in test.items():
# 属性是离散的
if Attrs[attr] == 'c':
tmp = calP_xiForC(attr,Dc,test)
else:
tmp = calP_xiForI_v2(attr,value,Dc)
# 属性是连续的
ans*= tmp
print(f"calPcx_v3:{ans*Pc}")
return ans*Pc3、实战结果
(复现西瓜书7.3的例题)
1、数据集展示
训练数据集:

测试例:
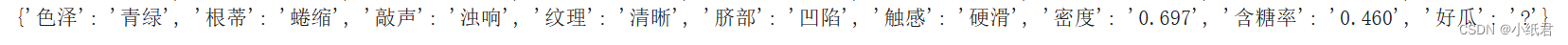
2、相关信息打印

结果解析,最上方的红色和黄色框指的是好瓜中密度的均值、方差以及含糖率的密度和均值
蓝色和绿色框指的是坏瓜中密度的均值、方差以及含糖率的密度和均值
黑色是测试集的原始数据集和预测类别,看到对于测试例的预测是“好瓜”