基于物理的实时渲染 -- PBR

简介

PBR，或者用更通俗一些的称呼是指基于物理的渲染(Physically Based Rendering)，它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。正因为基于物理的渲染目的便是为了使用一种更符合物理学规律的方式来模拟光线，因此这种渲染方式与我们原来的Phong或者Blinn-Phong光照算法相比总体上看起来要更真实一些。除了看起来更好些以外，由于它与物理性质非常接近，因此我们（尤其是美术师们）可以直接以物理参数为依据来编写表面材质，而不必依靠粗劣的修改与调整来让光照效果看上去正常。使用基于物理参数的方法来编写材质还有一个更大的好处，就是不论光照条件如何，这些材质看上去都会是正确的，而在非PBR的渲染管线当中有些东西就不会那么真实了。

这种渲染方式需要遵循以下三个条件：

基于微平面(Microfacet)的表面模型。
能量守恒。
应用基于物理的BRDF。

一、微平面模型

所有的PBR技术都基于微平面理论。这项理论认为，达到微观尺度之后任何平面都可以用被称为微平面(Microfacets)的细小镜面来进行描绘。根据平面粗糙程度的不同，这些细小镜面的取向排列可以相当不一致：
在这里插入图片描述
产生的效果就是：一个平面越是粗糙，这个平面上的微平面的排列就越混乱。这些微小镜面这样无序取向排列的影响就是，当我们特指镜面光/镜面反射时，入射光线更趋向于向完全不同的方向发散(Scatter)开来，进而产生出分布范围更广泛的镜面反射。而与之相反的是，对于一个光滑的平面，光线大体上会更趋向于向同一个方向反射，造成更小更锐利的反射：
在这里插入图片描述
我们可以基于一个平面的粗糙度来计算出某个向量的方向与微平面平均取向方向一致的概率。这个向量便是位于光线向量LigthDir和视线向量ViewDir之间的中间向量(Halfway Vector)。H向量等于标准化后的（L向量+V向量）即：H=normalize(L+V)。

二、能量守恒

微平面近似法使用了这样一种形式的能量守恒(Energy Conservation)：出射光线的能量永远不能超过入射光线的能量（发光面除外）。当一束光线碰撞到一个表面的时候，它就会分离成一个折射部分和一个反射部分。反射部分就是会直接反射开来而不会进入平面的那部分光线，这就是我们所说的镜面光照。而折射部分就是余下的会进入表面并被吸收的那部分光线，这也就是我们所说的漫反射光照。

反射光与折射光它们二者之间是互斥的关系。无论何种光线，其被材质表面所反射的能量将无法再被材质吸收。因此，诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。我们按照能量守恒的关系，首先计算镜面反射部分，它的值等于入射光线被反射的能量所占的百分比。然后折射光部分就可以直接由镜面反射部分计算得出。

三、反射率方程

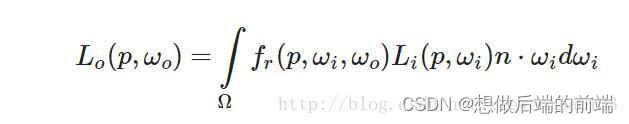
在这里插入图片描述
该函数是个连续函数所以我们需要对其进行离散化，离散化后的各个符号代表的含义如下:p表示观察点、ωo表示观察方向即出射方向、ωi表示入射方向、L表示光源颜色方程、fr表示双向反射分布函数。

3.1 辐射率方程

这个方程表示的是，一个拥有辐射通量Φ的光源在单位面积A，单位立体角ω上的辐射出的总能量：
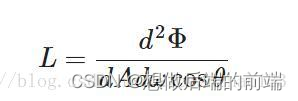
在这里插入图片描述
如果我们把立体角ω和面积A看作是无穷小的，那么我们就能用辐射率来表示单束光线穿过空间中的一个点的通量。这样我们可以计算得出作用于单个（片段）点上的单束光线的辐射率，我们实际上把立体角ω转变为方向向量ωi然后把面A转换为点p。这样我们可以直接在着色器中使用辐射率来计算单束光线对每个片段的作用了。

ps：事实上，当涉及到辐射率时，我们通常关心的是所有投射到点pp上的光线的总和，而这个和就称为辐射照度或者辐照度，辐照度公式如下。
在这里插入图片描述

vec3  lightColor  = vec3(23.47f, 21.31f, 20.79f);//我们一般用RGB代替辐射通量Φ
vec3  wi          = normalize(lightPos - fragWorldPos);//入射方向
float cosTheta    = max(dot(n, wi), 0.0f);
float attenuation = calculateAttenuation(fragWorldPos, lightPos);//光线衰减
float radiance    = lightColor * attenuation * cosTheta;

3.2 BRDF双向反射分布函数

它接受入射（光）方向ωi，出射（观察）方向ωo，平面法线n以及一个用来表示微平面粗糙程度的参数a作为函数的输入参数。BRDF可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。举例来说，如果一个平面拥有完全光滑的表面（比如镜面），那么对于所有的入射光线ωi（除了一束以外）而言BRDF函数都会返回0.0 ，只有一束与出射光线ωo拥有相同（被反射）角度的光线会得到1.0这个返回值。

我们一般使用Cook-Torrance BRDF模型：
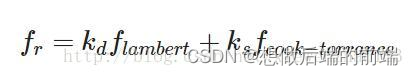
在这里插入图片描述
这里的kd是入射光线中被折射部分的能量所占的比率，而ks是被反射部分的比率。BRDF的左侧表示的是漫反射部分，这里用flambert来表示。它被称为Lambertian漫反射，这和我们之前在漫反射着色中使用的常数因子类似，用如下的公式来表示：
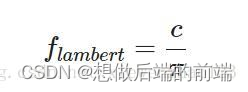
在这里插入图片描述
c表示表面颜色，除以ππ是为了对漫反射光进行标准化。

RDF的镜面反射部分要稍微更高级一些，它的形式如下所示：
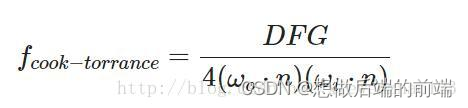
在这里插入图片描述
其中D表示正态分布函数、F表示菲涅尔方程、G表示几何函数。

正态分布函数：估算在受到表面粗糙度的影响下，取向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。
几何函数：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
菲涅尔方程：菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率

a、正态分布函数
假设给定向量h，如果我们的微平面中有35%与向量h取向一致，则正态分布函数或者说NDF将会返回0.35。
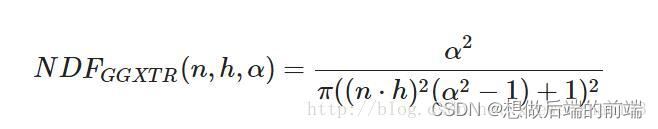
在这里插入图片描述
h表示中间向量，n表示法向量，α表示表面粗糙程度。

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a      = roughness*roughness;//这里不是很懂为什么要把从main中传递过来的粗糙度进行乘方处理
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;
	
    float nom   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;
	
    return nom / denom;
}

b、几何函数：从统计学上近似的求得了微平面间相互遮蔽的比率，这种相互遮蔽会损耗光线的能量。
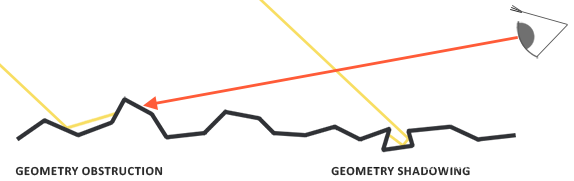
在这里插入图片描述
几何函数采用一个材料的粗糙度参数作为输入参数，粗糙度较高的表面其微平面间相互遮蔽的概率就越高。我们将要使用的几何函数是GGX与Schlick-Beckmann近似的结合体，因此又称为Schlick-GGX：

为了有效的估算几何部分，需要将观察方向（几何遮蔽(Geometry Obstruction)）和光线方向向量（几何阴影(Geometry Shadowing)）都考虑进去。我们可以使用史密斯法(Smith’s method)来把两者都纳入其中：
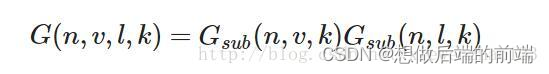
在这里插入图片描述

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;//计算K，这里是直接光照

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;
	
    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2  = GeometrySchlickGGX(NdotV, roughness);
    float ggx1  = GeometrySchlickGGX(NdotL, roughness);
	
    return ggx1 * ggx2;
}

c、菲涅尔方程：
该方程描述的是被反射的光线对比光线被折射的部分所占的比率，这个比率会随着我们观察的角度不同而不同。当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。
当垂直观察的时候，任何物体或者材质表面都有一个基础反射率(Base Reflectivity)，但是如果以一定的角度往平面上看的时候所有反光都会变得明显起来。你可以自己尝试一下，用垂直的视角观察你自己的木制/金属桌面，此时一定只有最基本的反射性。但是如果你从近乎90度（译注：应该是指和法线的夹角）的角度观察的话反光就会变得明显的多。如果从理想的角度观察，所有的平面理论上来说都能完全的反射光线。这种现象因菲涅尔而闻名，并体现在了菲涅尔方程之中。
菲涅尔方程是一个相当复杂的方程式，不过幸运的是菲涅尔方程可以用Fresnel-Schlick近似法求得近似解：
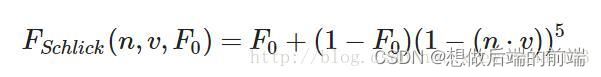
在这里插入图片描述
Fo表示平面基础反射率，N为法线向量，V为观察向量。

vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{
    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}  

void main()
{
	vec3 F0 = vec3(0.04);//平面的基础反射率
    F0      = mix(F0, albedo, metallic);//根据材质的反射率和金属程度计算较为准确的反射率
    vec3 F  = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);//菲涅尔方程计算出被反射光线的百分比
}

最终方程：
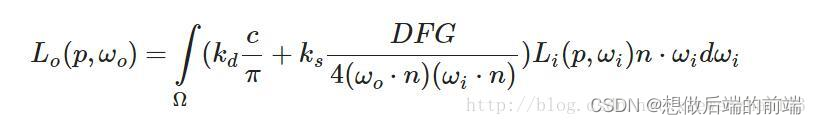
在这里插入图片描述

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// 材质参数
uniform vec3 albedo;//反射率
uniform float metallic;//金属程度
uniform float roughness;//粗糙程度
uniform float ao;//

// 灯属性
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;
  
 //正态分布函数
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a      = roughness*roughness;
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;
	
    float nom   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;
	
    return nom / denom;
}

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;
	
    return nom / denom;
}

//几何函数
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2  = GeometrySchlickGGX(NdotV, roughness);
    float ggx1  = GeometrySchlickGGX(NdotL, roughness);
	
    return ggx1 * ggx2;
}

//菲涅尔方程
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{
    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}  

void main()
{		
    vec3 N = normalize(Normal);//得到法线向量
    vec3 V = normalize(camPos - WorldPos);//得到观察方向向量

    vec3 F0 = vec3(0.04);//平面的基础反射率
    F0      = mix(F0, albedo, metallic);//根据材质的反射率和金属程度计算较为准确的反射率
    vec3 F  = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);//菲涅尔方程计算出被反射光线的百分比
	
    vec3 kS = F;
    vec3 kD = vec3(1.0) - kS;
    kD *= 1.0 - metallic;	  
           
    // 反射比方程式
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // 计算每个灯光的辐射率
        vec3 L = normalize(lightPositions[i] - WorldPos);//入射光方向
        vec3 H = normalize(V + L);//得到半程向量
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);//计算衰减
        vec3 radiance     = lightColors[i] * attenuation;//衰减后的灯光     
        
        // cook-torrance brdf
		//双向反射分布函数，它接受入射（光）方向ωi，出射（观察）方向ωo，
		//平面法线nn以及一个用来表示微平面粗糙程度的参数aa作为函数的输入参数。
		//BRDF可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。
		float NDF = DistributionGGX(N, H, roughness);//正态分布函数，这是用来估算微平面的主要函数。
        float G   = GeometrySmith(N, V, L, roughness);//几何函数，从统计学上近似的求得了微平面间相互遮蔽的比率
        
		//BRDF镜面反射部分
        vec3 nominator    = NDF * G * F;//分子
        float denominator = 4 * max(dot(V, N), 0.0) * max(dot(L, N), 0.0) + 0.001;//分母 
        vec3 brdf = nominator / denominator;
            
        float NdotL = max(dot(N, L), 0.0);                
        Lo += (kD * albedo / PI + brdf) * radiance * NdotL; //得到最终的反射率方程
    }   
  
    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;
	
    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));  //gamma矫正
   
    FragColor = vec4(color, 1.0);
}