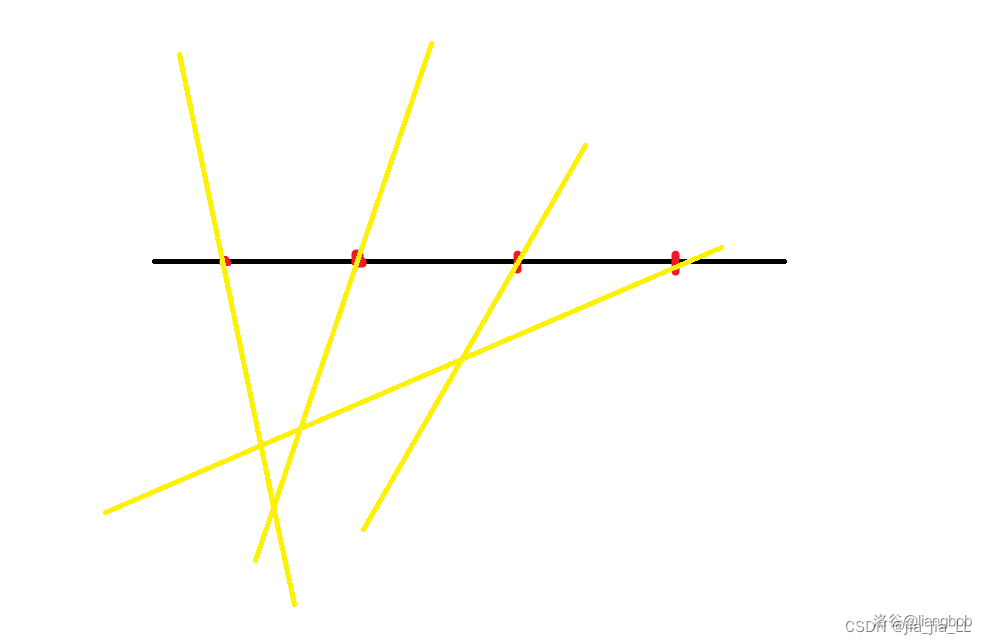
P8720 [蓝桥杯 2020 省 B2] 平面切分

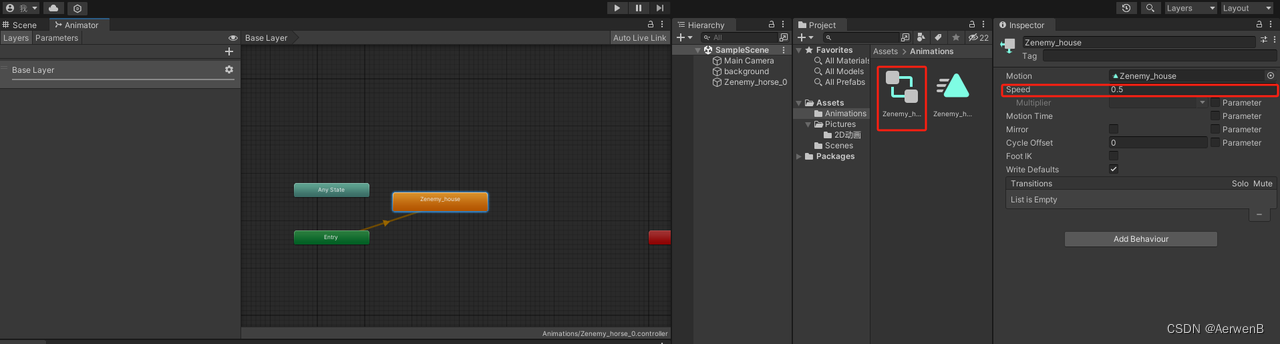
思路：首先借用dalao的图解释一下，又多出一条与当前平面任意一条直线都不重合线时，多了的平面是交点数+1，所以用双层循环每次往里面加一条直线，计算交点

#include <iostream>
#include <cstring>
#include <set>
using namespace std;
int n;
int a,b;
typedef pair<long double,long double> LD;
set<LD> II;
LD q[1010];

int main()
{
	cin>>n;
	int ans=-1;
	for(int i=0;i<n;i++)
	{
		cin>>a>>b;
		II.insert({a,b});
	} 
	for(auto i=II.begin();i!=II.end();i++)
	{
		q[++ans]={(*i).first,(*i).second};
	}
	
	int res=1;
	for(int i=0;i<=ans;i++)
	{
		set<LD> lll;
		for(int j=0;j<=i;j++)
		{
			long double k1=q[i].first;
			long double b1=q[i].second;
			long double k2=q[j].first;
			long double b2=q[j].second;
			
			if(k1==k2) continue;
			long double x=(b2-b1)/(k1-k2);
			long double y=k1*x+b1;
			lll.insert({x,y});
	    }
	    res+=lll.size();
	    res++;
	}
	cout<<res;
	return 0;
}

P8651 [蓝桥杯 2017 省 B] 日期问题

有点烦的一道题，刚开始没想闰年，想着直接几个if判断解决，浪费了快一个小时调程序

附未加闰年判断的代码

#include <iostream>
using namespace std;
int a,b,c;

int daysOfMonth[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int main()
{
	scanf("%d/%d/%d",&a,&b,&c);
	if(a>=60)
	{
		if(b>=1&&b<=12&&c<=daysOfMonth[b]) printf("19%02d-%02d-%02d\n",a,b,c);
	}
	else if(a<=59)
	{
		if(b>=1&&b<=12&&c<=daysOfMonth[b]) printf("20%02d-%02d-%02d\n",a,b,c);
	}
	
	if(c>=60)
	{
		if(a>=1&&a<=12&&b<=daysOfMonth[a]) printf("19%02d-%02d-%02d\n",c,a,b);
		if(b>=1&&b<=12&&a<=daysOfMonth[b]) printf("19%02d-%02d-%02d\n",c,b,a);
	}
	else if(c<=59)
	{
		if(a>=1&&a<=12&&b<=daysOfMonth[a]) printf("20%02d-%02d-%02d\n",c,a,b);
		if(b>=1&&b<=12&&a<=daysOfMonth[b]) printf("20%02d-%02d-%02d\n",c,b,a);
	}
	return 0;
}

思路：这个数据范围三种循环也不会t，所以就这样直接判断，还有记得根据年份转换一下二月份的天数

#include <iostream>
using namespace std;
int a,b,c;
int daysOfMonth[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

bool isrunnian(int x)
{
    return (x%4==0&&x%100!=0)||(x%400==0); 
}

int main()
{
	scanf("%d/%d/%d",&a,&b,&c);
	for(int i=1960;i<=2059;i++)
	{
		daysOfMonth[2]=(isrunnian(i)?29:28);
		for(int j=1;j<=12;j++)
		{
			for(int k=1;k<=daysOfMonth[j];k++)
			{
				if((a==i%100&&b==j&&c==k)||
				   (a==j&&b==k&&c==i%100)||
				   (a==k&&b==j&&c==i%100)) 
				   printf("%d-%02d-%02d\n",i,j,k);
			}
		}
	}
	return 0;
}

P8635 [蓝桥杯 2016 省 AB] 四平方和

思路：直接循环找数，让n减去其他三个数的平方和，开根号以后因为是整数，所以会丢掉小数点后的数字，利用这个判断

#include <iostream>
#include <cmath>
using namespace std;
int n;

int main()
{
	cin>>n;
	for(int a=0;a*a<n;a++)
	{
		for(int b=a;a*a+b*b<n;b++)
		{
			for(int c=b;a*a+b*b+c*c<n;c++)
			{
				int t=n-a*a-b*b-c*c;
				int d=sqrt(t);
				if(d*d==t)
				{
					printf("%d %d %d %d",a,b,c,d);
					return 0; 
				}
			}
		}
	}
	return 0;
}