几个简单的参数，实现计算特征向量的余弦相似度（java实现，纯手撸）

news2024/9/28 19:24:36

几个简单的参数，实现计算特征向量的余弦相似度（java实现，纯手撸）

太狂喽！突然高级起来🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠

1.导入

什么事相似度？
例1：
苹果和桃子？
毛桃和油桃？
明显是毛桃和油桃相似度高。

例1：
小明、小红、小亮衣服喜好分布：（1为喜欢，0为排斥）

人名	红色	黄色	蓝色	绿色	黑色	白色
小明	1	1	1	1	0	0
小红	1	0	0	0	1	1
小亮	1	1	1	1	1	0

那么我们是不是通过肉眼可分析出：
小明和小亮两人喜好相似度十分接近！因为他们喜好基本相同，只要一个不同。

😀那么我们怎么让就计算机知道他们之间的关联关系呢？

2.余弦相似度

实在不理解的同学可以看一下这个两个文章，参考一下。

链接: 余弦相似度讲解
链接: 算法实现

为什么？
其实呢~
我们只要在几何中描述出，小明的爱好的向量，小红的爱好的向量，小亮爱好的向量。
然后用小明的向量分别和小红、小亮的向量计算出余弦相似度然后哪个接近1就是更加相似。

🤒那么有聪明的小伙伴要问了，为什么是向量？为什么是余弦值？不是正弦值？

想让我们回忆一下，勾股定理！
勾股定理是什么？a²+b²=c²？是不是一秒就想到了。
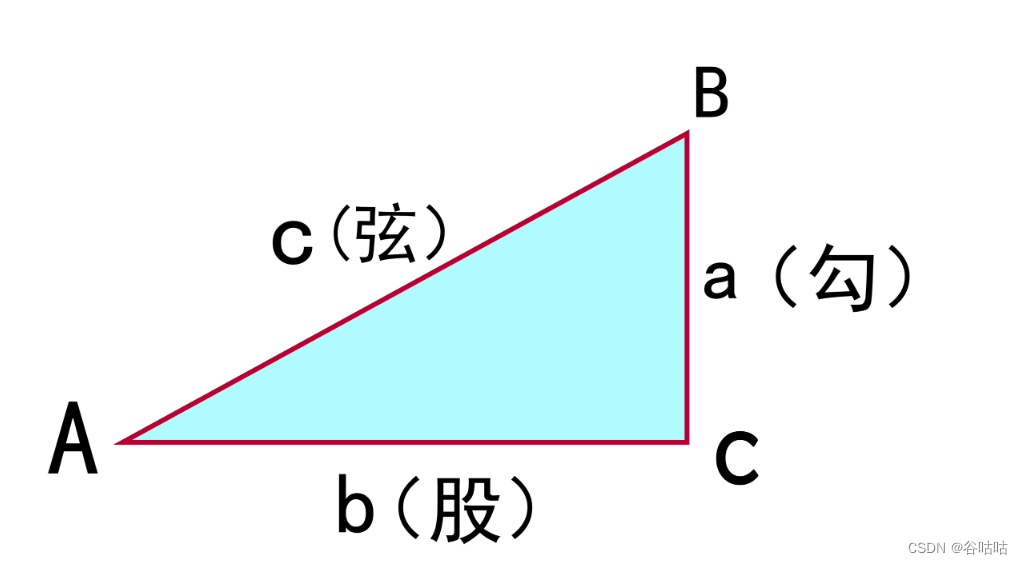
在这里插入图片描述
那么a勾作为一个向量 b作为一个向量，他们的余弦值是不是就是0了
额~回忆一下？

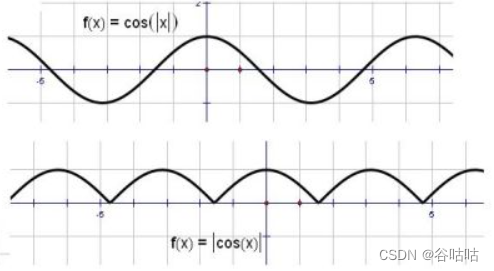
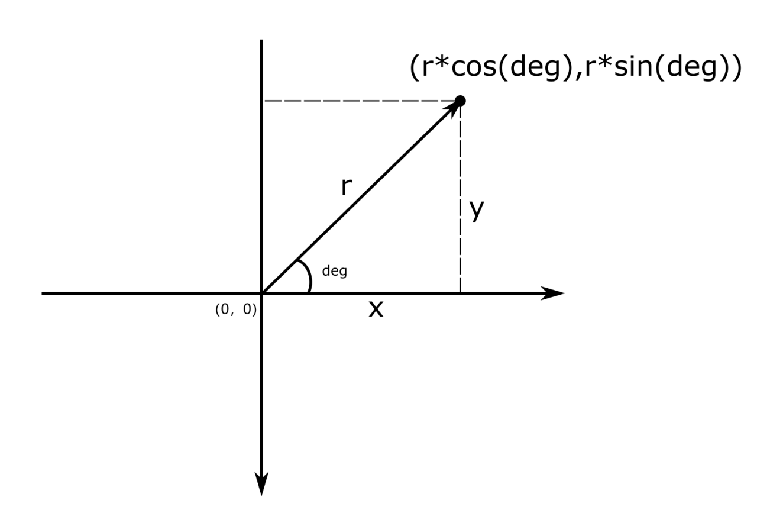
没错当x为π/2的时候也就是90°，这是的余弦值为0。
所以可以得出这两个向量的相似度非常低，当然-1的活就完全不同了，这是他的几何意义上的。

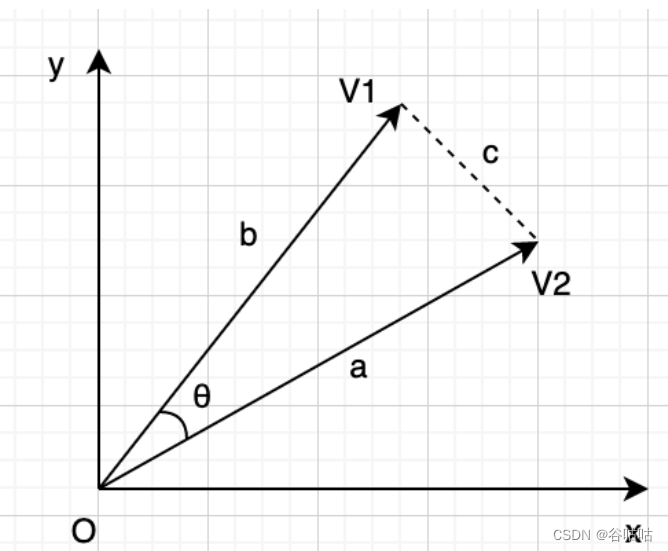
在这里插入图片描述
因为：

所以余弦值是对两个夹角大小的形容，所以靠近，夹角越小。

因为向量是通过多个特征值描述出来的一个多维度的东西。
x(红色) y（绿色） z（红色）q（黑色）p（白色）……

这样不管多少个特征值，我们都可以用向量描述出来。我们计算出夹角值就可以描述出两个向量的接近程度。

3.计算实现：

好了，终于可以计算两个向量的相似度了，拿我们上面的爱好的举例子。

例1：
小明、小红、小亮衣服喜好分布：（1为喜欢，0为排斥）

人名	红色	黄色	蓝色	绿色	黑色	白色
小明	1	1	1	1	0	0
小红	1	0	0	0	1	1
小亮	1	1	1	1	1	0

怎么计算出小明和小红的相似度呢？
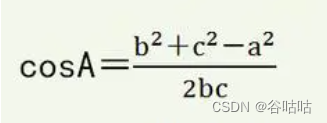
在这里插入图片描述
那么计算向量的点积

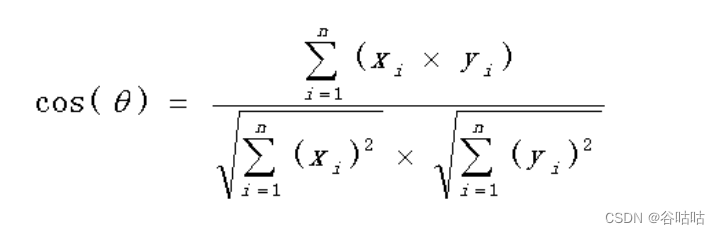
如此计算小明和小红的相似度。

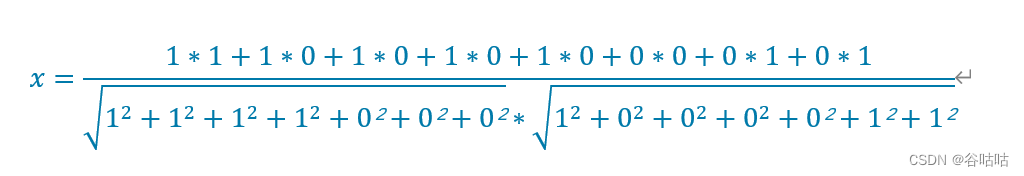
同理计算小明和小亮的相似度。
那么我们用代码实现一下
大家有其他设计上好的建议，可以在评论区回复。🫰🫰🫰🫰🫰

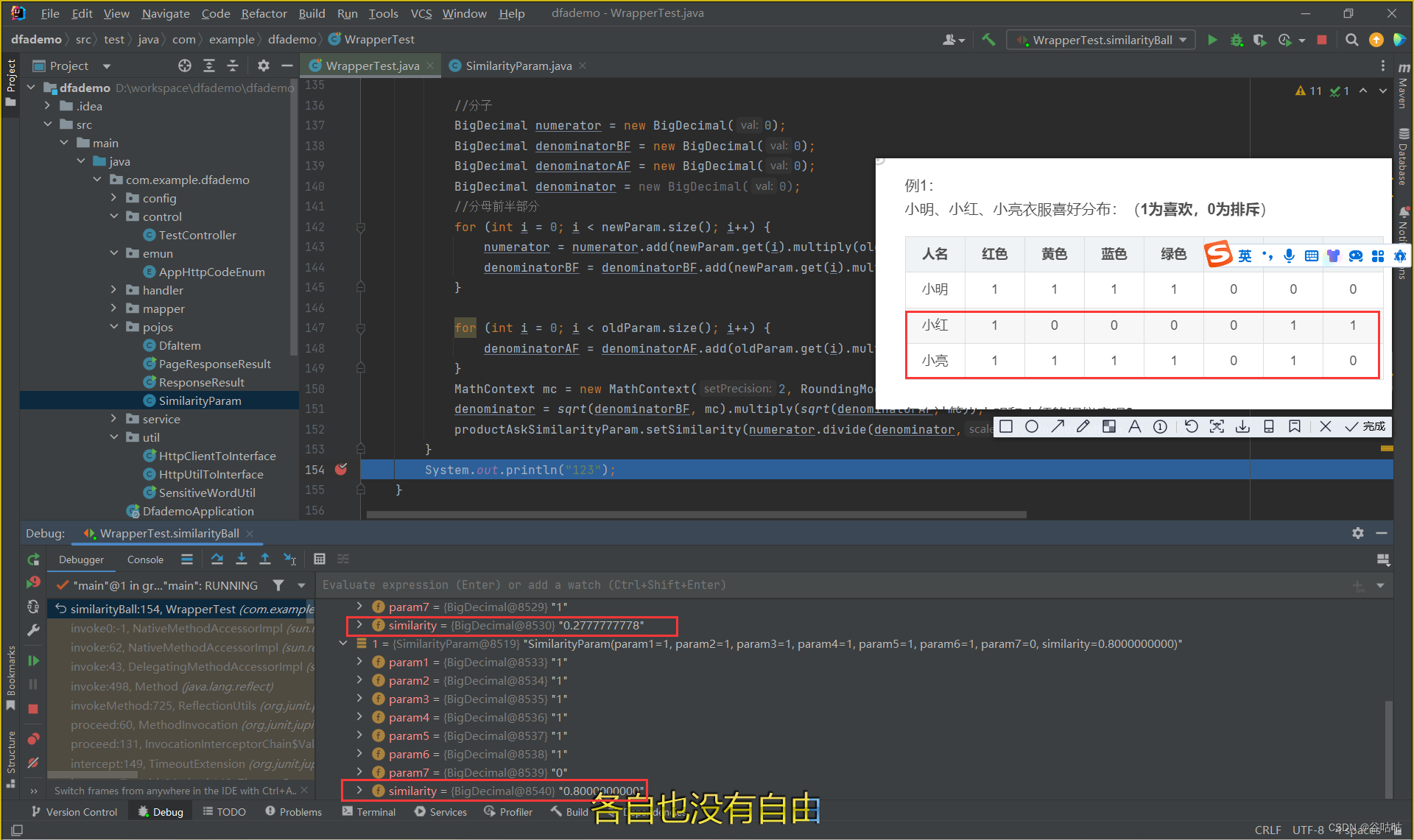
在这里插入图片描述

这里可以看到，通过计算，我们算出
小明和小红对衣服颜色的喜好相似度是0.2777777778
小明和小亮对衣服颜色的喜好相似度是0.8000000000
是不是很厉害！不愧是我🤓🤓🤓🤓🤓🤓🤓🤓🤓🤓🤓

直接给兄弟们上代码，其实大家都会写，就是懒罢了。

@Test
    public void similarityBall(){
        //计算新的小球和存量小球的余弦值，排序，取出最靠近1的。（最大的）
        SimilarityParam param = new SimilarityParam();
        param.setParam1(new BigDecimal(1));
        param.setParam2(new BigDecimal(1));
        param.setParam3(new BigDecimal(1));
        param.setParam4(new BigDecimal(1));
        param.setParam5(new BigDecimal(0));
        param.setParam6(new BigDecimal(0));
        param.setParam7(new BigDecimal(0));
        List<BigDecimal> newParam = new ArrayList<>();
        newParam.add(param.getParam1() == null ? new BigDecimal(0) : param.getParam1());
        newParam.add(param.getParam2() == null ? new BigDecimal(0) : param.getParam2());
        newParam.add(param.getParam3() == null ? new BigDecimal(0) : param.getParam3());
        newParam.add(param.getParam4() == null ? new BigDecimal(0) : param.getParam4());
        newParam.add(param.getParam5() == null ? new BigDecimal(0) : param.getParam5());
        newParam.add(param.getParam6() == null ? new BigDecimal(0) : param.getParam6());
        newParam.add(param.getParam7() == null ? new BigDecimal(0) : param.getParam7());
        List<SimilarityParam> oldAsk = getNewAsk();
        for (SimilarityParam productAskSimilarityParam : oldAsk) {
            List<BigDecimal> oldParam = new ArrayList<>();
            oldParam.add(productAskSimilarityParam.getParam1() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam1());
            oldParam.add(productAskSimilarityParam.getParam2() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam2());
            oldParam.add(productAskSimilarityParam.getParam3() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam3());
            oldParam.add(productAskSimilarityParam.getParam4() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam4());
            oldParam.add(productAskSimilarityParam.getParam5() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam5());
            oldParam.add(productAskSimilarityParam.getParam6() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam6());
            oldParam.add(productAskSimilarityParam.getParam7() == null ? new BigDecimal(0) : productAskSimilarityParam.getParam7());

            //分子
            BigDecimal numerator = new BigDecimal(0);
            BigDecimal denominatorBF = new BigDecimal(0);
            BigDecimal denominatorAF = new BigDecimal(0);
            BigDecimal denominator = new BigDecimal(0);
            //分母前半部分
            for (int i = 0; i < newParam.size(); i++) {
                numerator = numerator.add(newParam.get(i).multiply(oldParam.get(i)));
                denominatorBF = denominatorBF.add(newParam.get(i).multiply(newParam.get(i)));
            }

            for (int i = 0; i < oldParam.size(); i++) {
                denominatorAF = denominatorAF.add(oldParam.get(i).multiply(oldParam.get(i)));
            }
            MathContext mc = new MathContext(2, RoundingMode.HALF_UP);
            denominator = sqrt(denominatorBF, mc).multiply(sqrt(denominatorAF, mc));
            productAskSimilarityParam.setSimilarity(numerator.divide(denominator,10, RoundingMode.HALF_UP));
        }
        System.out.println("123");
    }

实体类

package com.example.dfademo.pojos;

import lombok.Data;

import java.math.BigDecimal;

@Data
public class SimilarityParam {
    private BigDecimal param1;
    private BigDecimal param2;
    private BigDecimal param3;
    private BigDecimal param4;
    private BigDecimal param5;
    private BigDecimal param6;
    private BigDecimal param7;
    private BigDecimal similarity;
}