蓝桥杯(2):python基础算法【上】

时间复杂度、枚举、模拟、递归、进制转换、前缀和、差分、离散化

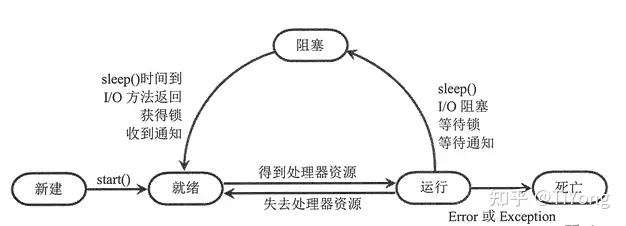
1 时间复杂度

重要是看循环，一共运行了几次

1.1 简单代码看循环

#时间复杂度1
n = int(input())
for i in range(1,n+1):
    for j in range(0,i):
        pass
###时间复杂度：1+2+3+....+n=n(1+n)/2 所以时间复杂度是o(n^2)


#时间复杂度2
for i in range(1,n+1):
    for j in range(0,n,i):
        pass
###时间复杂度：n+ n/2+ n/3+ .....+n/n = nlog(n)

1.2 复杂代码

1.2.1 归并排序

通过不断地往回带入得出的：一共带入了多少次呢？

看n可以被多少个2整除就可以个数为： $log_2^n$ ，则有 $log_2^n$ 个o(n)叠加在一起，所以复杂度为o(nlogn)

2 枚举

2.1 定义

通过逐个尝试，遍历所有的解

2.2 流程

2.3 例子

注意字符串再 in上的伟大应用！！！！

2.3.1 简单计算

a = input()
sum1,sum2=0,0
for s in a:
    if s in "aeiou":
        sum1 +=1
    else:
        sum2+=1
print(sum1)
print(sum2)

2.3.2 洁净数

问题描述：小明不喜欢数字2，包括数位上包含数字2 的数，如果没有2则称为洁净数

n = int(input())
ans = 0
for i in range(1,n+1):
    if "2" not in str(i):
        ans+=1
print(ans)

2.3.3 扫雷【初用矩阵哦】

问题描述：

#枚举
def input_list():
    return list(map(int,input().split()))


n_m = input_list()
n = n_m[0]
m = n_m[1]
a = []
for i in range(n):
    a.append(input_list())
b = [[0]*m for i in range(n)] #生成n行m列的矩阵！
# print(b)

#表示方向
dir = [(1,0),(0,1),(-1,0),(0,-1),(-1,-1),(-1,1),(-1,1),(1,1)]  #一共8个方向

for i in range(0,n):
    for j in range(0,m):
        if a[i][j] == 1:
            b[i][j]=9
        else:
            b[i][j]=0
            for k in range(8):
                x,y = i+dir[k][0],j+dir[k][1]
                if 0<=x<n and 0<=y<m:
                    if a[x][y]==1:
                        b[i][j] +=1
        print(b[i][j],end = ' ')
    print()

2.3.4 容斥定理

容斥定理：

1到n中a的倍数有 n//a 个

1到n中b的倍数有 n//b 个

1到n中ab的倍数有 n//ab 个

那么1到n中是a或者b的倍数有n//a+n//b-n//ab 个

3 模拟

3.1 定义

3.2 例题

3.2.1 喝饮料

n = int(input())
ans = n
while True:
    if n >=3:
        ans += n//3
        n = n//3+n%3
    else:
        break
print(ans)

3.2.2 像素模糊

问题描述：

像素在中间就是除以9，在别上就是除的数不定

def input_list():
    return list(map(int,input().split()))


n,m = input_list()
b = [[0]*m for i in range(n)]
a = []
dir = [(0,-1),(0,1),(-1,0),(1,0),(-1,-1),(1,-1),(1,1),(-1,1)]
for i in range(n):
    a.append(input_list())
for i in range(n):
    for j in range(m):
        count = 1
        sum_= a[i][j]
        for k in range(8):
            x,y = i+dir[k][0],j+dir[k][1]
            if 0<=x<n and 0<=y<m:
                count += 1
                sum_ += a[x][y]
        b[i][j] = int(sum_/count)
        print(b[i][j],end=' ')
    print()
#或者这样输出！！！
# for i in b:
#     print(' '.join(map(str,i)))

3.2.3 螺旋矩阵

用螺旋的方式填充矩阵！就是思考的那种形状

1 2 3 4

12 13 14 5

11 16 15 6

10 9 8 7

def input_list():
    return list(map(int,input().split()))


n,m = input_list()
x,y = 0,0
value = 1
a=[[0]*m for i in range(n)]

a[x][y]=value
print(a)
while value < n*m:
    while y+1 < m and a[x][y+1]==0:
        y = y + 1
        value += 1
        a[x][y]=value

    while x+1<n and a[x+1][y]==0:
        x=x+1
        value +=1
        a[x][y]=value

    while y-1>=0 and a[x][y-1] ==0:
        y = y-1
        value += 1
        a[x][y]=value

    while x-1>0 and a[x-1][y] == 0:
        x = x-1
        value += 1
        a[x][y]= value

for i in a:
    print(' '.join(map(str,i)))

3.2.4 对折矩阵

1 2 6 7

3 5 8 11

4 9 10 12

def input_list():
    return list(map(int,input().split()))


n,m = input_list()
a = [[0]*m for i in range(n)]
value = 1
a[0][0]=1
y,x = 0,0 # n,m
while value < n*m:

    if x+1 < m and a[y][x+1]==0:
        value += 1
        x=x+1
        a[y][x]=value

    while y+1<n and x-1>=0 and a[y+1][x-1]==0:
        value+=1
        y = y+1
        x = x-1
        a[y][x]=value

    if y+1<n and a[y+1][x] ==0:
        value +=1
        y = y+1
        a[y][x]=value

    while y-1>=0 and x+1<m and a[y-1][x+1] == 0:
        value +=1
        y = y-1
        x = x+1
        a[y][x] = value
for i in a:
    print(" ".join(map(str,i)))

4 递归

4.1 定义

4.2 汉诺塔问题

4.2.1 可以跳步的

(即可以从A直接到C)

def move(n,A,B,C):
    #n个盘子从A移动到C，借助B
    if n==0:
        return
    move(n-1,A,C,B)
    print(A,"-->",C)
    move(n-1,B,A,C)
move(3,"A","B","C")

4.2.2 不可以跳步

即只能相邻的移动，不能A直接到C

def move1(n,A,B,C):
    if n==0:
        return
    move1(n-1,A,B,C)
    print(A,"-->",B)
    move1(n-1,C,B,A)
    print(B,"-->",C)
    move1(n-1,A,B,C)
move1(2,"A","B","C")

4.3 找自然数

只需要找到n前面可以加几个数，是相同的子问题！！

代码：

def f(n):
    if n == 1:
        return 1
    ans = 1
    for i in range(1,n//2 +1):
        ans += f(i)
    return ans
print(f(6))
# 6
# 16
# 26
# 126
# 36
# 136

4.4 快速排序和归并排序

见第一节中有哦

快速排序：找基准时间复杂度0(nlogn)

def partition(a,left,right):
    stand = a[left]
    idx = left+1
    for i in range(left+1,right+1):
        if a[i]<stand:
            a[idx],a[i]=a[i],a[idx]
            idx +=1
    a[idx-1],a[left]=a[left],a[idx-1]
    #返回基准所在的位置
    return idx-1


def quicksort(a,left,right):
    if left == right:
        return a

    if left<right:
        mix = partition(a,left,right)
        quicksort(a,left,mix-1)
        quicksort(a,mix+1,right)
        return a

a = [3,4,5,6,2,1]
left = 0
right = 5
print(quicksort(a,left,right))

归并排序：

def merge(A,B):
    C=[]
    while len(A)!=0 and len(B)!=0:
        if A[0]<=B[0]:
            C.append(A.pop(0))
        else:
            C.append(B.pop(0))
    C +=A
    C+=B
    return C
# A=[1,3,5]
# B=[2,4]
# print(merge(A,B))


def merge_sort(a):

    if len(a)<2:
        return a
    mix = len(a)//2
    left = merge_sort(a[0:mix])
    right = merge_sort(a[mix:len(a)])
    a = merge(left,right)
    return a

a = [4,3 ,2,5,1]
print(merge_sort(a))

5 进制转换

5.1 基数和权

按权展开：

5.2 代码实现

5.2.1 K进制转换成10进制

int_to_char="0123456789ABCDEF"
char_to_int ={}
for idx,chr in enumerate(int_to_char):
    char_to_int[chr] =idx
print(char_to_int)
# print(char_to_int["1"])
# x = "1234"
# x = x[::-1]
# print(x)

def K_to_Ten(k,x):
    ans = 0
    x = x[::-1] #把顺序颠倒了
    for i in range(len(x)):
        ans = ans + char_to_int[str(x[i])] * k**i
    return ans

k = 8
x = "3506"
print(K_to_Ten(k,x))

5.2.2 十进制转任何进制

代码：

int_to_char="0123456789ABCDEF"
char_to_int ={}
for idx,chr in enumerate(int_to_char):
    char_to_int[chr] =idx

def Ten_to_k(k,x):
    ans = ""
    while x !=0:
        ans = ans + int_to_char[x%k]
        x = x//k
    return ans[::-1]

k=2
x=19
print(Ten_to_k(k,x))

5.2.3 任意进制之间的转换

以十进制作为桥梁

def k_k(m,n,x):
    #m进制转n进制，数字是x现在
    #第一步：m进制转10进制
    int_to_char = '0123456789ABCDEF'
    char_to_int = {}
    for idx,char in enumerate(int_to_char):
        char_to_int[char] = idx
    x = str(x)[::-1]
    y = 0
    for i in range(len(x)):
        y = y+char_to_int[str(x[i])]*m**i
    #第二步：十进制转n进制
    z = ""
    while y!=0:
        z = z+int_to_char[int(y)%n]
        y = y//n
    z = z[::-1]
    return z

m = 2
n = 16
x = 10010
print(k_k(m,n,x))

6 一维前缀和(区间)

6.1 定义

前缀和的目的是：快速求出去区间之和！

6.2 代码实现前缀和

def get_presum(a):
    n = len(a)
    sum = [0]*n
    sum[0] = a[0]
    for i in range(1,n):
        sum[i] = sum[i-1]+a[i]
    return sum

print(get_presum([1,2,3,4,5]))

6.3 前缀和实现区间差

def get_sum(sum,l,r):
    if l==0:
        return sum[r]
    else:
        return  sum[r] - sum[l-1]

a = [1,2,3,4,5]
sum = get_presum(a)
print(sum)
b = get_sum(sum,1,4)
print(b)

6.4 具体例题

6.4.1 例题1求k次方的和

注意题目中说的："请对每一个查询输出一个答案，答案对10的9次方+7取模"的意思是：答案对10的9次方+7 取余数！！【NO！！！不是的】请看下面的文章！！！

编程语言中，取余和取模的区别到底是什么？ - 知乎 (zhihu.com)

取余和取模在都是正数的时候结果相同，但是到符号不同的时候会出现不同：

取余，遵循尽可能让商向0靠近的原则

取模，遵循尽可能让商向负无穷靠近的原则

原则的解释可见：负数取余mod_负数mod运算规则-CSDN博客

综上所述：蓝桥杯里出现取模的话：！！！你就这么写：

((sum[r]-sum[l-1])+mod)%mod

def input_list():
    return list(map(int,input().split()))

mod =1000000007
def ger_presum(a):

    n = len(a)
    sum = [0]*n
    sum[0]=a[0]
    for i in range(1,n):
        sum[i] = (sum[i-1]+ a[i])%mod

    return sum


def get_sum(a,l,r):

    if l==0:
        return a[r]
    else:
        return ((a[r]-a[l-1])+mod)%mod


n,m = input_list()
a = input_list()
sum_list = []
for i in range(1,6):
    tmp_a = [x**i for x in a]
    sum_list.append(ger_presum(tmp_a))

for j in range(m):
    l,r,k = input_list()
    print(get_sum(sum_list[k-1],l-1,r-1))

6.4.2 平衡串

区间的统计都可以看作是前缀和！！！！当一个问题套三层循环的时候时间复杂度就太高了，容易不通过！

输出的最长平衡串的意思是：找到最长子串，所以基本的思想就是：遍历左端点再遍历右端点

def get_presum(a):
    n = len(a)
    sum = [0]*n
    sum[0] = a[0]
    for i in range(1,n):
        sum[i] = sum[i-1]+a[i]
    return sum


def get_sum(a,l,r):
    if l==0:
        return a[r]
    else:
        return a[r]-a[l-1]

s = input()
n = len(s)
a = []
for i in s:
    if i=="L":
        a.append(1)
    else:
        a.append(-1)
sum  = get_presum(a)
ans = 0
for i in range(0,n):
    for j in range(i,n):
        if get_sum(sum,i,j) == 0:
            ans = max(ans,j-i+1)
print(ans)

7 二维前缀和(矩阵)

7.1 定义

7.1.1 sum[i][j]之和

找递推式不能每一个都用两重迭代去求

7.1.2 （x1,y1）-（x2,y2）之和

7.2 代码实现

7.2.1 左上角全部

推荐使用方法2：在外围加上一行一列！

#方法1：使用原矩阵！
#输出一个二维矩阵
def output(a):
    n = len(a)
    for i in range(0,n):
        print(" ".join(map(str,a[i][0:])))

def input_list():
    return list(map(int,input().split()))

n,m = input_list()
a = [[0]*(m) for i in range(n)]
sum_ = [[0]*(m) for i in range(n)]

#输入一个二维数组
for i in range(0,n):
    a[i] = input_list()
output(a,n)

for i in range(0,n):
    for j in range(0,m):
        sum_[0][0] = a[0][0]
        if i==0 and j!=0:
            sum_[i][j] = a[i][j]+sum_[i][j-1]
            continue
        if i!=0 and j==0:
            sum_[i][j] = a[i][j]+sum_[i-1][j]
            continue
        sum_[i][j] = sum_[i][j-1]+sum_[i-1][j]+a[i][j]-sum_[i-1][j-1]
output(sum_,n)

#方法2 在外围扩充一行一列0
def output(a):
    n = len(a)
    for i in range(1,n):
        print(" ".join(map(str,a[i][1:])))


def input_list():
    return list(map(int,input().split()))

n,m = input_list()
a=[[0]*(m+1) for i in range(n+1)]
sum_ = [[0]*(m+1) for i in range(n+1)]
for i in range(1,n+1):
    a[i] = [0]+input_list()
for i in range(1,n+1):
    for j in range(1,m+1):
        sum_[i][j] = sum_[i][j-1]+sum_[i-1][j] +a[i][j] -sum_[i-1][j-1]
output(a)
output(sum_)

#例题

7.2.2 任意子矩阵

#方法2 在外围扩充一行一列0
def output(a):
    n = len(a)
    for i in range(1,n):
        print(" ".join(map(str,a[i][1:])))


def input_list():
    return list(map(int,input().split()))

n,m = input_list()
a=[[0]*(m+1) for i in range(n+1)]
sum_ = [[0]*(m+1) for i in range(n+1)]
for i in range(1,n+1):
    a[i] = [0]+input_list()
for i in range(1,n+1):
    for j in range(1,m+1):
        sum_[i][j] = sum_[i][j-1]+sum_[i-1][j] +a[i][j] -sum_[i-1][j-1]
output(a)
output(sum_)
print(sum_)
#
#任意子矩阵
x1,y1 =input_list()
x2,y2 =input_list()
sum1 = sum_[x2][y2] - sum_[x1-1][y2] - sum_[x2][y1-1] +sum_[x1-1][y1-1]
print(sum1)

7.3 例题

7.3.1 统计子矩阵

def output(a):
    n = len(a)
    for i in range(1,n):
        print(" ".join(map(str,a[i][1:])))


def input_list():
    return list(map(int,input().split()))


def get_a(n,m):
    a = [[0] * (m + 1) for i in range(n + 1)]
    for i in range(1,n+1):
        a[i] = [0]+input_list()
    return a


def get_presum(a,n,m):
    sum_ = [[0]*(m+1) for i in range(n+1)]
    for i in range(1,n+1):
        for j in range(1,m+1):
            sum_[i][j] = sum_[i][j-1]+sum_[i-1][j] +a[i][j] -sum_[i-1][j-1]
    return sum_

#任意子矩阵
def get_sum(sum_,x1,y1,x2,y2):
    sum1 = sum_[x2][y2] - sum_[x1-1][y2] - sum_[x2][y1-1] +sum_[x1-1][y1-1]
    return sum1

#例题1
N,M,K= input_list()
a = get_a(N,M)
sum_ = get_presum(a,N,M)

ans = 0
for x1 in range(1,N+1):
    for y1 in range(1,M+1):
        for x2 in range(x1,N+1):
            for y2 in range(y1,M+1):
                sum1 = get_sum(sum_,x1,y1,x2,y2)
                if sum1<=K:
                    ans +=1
print(ans)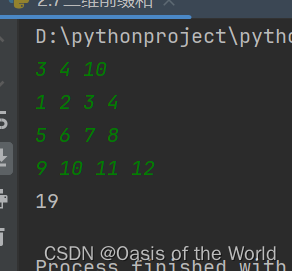

8 差分

8.1 定义

差分数组是任意两个数字求差

很重要的一点是：！！！差分数组的前缀和等于原数组！！！

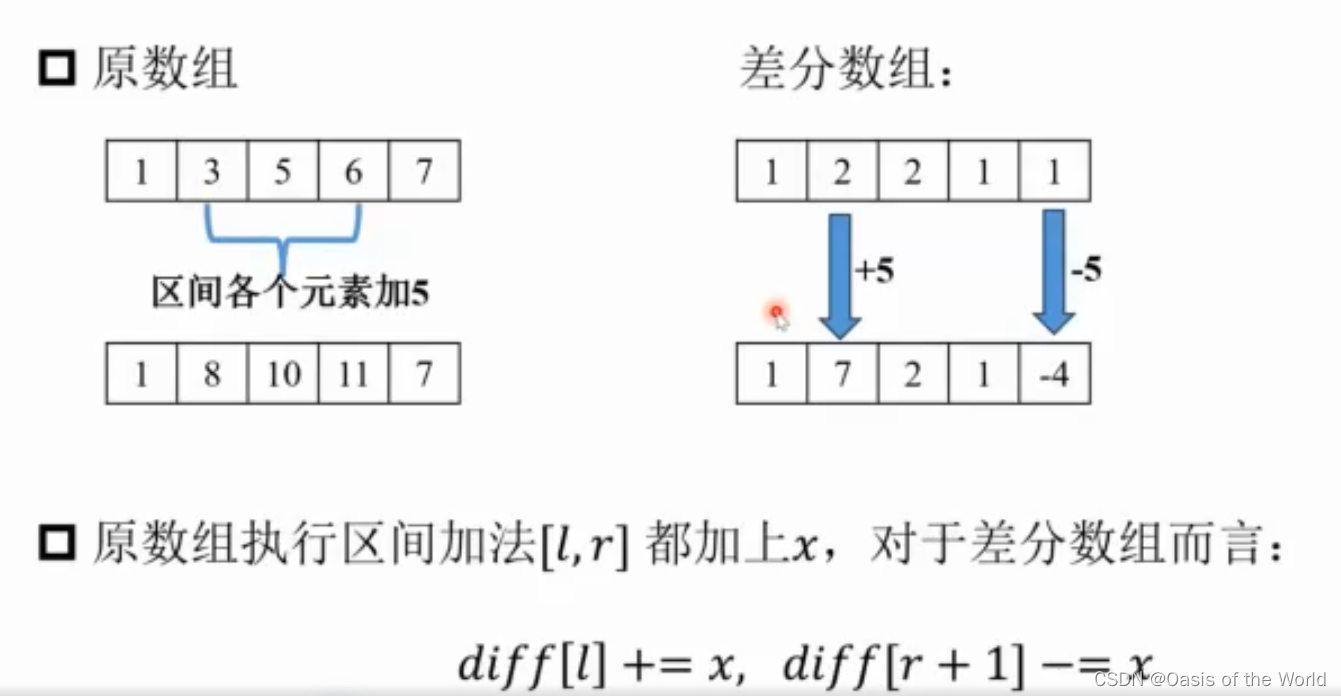
得到差分数组后，将原数组加上差分数组就是最后的结果！

8.2 例子

8.2.1 区间更新

def input_list():
    return list(map(int,input().split()))

#注意这个数组是从1开始的!!!!意味着给定的下标和实际的下标相差1
while True:
    try:
        n,m = input_list()
        # print(n,type(n))
        # print(m)
        a = input_list()
        diff = [0]*(n+1)
        diff[0] = a[0]
        for i in range(1,n):
            diff[i] = a[i] -a[i-1]
        #给定的m个操作
        for j in range(m):
            # print("121312")
            x,y,z = input_list()
            x = x-1
            y = y-1
            diff[x] += z
            diff[y+1] -=z
            a[0] = diff[0]
            for i in range(1,n):
                a[i] = diff[i]+a[i-1]
        print(' '.join(map(str,a)))


    except:
        break

9 二维差分数组

9.1 定义

在（x1,y1）到（x2,y2）这个矩阵里的元素都加上固定的值！哦

用上差分数组降低时间复杂度！

过程：

加上的3会把那一行：3那一个格后面的所有都加上3，所以用-3平衡掉影响！

找到差分数组后将原数组和它进行运算即可！

9.2 代码实现



##二维的
def input_list():
    return list(map(int,input().split()))


def output(a):
    n = len(a)
    for i in range(1,n-1):
        print(" ".join(map(str,a[i][1:m+1])))


n,m = input_list()
a = [[0]*(m+2) for i in range(n+2)]
# output(a)
for i in range(1,n+1):
    a[i] = [0] +input_list() +[0]
diff =[[0]*(m+2) for i in range(n+2)]
# output(a)

for i in range(1,n+1):
    for j in range(1,m+1):
        diff[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] +a[i-1][j-1]
# output(diff)
print("请输入x1,y1:")
x1,y1 = input_list()

print('请输入x2,y2:')
x2,y2 = input_list()
print("请输入需要增加的元素:")
k = int(input())

diff[x1][y1] +=k
diff[x1][y2+1] -=k
diff[x2+1][y1] -=k
diff[x2+1][y2+1] +=k

# output(diff)
for i in range(1,n+1):
    for j in range(1,m+1):
        a[i][j] =diff[i][j]+ a[i - 1][j]+a[i][j - 1]-a[i-1][j-1]

output(a)

10 离散化

10.1 定义（去重排序，返回下标）

10.2 算法步骤

10.3 代码

def Discrete(a):
    #a是输入的列表#return是返回的结果
    b = list(set(a))
    b = sorted(b)
    print(b)
    value = list(range(0,len(b)))
    dic = dict(zip(b,value))

    ans = []
    #对a中的每一个x返回b的下标
    for x in a:
        ans.append(dic[x])
    return ans

a = list(map(int,input().split()))
print(Discrete(a))