CSP-S 真题：格雷码

news2024/9/29 5:37:40

原文链接：CSP-S 真题第二讲：格雷码

说明：CSDN和公众号文章同步发布，需要第一时间收到最新内容，请关注公众号【比特正传】。

一、题目背景

题目来源：CSP-S 2019年 T1

题目考察点：递归、搜索

题目链接：https://www.luogu.com.cn/problem/P5657

二、题目分析

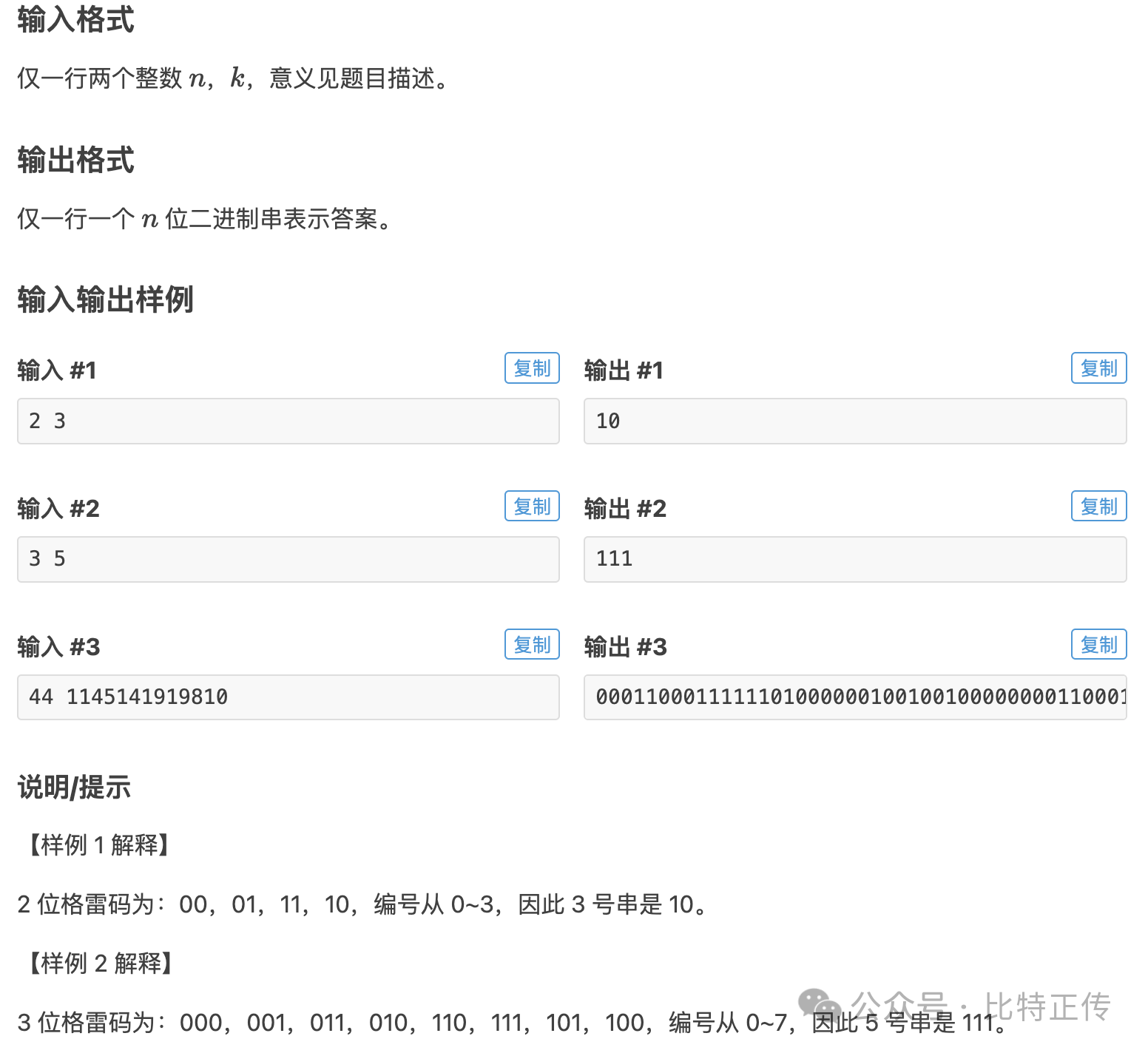
首先，仔细阅读题目，并结合3个样例来深刻理解题意。

思考一下，对于有n位二进制的格雷码，最高位（约定输出结果的左边为高位，右边为低位）应该输出0还是1呢？我们把n位二进制的格雷码一分为二，左半部分有 $2^{n-1}$ 个格雷码，右半部分有 $2^{n-1}$ 个格雷码，可以发现一个规律，左半部分的格雷码的最高位都是0，右半部分的格雷码的最高位都是1，因此当前第n位是0还是1取决于当前的k，如果k在左半部分，那么应该输出0，k在右半部分应该输出1。

根据上面的思路，我们输出完第n位后呢？剩下了n-1位二进制，对于第n-1位呢？是不是又和上面的思路一模一样，因此我们考虑使用递归。

如果将当前n个二进制分为左和右两部分，左边 $2^{n-1}$ 个格雷码，右边 $2^{n-1}$ 个格雷码，那么当 $k< 2^{n-1}$ 时(k从0开始，所以是小于而不是小于等于)，此时输出0，在左半部分继续找第k个，因此递归dfs(n-1, k)，如果 $k\geqslant 2^{n-1}$ ，那么一定在右边，因此先输出1，然后继续递归，此时需要注意了，本来在n位二进制中，是第k个元素，但是现在只能递归右半部分，因此在右半部分中，是第 $k- 2^{n-1}$ 个，还有一点需要注意，在右半部分中，基于n-1位二进制的元素，是倒着遍历，所以对于n-1的二进制，顺着应该是第 $2^{n-1} - (k- 2^{n-1})-1$ , 因为右边总共就 $2^{n-1}$ 个，是逆序的第 $k-2^{n-1}$ 个，那么就是正序的第 $2^{n-1} - (k- 2^{n-1})-1$ 个（不好理解的话，在本子上画一画），因此输出1后，递归dfs(n-1, $2^{n-1} - (k- 2^{n-1})-1$ )。

有了以上的思路，代码就好些了，code如下：

三、AC code

#include "bits/stdc++.h"
using namespace std;
#define ull unsigned long long
ull n, k;
// n表示二进制位数，k表示第k个格雷码
void dfs(ull n, ull k) {
    if(n<1) return;  // 递归结束条件
    ull res = 1;  // 一定要是ull类型的1，否则默认为int的1，会越界
    res = res << n-1; // 等价于2^(n-1)
    if(res > k) { // 在左半部分，因此k从0开始，所以是小于而不是小于等于
        cout << 0;  // 先输出0
        dfs(n-1, k);  // 递归
    } else {
        cout << 1;  // 在右半部分，输出1
        dfs(n-1, res - (k-res) -1);  // 递归，推导见上面的分析
    }
}

int main() {
    cin >> n >> k;
    dfs(n, k);
    return 0;
}