疏雨池塘见
微风襟袖知
目录
归并排序的介绍
基本思想
时间复杂度分析
⭐归并排序步骤
空间复杂度分析
代码展示
✨归并排序的非递归
代码展示
总结🔥

归并排序的介绍
| 归并排序,是创建在归并操作上的一种有效的排序算法。 |
| 算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序(nlogn),为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。 |
基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
| 分解(Divide):将n个元素分成个含n/2个元素的子序列 |
| 解决(Conquer):用合并排序法对两个子序列递归的排序 |
| 合并(Combine):合并两个已排序的子序列已得到排序结果 |
分治展开图
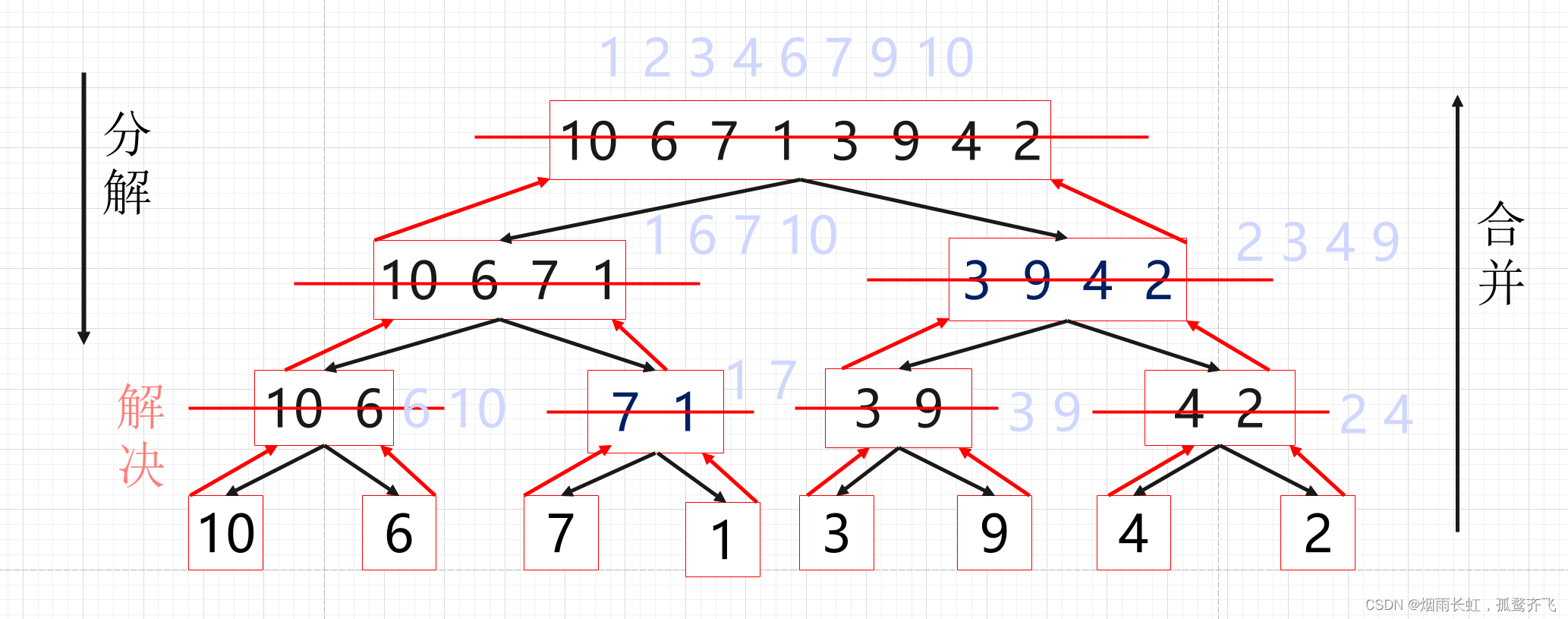
为了好理解我们可以扩展开来:
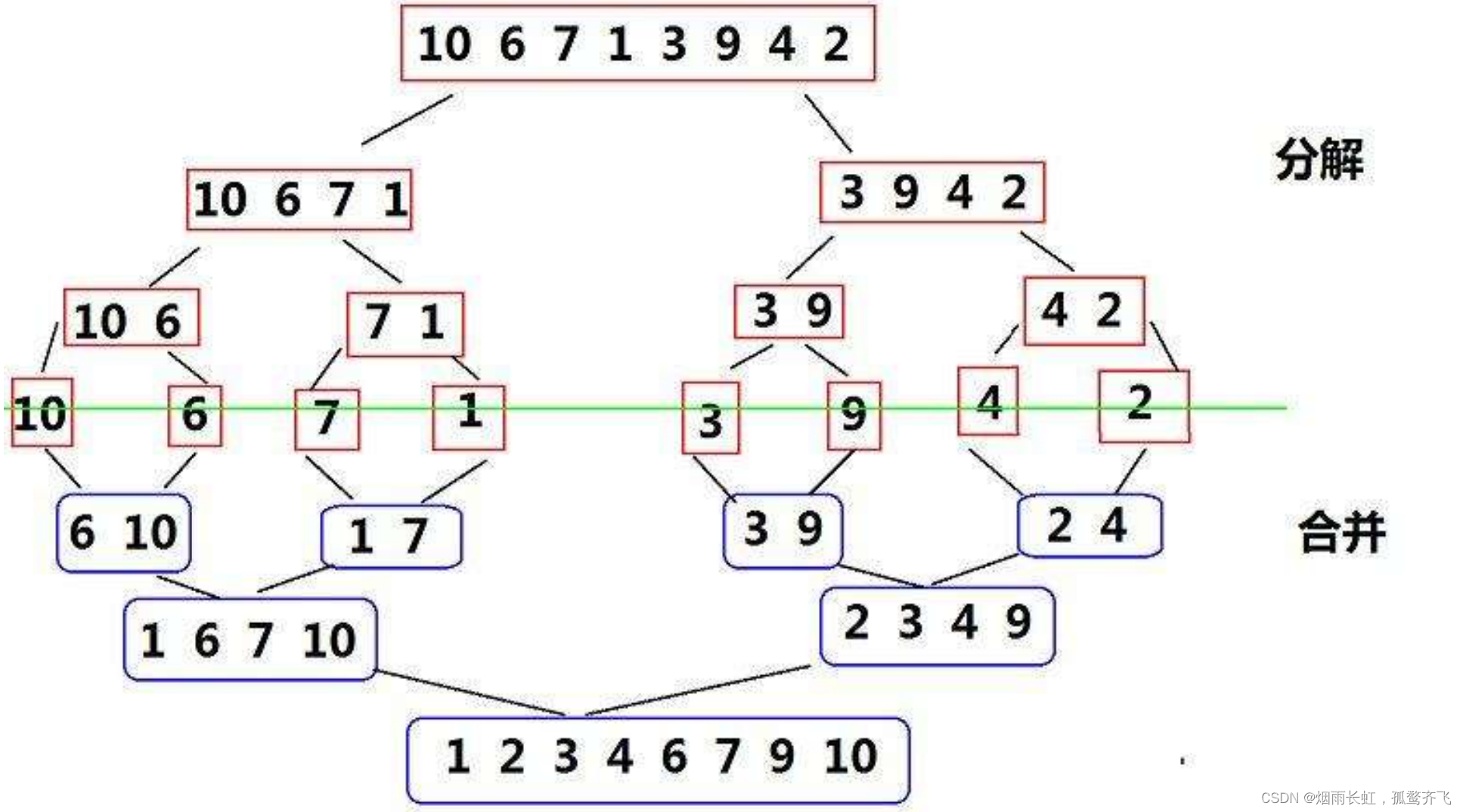
⭐归并图解:
首先把一个序列从中间分割成 2 部分,再把 2 部分分成 4 部分,依次分割下去,直到分割成单个的数据,再把这些数据两两比较归并到一起,使之有序,不停的比较归并,最后成为一个有序的序列。
时间复杂度分析
递归的第一层,将n个数划分为2个子区间,每个子区间的数字个数为n/2; |
递归的第二层,将n个数划分为4个子区间,每个子区间的数字个数为n/4; |
递归的第三层,将n个数划分为8个子区间,每个子区间的数字个数为n/8; |
| ...... |
| ...... |
递归的第logn层,将n个数划分为n个子区间,每个子区间的数字个数为1; |
归并排序的过程中,需要对当前区间进行对半划分,直到区间的长度为1。
也就是说,每一层的子区间,长度都是上一层的1/2。
这也就意味着,当划分到第logn层的时候,子区间的长度就是1了。
而归并排序的操作,则是从最底层开始(子区间为1的层),对相邻的两个子区间进行合并
过程如下:
在第logn层(最底层),每个子区间的长度为1,共n个子区间,每相邻两个子区间进行合并,总共合并n/2次。n个数字都会被遍历一次,所有这一层的总时间复杂度为O(n); |
在第二层,每个子区间长度为n/4,总共有4个子区间,每相邻两个子区间进行合并,总共合并2次。n个数字都会被遍历一次,所以这一层的总时间复杂度为O(n); |
| ...... |
在第一层,每个子区间长度为n/2,总共有2个子区间,只需要合并一次。n个数字都会被遍历一次,所以这一层的总时间复杂度为O(n); |
✨通过上面的过程我们可以发现,对于每一层来说,在合并所有子区间的过程中,
n个元素都会被操作一次,所以每一层的时间复杂度都是O(n)。而之前我们说过,归并排序划分子区间,将子区间划分为只剩1个元素,需要划分logn次。每一层的时间复杂度为O(n),共有logn层,所以归并排序的时间复杂度就是O(nlogn)。
⭐归并排序步骤
我们还是以刚刚的序列为例
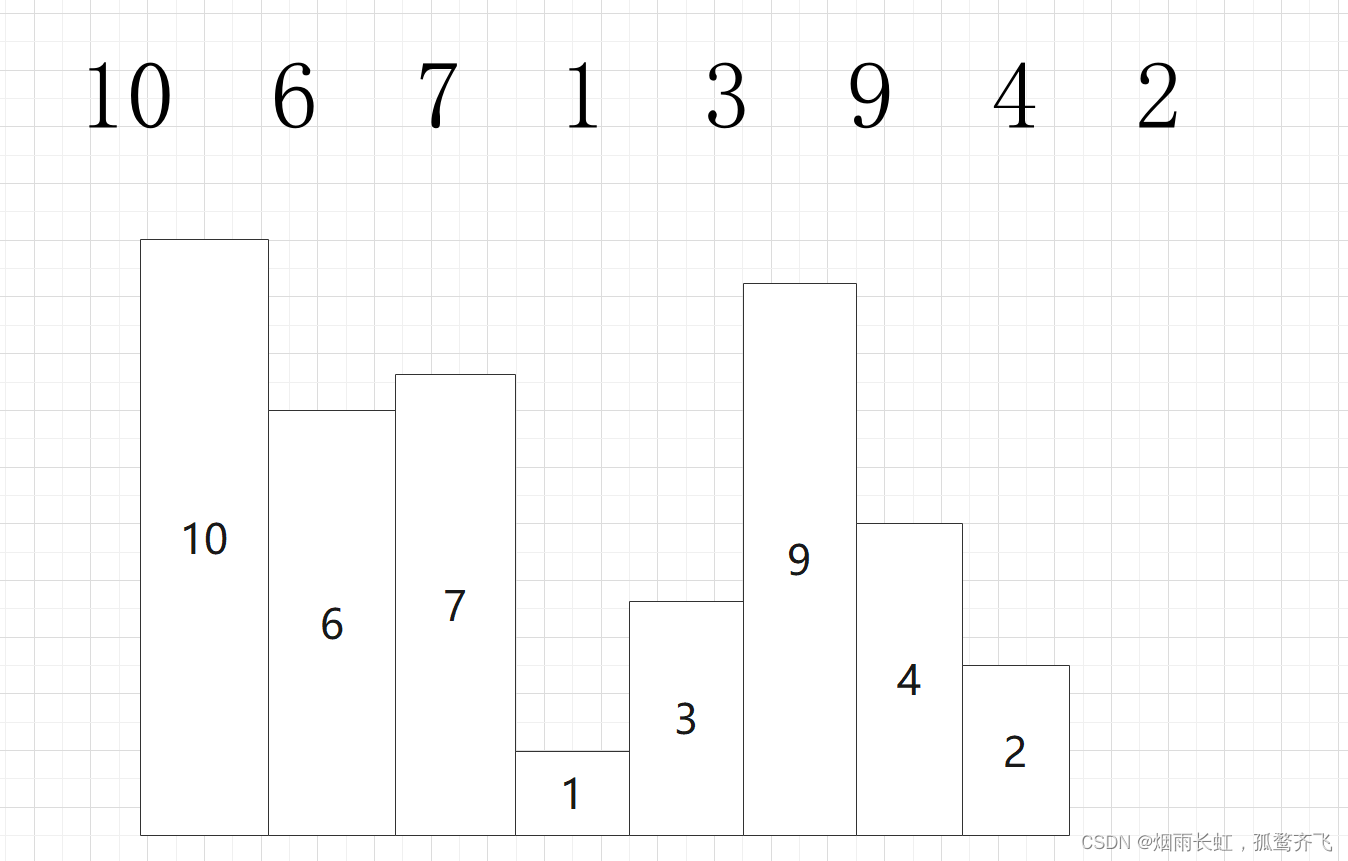
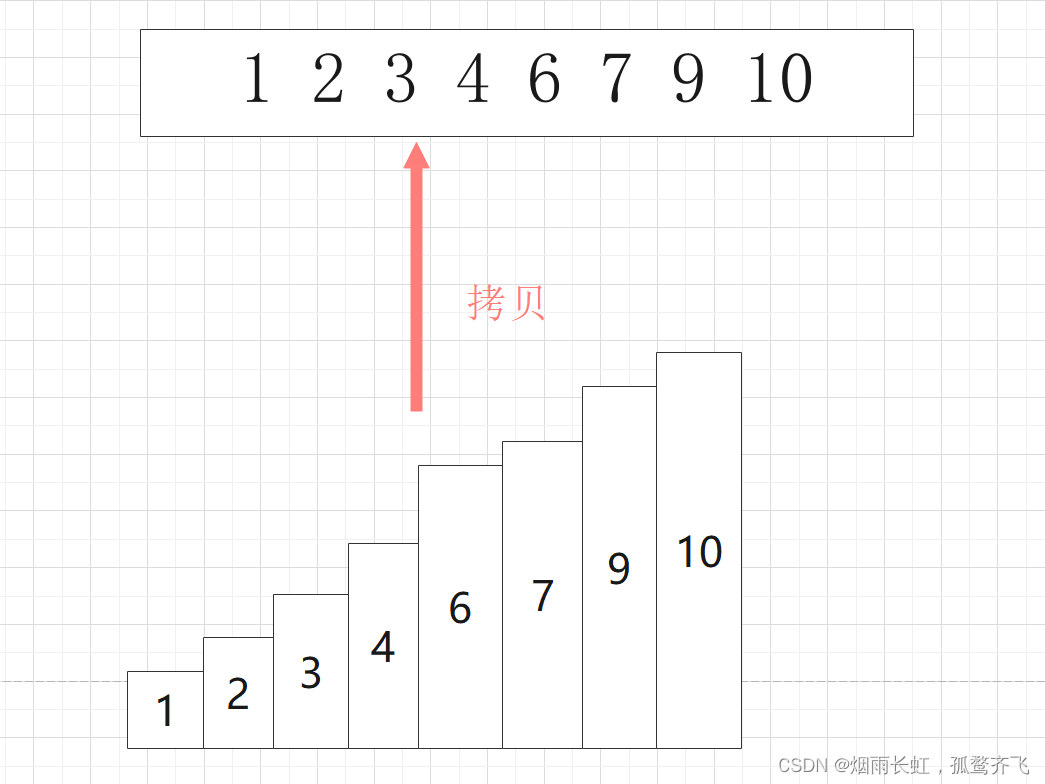
| ⭐我们先将一个序列分成左区间和右区间,在分治成一个单元,通过比较排序后归并成一个有序序列 |
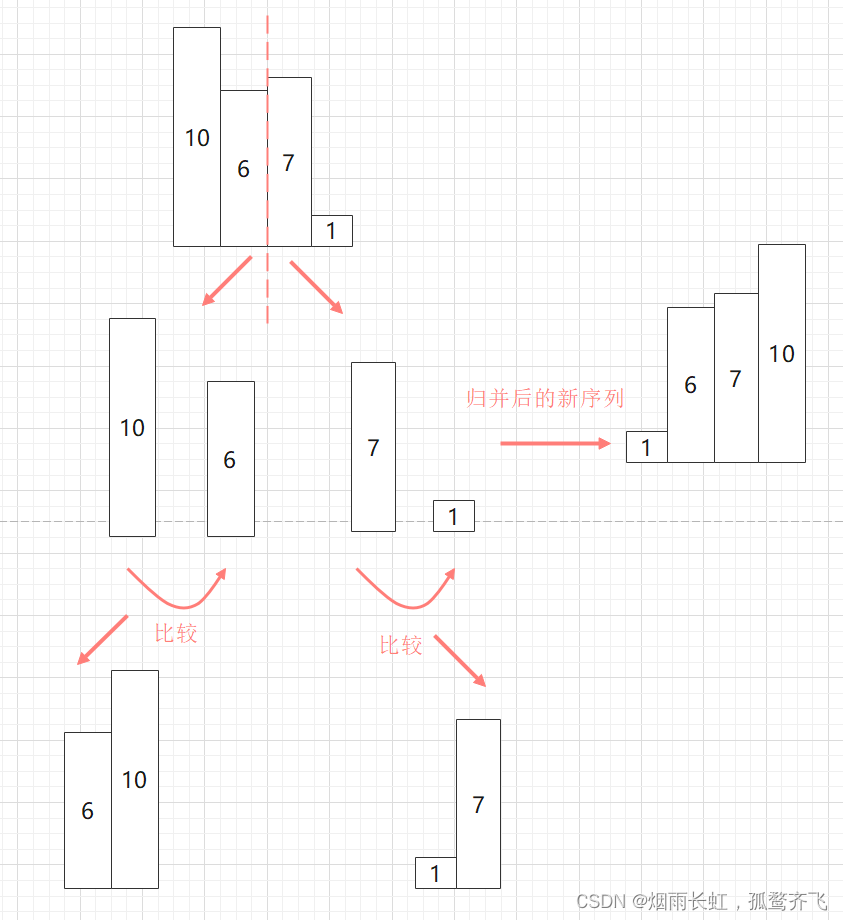
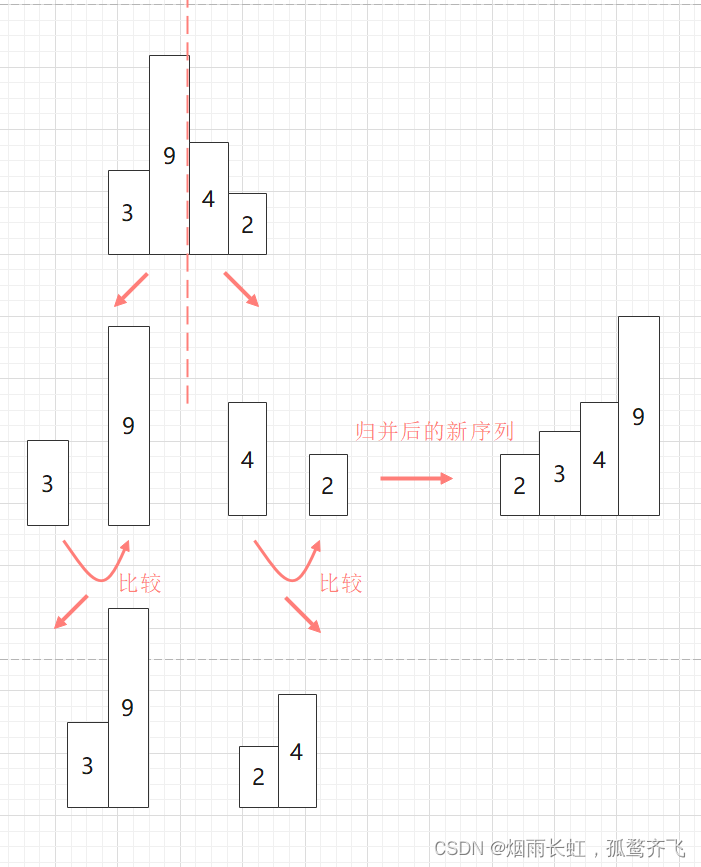
| ⭐然后在定义一个新数组存储左右区间的值,通过连续比较左右的起始值,将较小的尾插到新数组中 |
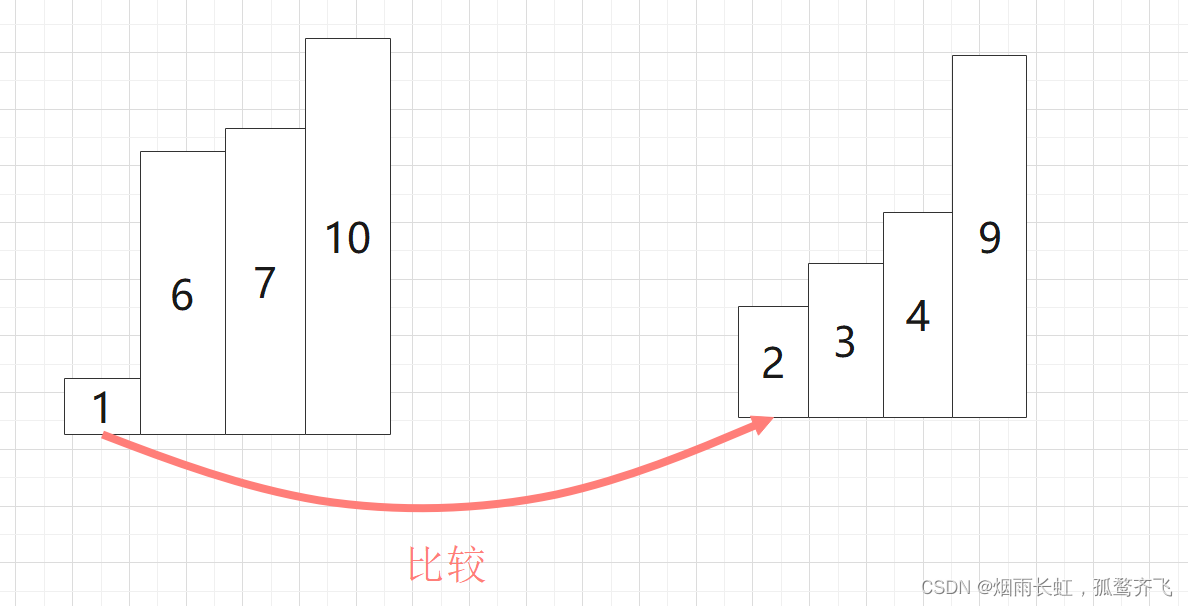

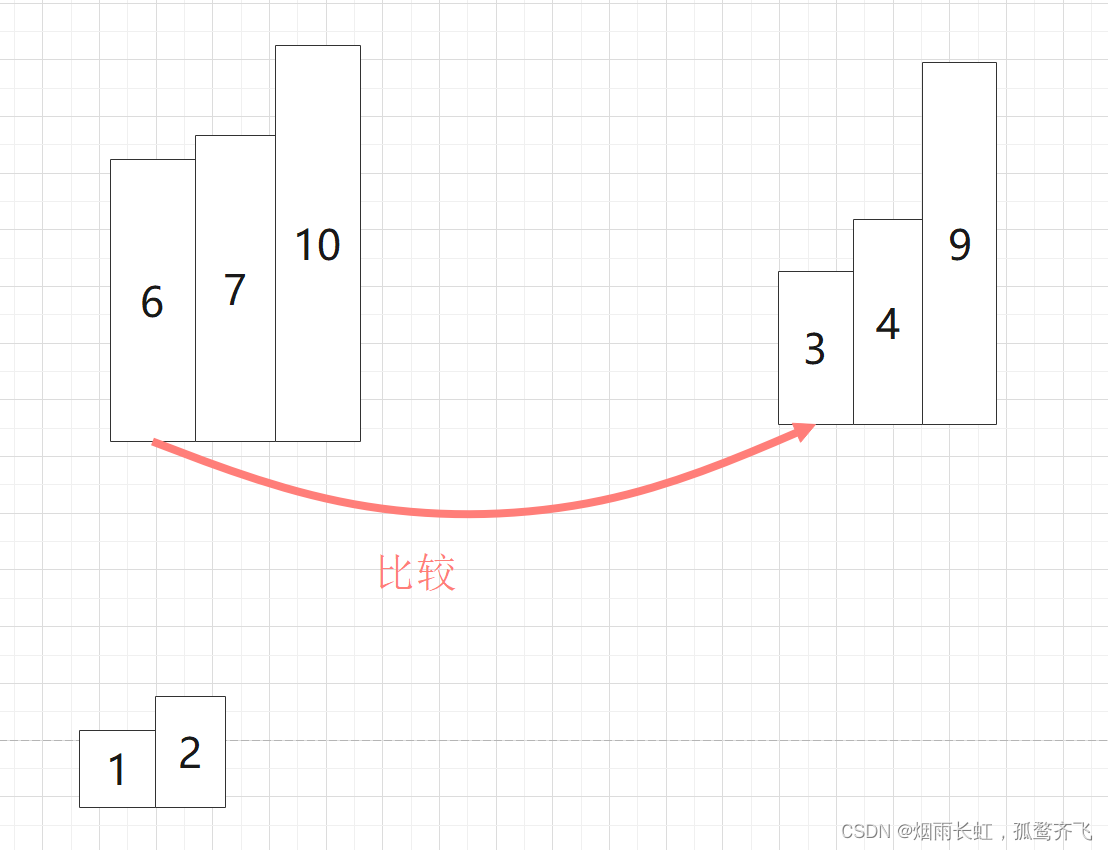
| ⭐最后将排好序的序列拷贝到原序列的空间即可 |
空间复杂度分析
| ✨因为要开辟和原来一样大小的新数组,所以空间复杂度为:O(n) |
代码展示
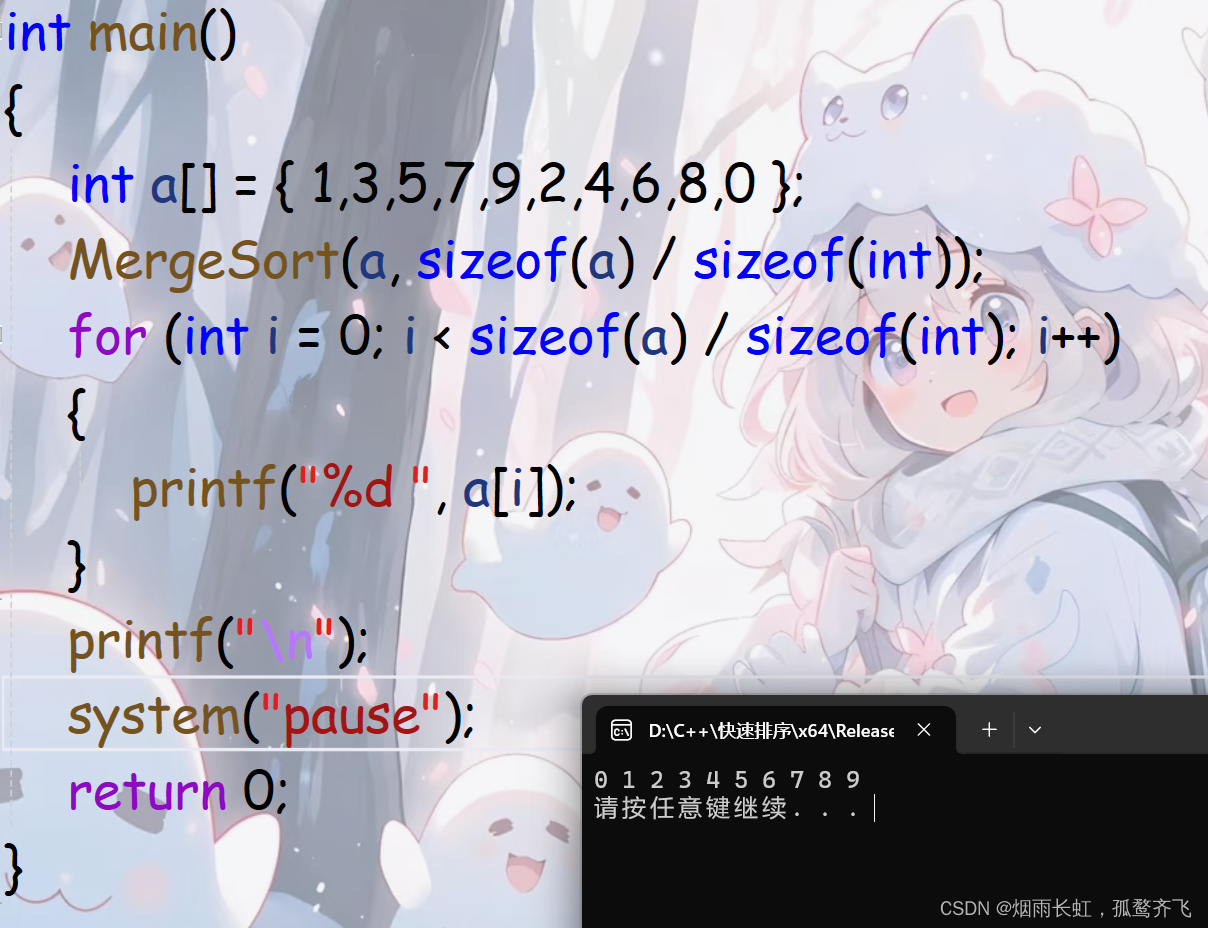
void _MergeSort(int* a, int begin, int end, int* tmp) { //判断递归终止条件,如果end小于等于begin,则表示当前子序列只有一个元素或者为空,无需排序,直接返回 if (begin == end) return; //分成左右序列 int mid = (begin + end) / 2; _MergeSort(a, begin, mid, tmp); _MergeSort(a, mid + 1, end, tmp); int begin1 = begin, end1 = mid; int begin2 = mid+1, end2 = end; int i = begin; //归并 while (begin1 <= end1 && begin2 <= end2) { //数据小的插入新数组 if (a[begin1] <= a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } //若序列为奇数,则最后还有一个单元尾插 //判断最后一个单元的插入 while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } //拷贝序列 memcpy(a + begin, tmp + begin, sizeof(int) * (end-begin+1)); } void MergeSort(int* a, int n) { //开辟新数组的空间 int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc"); exit(-1); } _MergeSort(a, 0, n - 1, tmp); //释放空间 free(tmp); tmp = NULL; }代码测试
✨归并排序的非递归
💞因为递归是一种压栈的操作,而系统提供的栈中的空间并不是很多,所以在数据量庞大项目中我们往往会选择非递归的方法
首先我们定义 gap 为归并每组的数据个数

对大框架:
先来找找规律
| 四个元素需要归并两次 |
| 八个元素需要归并三次 |
| 十六个元素需要归并四次 |
归并循环的次数 k 和数组元素个数 n 的关系是:
所以我们可以这样控制外层循环
int gap = 1;
while (gap < n)
{
... ...
gap *= 2;
}对小框架:
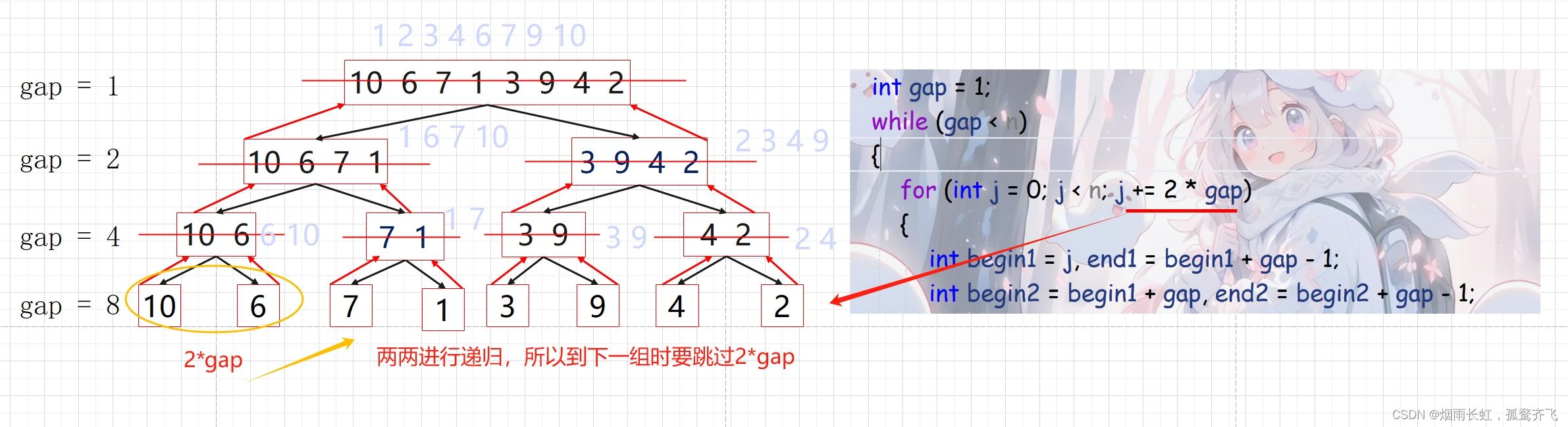
我们根据图中的 gap 来思考
<1>10和10归,6和6归,7和7归,1和1归 ... ...
<2>10和6归,7和1归,3和9归,4和2归
<3>10、6和7、1归,3,9和4,2归
<4>10,6,7,1和3,9,4,2归
从而数组整体有序
gap从1开始,每归并一次便扩大两倍
每次循环的区间可以这样定义:
1 组: [ i , i + gap - 1]
2 组: [ i + gap , i + 2*gap - 1]
... ...
i 控制进行比较轮到的组号,控制进行归并的组号
所以我们可以这样设计内层循环:
for(int i=0;i<n;i+=2*gap)
{
... ...
}🌤️易错点:
| <1>每小组合并完之后再去拷贝 |
| <2>区间合并的起始位置和结束位置的确定 |
| <3>拷贝的长度问题 |
| <4>越界问题 |
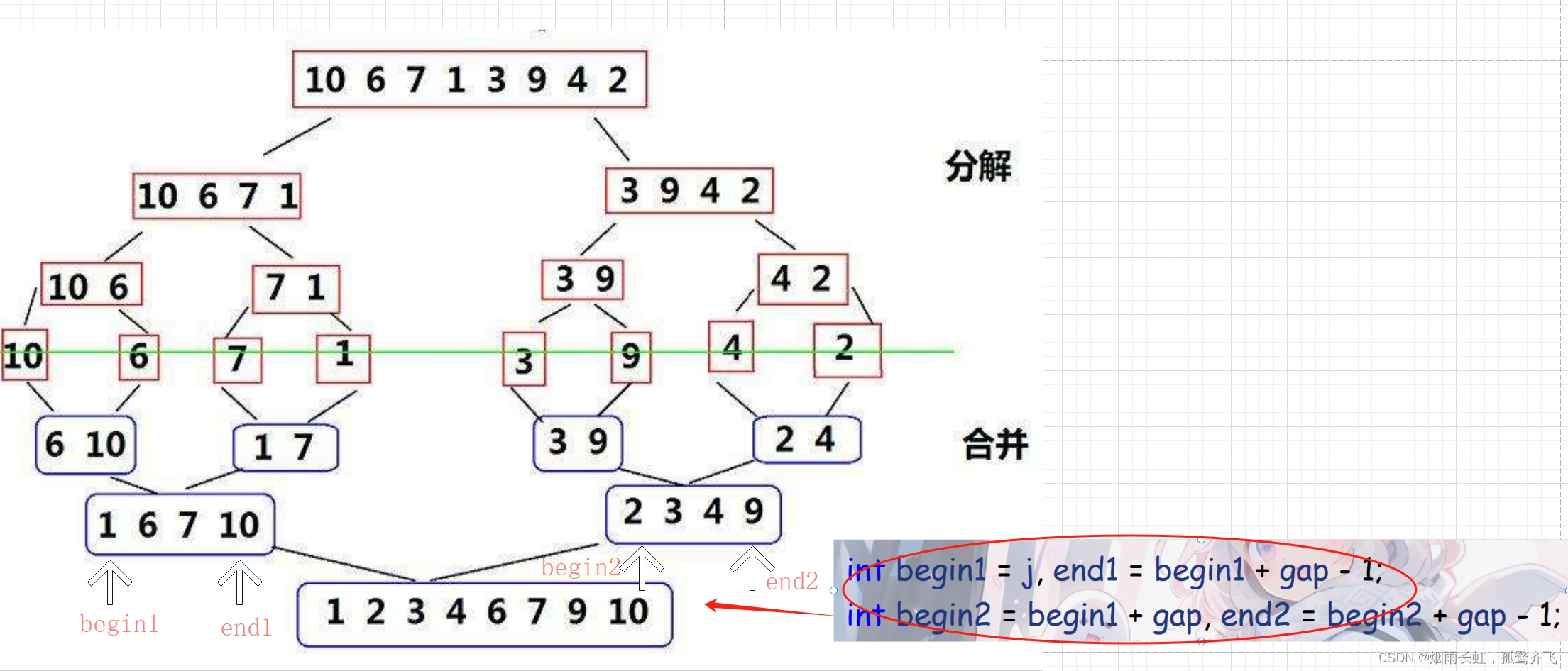
区间合并的起始位置和结束位置的确定
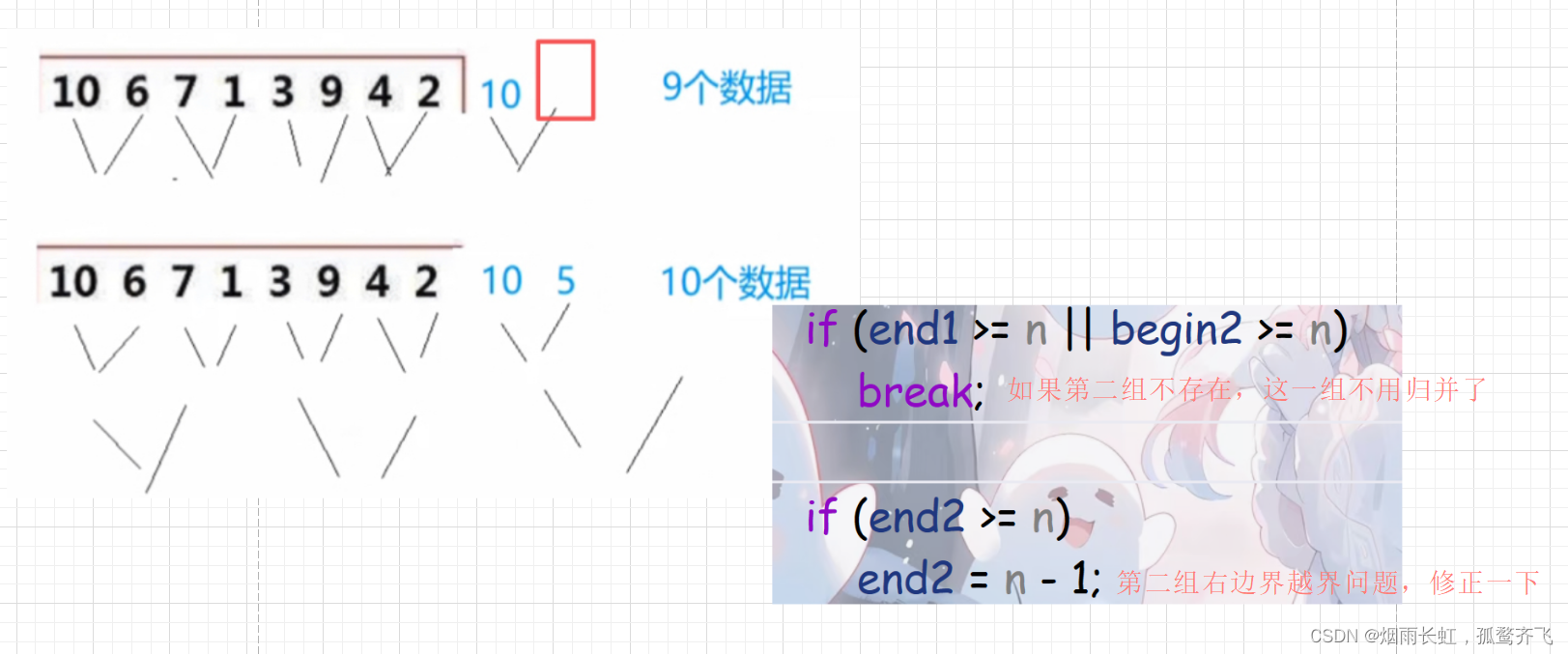
越界问题(合并的组数不一定都是2的次方倍)
代码展示
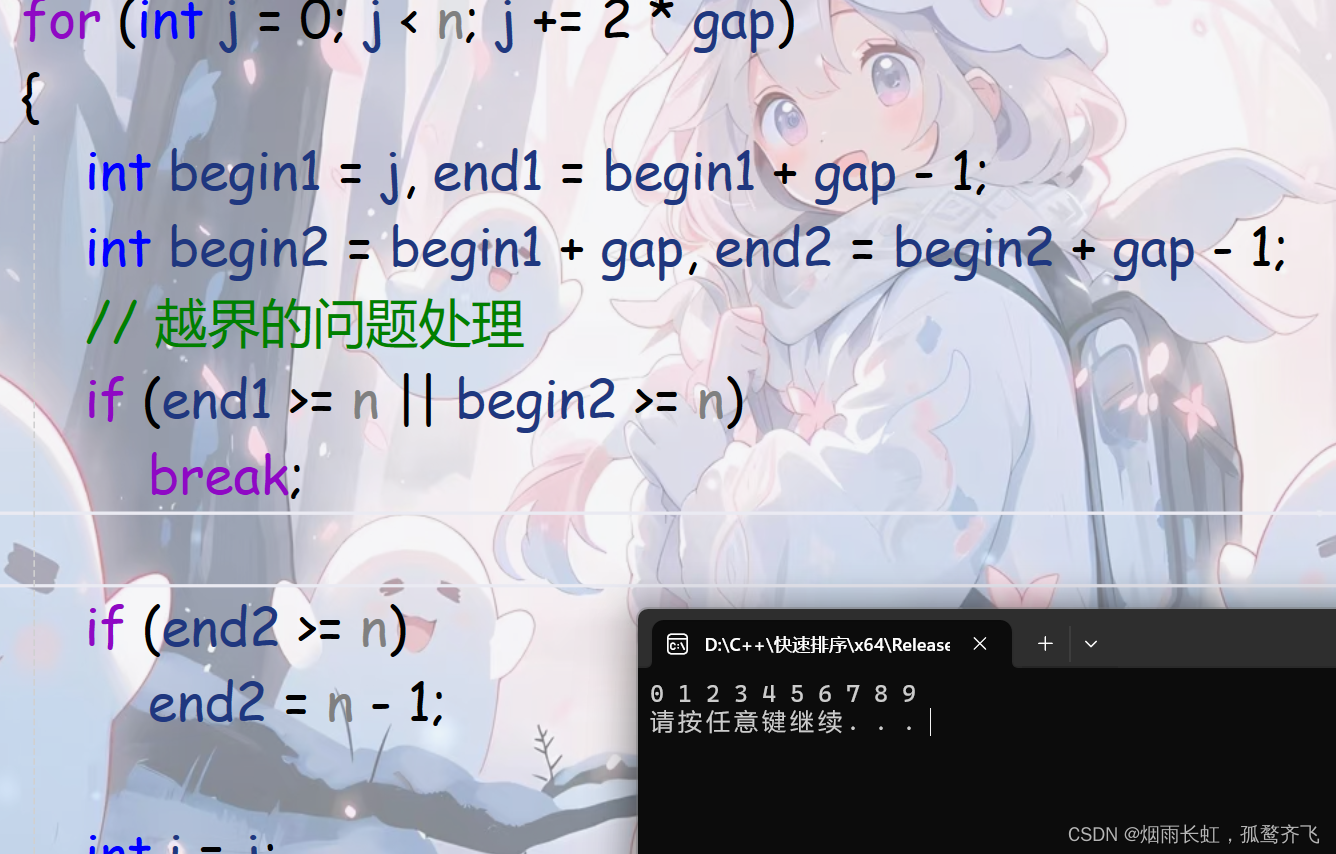
void MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc"); exit(-1); } //gap 归并每组的数据个数 int gap = 1; while (gap < n) { for (int j = 0; j < n; j += 2 * gap) { int begin1 = j, end1 = begin1 + gap - 1; int begin2 = begin1 + gap, end2 = begin2 + gap - 1; // 越界的问题处理 if (end1 >= n || begin2 >= n) break; if (end2 >= n) end2 = n - 1; int i = j; // 依次比较,取小的尾插tmp数组 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] <= a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1)); } gap *= 2; } free(tmp); tmp = NULL; }代码测试
总结🔥
归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题 时间复杂度:O(nlogn) 空间复杂度:O(n) 稳定性:稳定 归并排序适用于各种数据规模的排序,而且对于大规模数据的排序效果较好。它的时间复杂度稳定在O(nlogn),不会因为数据规模的增大而导致时间复杂度的增加。此外,归并排序还适用于外部排序,即对于无法一次性加载到内存的大规模数据进行排序。