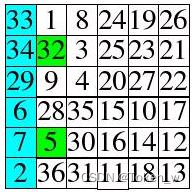
Exercise 14.1-1
呼叫顺序为:
OS−SELECT(T.root,10)
OS−SELECT(T.root.left,10)
OS−SELECT(T.root.left.right,2)
OS−SELECT(T.root.left.right.left,2)
OS−SELECT(T.root.left.right.left.right,1)
然后,我们得到返回的节点(键为20)是T.root.left.right.left.right
Exercise 14.1-2
OS-RANK(T,x)的运算如下:r被设为0,y被设为x。在while循环的第一次迭代时,y被设为键为38的节点。在第二次迭代中,r增加到2,y设置为键为30的节点。在第三次迭代中,y被设置为键为41的节点。在第四次迭代中,r增加到15,y设置为键为26的节点,即根节点。这将打破while循环,并返回第15级。
Exercise 14.1-3
![]()
Exercise 14.1-4
Exercise 14.1-5
期望的结果是OS-SELECT(T,OS-RANK(T,x)+i)。它的运行时间是O(h),根据红黑树的性质,它等于O(lg(n)) 。
Exercise 14.1-6
首先对要插入的节点z执行通常的BST插入过程。然后对从根到z的路径上的每个节点的秩加1,使z在该节点的左子树中。因为添加的节点是叶节点,它没有子树,所以它的秩总是1。当对x执行左旋转时,它在子树中的排名将保持不变。x右的秩会增加x的秩,再加1。如果我们对节点y进行右旋转,它的秩将递减y.left .rank + 1。y.left的等级将保持不变。对于z的删除,从z到根的路径上递减每个节点的秩,使z位于该节点的左子树中。对于任何旋转,使用与之前相同的规则。
Exercise 14.1-7
参见算法INV-COUNT(L)。它确实假设列表中的所有元素都是不同的。为了使它适应不一定不同的情况,每次我们进行搜索时,我们应该选择在无序遍历中首先出现的键的元素。
Exercise 14.1-8
在圆上选择一个点,并给它赋键值1。任何点的秩将是它在从点1开始的序列中读取时的位置,顺时针绕圈读取。接下来,我们用一个键标记每个点。顺时针绕圈阅读,如果一个点的弦伴有一个键,则分配给它相同的键。否则,为其分配下一个最低的未使用整数键值。然后使用问题2-4-d解决方案中给出的算法来计算反转的次数(基于键值),需要注意的是,如果i的同伴的秩小于j的秩,则从键i到键j的反转(i > j)不计算。
Exercise 14.2-1
在无序遍历的所有节点上,添加prev和succ指针。如果我们保持头节点是第一个节点,并且使它循环连接,那么这显然允许四个操作在常数时间内完成。我们仍然需要确保在所有的树修改中维护这个链表结构。假设我们将一个节点插入到BST中作为左子节点,那么我们可以将它插入到这个双链表中,就在它的父节点之前,这可以在常量时间内完成。类似地,如果它是右子元素,那么我们将把它插入它的父元素之后。元素的删除只是链表中常见的删除。
Exercise 14.2-2
由于节点的黑高度仅取决于其子节点的黑高度和颜色,定理14.1意味着我们可以在不影响其他红黑树操作的渐近性能的情况下保持该属性。对于维护节点的深度,情况并非如此。如果我们删除树的根,我们可能不得不更新O(n)个节点的深度,这使得DELETE操作逐渐比以前慢。
Exercise 14.2-3
执行旋转操作后,从被旋转移动的两个节点中较深的一个开始,比如x,设置x.f = x.left.f⊗x.a⊗x.right.f。然后,对旋转中较高的节点做同样的事情。对于大小,设置x.size = x.left t.size + x.right.size + 1,然后在旋转后对更高的节点执行相同的操作。
Exercise 14.2-4
下面的算法运行时间为Θ(m + lgn)。为了找到需要打印的最小和最大的元素,可能会有多达O(lg n)次递归调用,而每一次常数时间调用都会打印a和b之间的m个键中的一个。我们不能做得比这更好,因为有m个键要输出,而找到一个键需要lg n的搜索时间。
Exercise 14.3-1
重新排列节点后,从移动的两个节点中较低的开始,将其Max属性设置为其右端点的最大值,并将其子节点的两个Max属性设置为最大值。对两个移动节点中较高的节点执行相同的操作。
Exercise 14.3-2
将第3行中的弱不等式改为严格不等式。
Exercise 14.3-3
考虑通常给出的区间搜索,但是,我们并没有在有重叠的时候立即跳出循环,我们只是跟踪最近看到的重叠,并继续在循环中运行,直到我们到达T.nil。然后我们返回最近看到的重叠。我们知道这是最小左端点的重叠区间因为搜索总是往左它包含一个重叠区间,而左子结点就是左端点较小的子结点。
Exercise 14.3-4
该算法最多检查每个节点两次,并执行常数时间检查,因此运行时间不会超过O(n)。如果在树的一个分支上进行递归调用,那么该分支必须包含重叠区间,因此运行时间也不能超过O(klgn),因为高度最多为n,输出列表中有k个区间。
Exercise 14.3-5
我们可以修改区间树的插入过程,一旦找到放置给定区间的位置,我们就可以根据右侧端点执行插入过程。然后,要执行INTERVAL-SEARCH-EXACTLY(T,i),首先执行对左侧端点的搜索,然后,基于该节点上对右侧端点的BST执行对右侧端点的搜索,如果遇到具有不同左侧端点的元素,则停止搜索。
Exercise 14.3-6
![]()
将元素存储在红黑树中,其中键值是每个数字本身的值。存储在节点x的辅助属性将是根在x的子树中元素之间的最小间隙,根在x的子树中包含的最大值,根在x的子树中包含的最小值。叶子上的最小间隙为∞。由于我们可以仅使用关于x的键的信息来确定节点x的属性,以及x.left和x.right的属性,定理14.1意味着我们可以在插入和删除期间保持树的所有节点中的值,而不会渐近地影响它们的O(lgn)性能。对于MIN-GAP,只需在常数时间内检查根处的最小间隙。
Exercise 14.3-7
设L是矩形左坐标的集合。设R是矩形右坐标的集合。在O(nlgn)时间内对这两个集合进行排序。然后,我们将有一个指向L的指针和一个指向R的指针。如果指向L的指针更小,则在T上调用区间搜索,查找与左侧对应的上下区间。如果它包含与这个矩形的上下边界相交的点,那么就有一个交集,所以停止。否则,将这个区间加到T上,并将指针增量为L。如果R较小,则去掉右手边对应的上下区间,并将指针增量为R。由于所使用的所有区间树操作在时间O(lg(n))内运行,而我们最多只调用它们3n次,因此我们的运行时间为O(n lg(n))