[USACO1.5] [IOI1994]数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

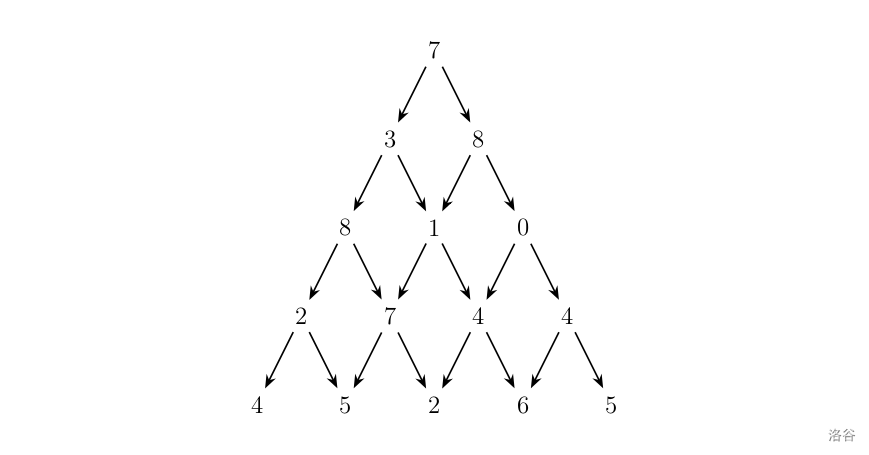
在上面的样例中，从 $7\to 3\to 8\to 7\to 5$ 的路径产生了最大权值。

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

30

提示

【数据范围】
对于 $100\%$ 的数据，$1\le r\le 1000$，所有输入在 $[0,100]$ 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

AC代码：

#include<map>
#include<set>
#include<stack>
#include<cmath>
#include<queue>
#include<string>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<numeric>
#include<iomanip>
#define endl '\n'
using namespace std;

typedef long long ll;
typedef pair<int, int>PII;
const int N=3e5+10;
const int MOD=1e9 + 7;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e6 + 10;

int r;
int dp[1001][1100], a[1010][1010];
int main()
{
    cin >> r;
	for(int i = 1; i <= r; i ++)
	{
		for(int j = 1; j <= i; j ++)
		{
	        cin >> a[i][j];
		}
	}
	for(int i = 0; i <= r; i ++)
	{
		for(int j = 0; j <= i + 1; j ++)
		{
			dp[i][j] = -INF;
		}
	}
	dp[1][1] = a[1][1];
	for(int i = 2; i <= r; i ++)
	{
		for(int j = 1; j <= i; j ++)
		{
			dp[i][j] = max(dp[i - 1][j] + a[i][j], dp[i - 1][j - 1] + a[i][j]);
		}
	}
	int res = -INF;
	for(int i = 1; i <= r; i ++)
	{
		res = max(dp[r][i], res);
	}
	cout << res << endl;
	return 0;
}