1、数据结构三要素?
逻辑结构、物理结构、数据运算
2、数组和链表的区别?
- 数组的特点: 数组是将元素在内存中连续存放,由于每个元素占用内存相同,可以通过下标迅速访问数组中任何元素。数组的插入数据和删除数据效率低,插入数据时,这个位置后面的数据在内存中都要向后移。删除数据时,这个数据后面的数据都要往前移动。但数组的随机读取效率很高。因为数组是连续的,知道每一个数据的内存地址,可以直接找到给地址的数据。如果应用需要快速访问数据,很少或不插入和删除元素,就应该用数组。数组需要预留空间,在使用前要先申请占内存的大小,可能会浪费内存空间。并且数组不利于扩展,数组定义的空间不够时要重新定义数组。
- 链表的特点: 链表中的元素在内存中不是顺序存储的,而是通过存在元素中的指针联系到一起。比如:上一个元素有个指针指到下一个元素,以此类推,直到最后一个元素。如果要访问链表中一个元素,需要从第一个元素开始,一直找到需要的元素位置。但是增加和删除一个元素对于链表数据结构就非常简单了,只要修改元素中的指针就可以了。如果应用需要经常插入和删除元素你就需要用链表数据结构了。不指定大小,扩展方便。链表大小不用定义,数据随意增删。
- 数组的优点:随机访问性强;查找速度快。
- 数组的缺点: 插入和删除效率低;可能浪费内存;内存空间要求高,必须有足够的连续内存空间;数组大小固定,不能动态拓展。
- 链表的优点: 插入删除速度快;内存利用率高,不会浪费内存;大小没有固定,拓展很灵活。
- 链表的缺点: 不能随机查找,必须从第一个开始遍历,查找效率低。
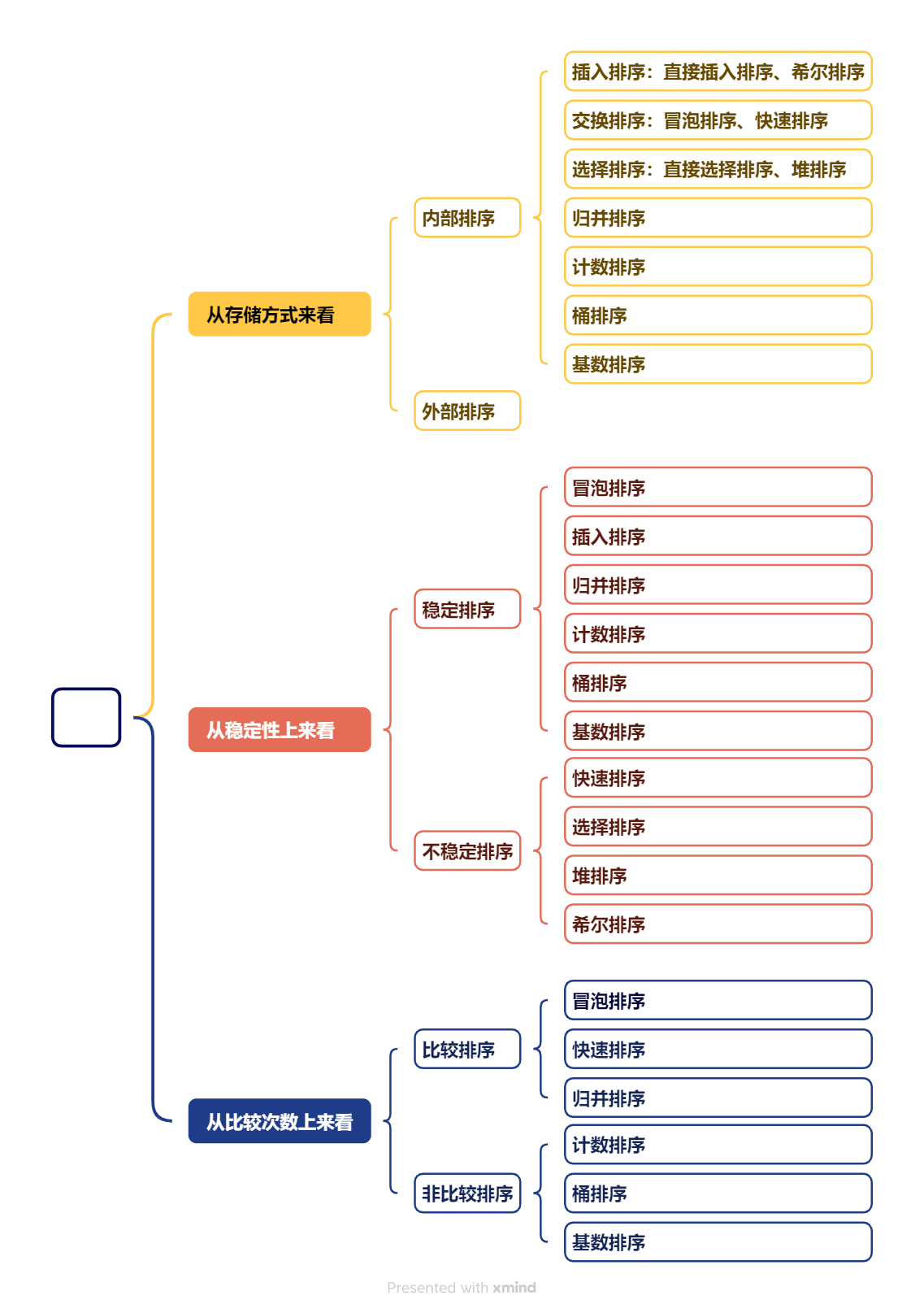
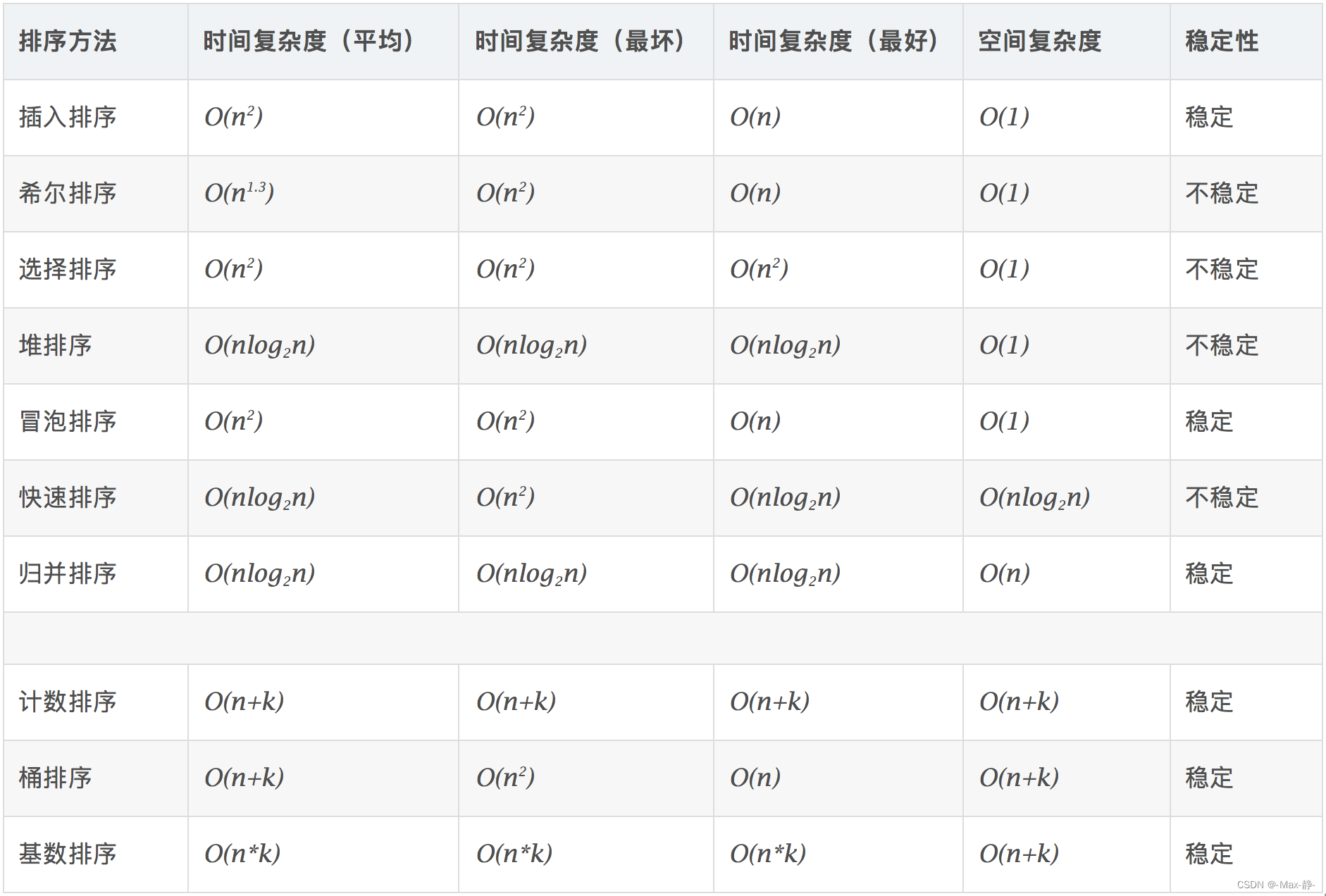
3、排序有哪些分类?
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序
4、冒泡排序(Bubble Sort)
算法步骤:
- 从第一个元素开始,比较相邻的两个元素。如果前一个元素比后一个元素大(如果是升序排序的话),则交换它们的位置。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
5、插入排序(Insertion Sort)
算法步骤:
- 从第一个元素开始,该元素可以认为已经被排序。
- 取出下一个元素,在已经排序的元素序列中从后向前扫描。
- 如果该元素(已排序)大于新元素,将该元素移到下一位置。
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤2~5,直到所有元素均排序完毕。
6、希尔排序(Shell Sort)
算法步骤:
- 选择增量序列:首先,需要选择一个增量序列t1,t2,…,tk,其中ti > tj, tk = 1。这个序列的选择对希尔排序的性能至关重要。常用的增量序列有Hibbard增量序列、Sedgewick增量序列等。
- 分组与预排序:按照当前的增量ti,将待排序序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。此时,整个序列是“基本有序”的。
- 逐步缩小增量并重复排序:每排序完一次子序列(即增量为ti的一趟排序)后,更新增量为ti-1,并重复步骤2,进行下一趟排序,直到增量减小到1。此时,整个序列已经基本有序,可以对整个序列进行一次直接插入排序,得到最终排序结果。
7、选择排序(Selection Sort)
算法步骤:
- 遍历待排序序列,设立一个指针,初始指向序列的第一个元素。
- 从当前指针位置开始,依次与后面的元素比较,找到最小(或最大)的元素,并记录其位置。
- 将找到的最小(或最大)元素与当前指针位置的元素进行交换。
- 将指针向后移动一位,重复步骤2和步骤3,直到指针移动到序列的倒数第二个元素。
- 此时,最后一个元素已经是序列中的最大(或最小)元素,排序完成。
8、快速排序(Quick Sort)
算法步骤:
- 从序列中选取一个元素作为基准(pivot)。
- 将序列中小于基准的元素放在基准的左边,大于基准的元素放在基准的右边。这个操作称为分区(partition)操作,完成后基准元素处于序列的中间位置。此时,该基准元素在排序后的最终位置已经确定。
- 递归地对基准左边和右边的两个子序列进行快速排序。
9、归并排序(Merge Sort)
算法步骤:
- 分解:将待排序的序列划分为若干个长度为1的子序列,每个子序列自然有序。
- 递归进行归并:递归地将相邻的子序列两两归并,得到若干个有序的较长子序列,直到最终合并为一个完整的有序序列。
10、堆排序(Heap Sort)
算法步骤:
- 建堆:将无序序列构造成一个大顶堆(或小顶堆)。此时,整个序列的最大值(或最小值)就是堆顶的根节点。
- 堆调整:将堆顶元素与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个序列重新构造成一个堆,这样会得到n个元素中的次大值。如此反复执行,便能得到一个有序序列了。
11、计数排序(Counting Sort)
首先,扫描待排序数组,确定数组的最大值和最小值;
然后,建立一个与最大值和最小值范围相对应的计数数组,并统计每个元素出现的次数;
最后,根据计数数组的信息,将待排序数组中的元素放到正确的位置上。
12、桶排序(Bucket Sort)
- 确定桶的数量和大小:首先,需要确定桶的数量以及每个桶的大小范围。桶的数量可以基于待排序数组的长度和数据分布来决定。每个桶的大小范围则是根据数据的最大值和最小值来划分的。
- 分配数据到桶中:遍历待排序数组,根据每个元素的值将其放入对应的桶中。这个过程需要根据桶的大小范围来判定每个元素应该放入哪个桶。
- 桶内排序:对每个桶内的元素进行排序。这里可以使用其他排序算法,如插入排序、归并排序或快速排序等,对桶内的元素进行进一步的排序。
- 合并桶中的数据:最后,按照桶的顺序,将桶内的元素依次合并起来,形成最终的排序结果。
13、基数排序(Radix Sort)
- 确定最大位数:首先,需要找到待排序数组中的最大值,确定其位数。这将决定需要进行多少轮排序。
- 从最低位开始排序:基数排序从最低位(个位)开始,对数组进行排序。在每一轮排序中,可以使用稳定的排序算法(如计数排序或桶排序)对相应位上的数字进行排序。
- 逐渐向高位排序:完成最低位的排序后,继续向更高位(十位、百位等)进行排序。每一轮排序都会根据当前位的数字值对数组进行重排。
- 合并排序结果:经过多轮排序后,数组中的元素将按照从最低位到最高位的顺序排列。由于每一轮排序都是稳定的,所以最终得到的数组将是一个有序数组。
14、数组和链表的区别?
从逻辑结构上来看,数组必须实现定于固定的长度,不能适应数据动态增减的情况,即数组的大小一旦定义就不能改变。当数据增加是,可能超过原先定义的元素的个数;当数据减少时,造成内存浪费;链表动态进行存储分配,可以适应数据动态地增减的情况,且可以方便地插入、删除数据项。
从内存存储的角度看;数组从栈中分配空间(用new则在堆上创建),对程序员方便快速,但是自由度小;链表从堆中分配空间,自由度大但是申请管理比较麻烦。
从访问方式类看,数组在内存中是连续的存储,因此可以利用下标索引进行访问;链表是链式存储结构,在访问元素时候只能够通过线性方式由前到后顺序的访问,所以访问效率比数组要低。
15、线性表的存储结构?
16、头指针和头节点?
17、栈(stack)和队列(queue)的区别?
18、什么是二叉树?平衡二叉树?
19、如何唯一确定一棵二叉树?
中序 + 先序/后序/层序
20、图的存储方式有哪些?每一种方式优缺点
21、树的存储结构?
22、图的遍历和树的遍历方式都是什么?
23、图的遍历与树的遍历有什么区别?
24、关键路径和关键活动是什么?
25、什么叫平衡二叉树?
26、什么叫搜索二叉树?
27、什么叫红黑树?
28、数据结构的4种逻辑结构各有什么特点?
(1)集合结构:结构中的数据元素之间除了同属于一种类型外,无其他关系。
(2)线性结构:结构中的数据元素之间存在一对一的关系。
(3)树形结构:结构中的数据元素之间存在一对多的关系。
(4)图状结构或网状结构:结构中的数据元素之间存在多对多的关系。
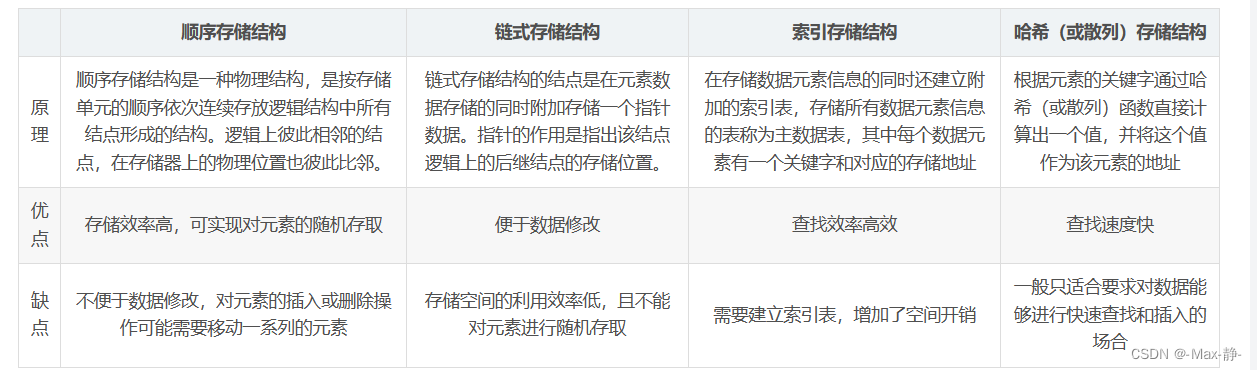
29、数据结构中的存储结构有哪几种?各有什么有优缺点?
30、什么是数据结构?C语言、数据结构、算法以及程序之间的关系是什么?
数据结构是指所有数据元素以及数据元素之间的关系,可以看作是相互之间存在着某种特定关系的集合,因此可以我们将数据结构看成是带结构的数据元素的集合。此外,在通常情况下,选择合适的数据结构可以带来提高运行效率或者存储效率。
数据结构、算法以及程序之间的关系是:数据结构 + 算法 = 程序。
算法不一定要求能够在计算机上直接运行,但程序必须要求能在计算机中运行。C语言只是对算法或者数据结构的描述,描述数据结构和算法不局限于C语言,也可以是C++语言和其他的计算机语言甚至也可以用人的自然语言。
31、常见数据结构?
数组 ;栈;队列;链表;图;树;前缀树;哈希
32、解决哈希冲突的方法
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。
1) 线性探测法
2) 平方探测法
3) 伪随机序列法
4) 拉链法
33、什么是KMP算法?
在一个字符串中查找是否包含目标的匹配字符串。其主要思想是每趟比较过程让子串先后滑动一个合适的位置。当发生不匹配的情况时,不是右移一位,而是移动(当前匹配的长度– 当前匹配子串的部分匹配值)位。
34、什么是B树?
根据B类树的特点,构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些,而且B类树是平衡树,每个结点到叶子结点的高度都是相同,这也保证了每个查询是稳定的。
B树和B+树的区别,以一个m阶树为例。
- 关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
- 存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
- 分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
- 查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。
感谢博主:
感谢博主:https://xgqngu.blog.csdn.net/article/details/112134686
感谢博主:数据结构常见面试题,一网打尽!_数据结构面试题-CSDN博客
感谢博主:数据结构面试题(史上最全基础面试题,精心整理100家互联网企业面经) - 知乎
感谢博主:数据结构面试常见问题总结-CSDN博客