(以 IntelliJ IDEA为例)
1.进入激活网址
https://jetbra.in/s
2.选择一个没有安全警告提示的网址进入

3.下载激活文件并解压(建议放在与IntelliJ IDEA同级目录下)


4.进入IDEA/bin下修改配置文件 ,添加下述三行(注意文件路径修改为自己的)并保存

# 将C:/Program Files/JetBrains/jetbra“”修改为自己环境的ja-netfilter.jar文件所在绝对路径
-javaagent:C:/Program Files/JetBrains/jetbra/ja-netfilter.jar=jetbrains
--add-opens=java.base/jdk.internal.org.objectweb.asm=ALL-UNNAMED
--add-opens=java.base/jdk.internal.org.objectweb.asm.tree=ALL-UNNAMED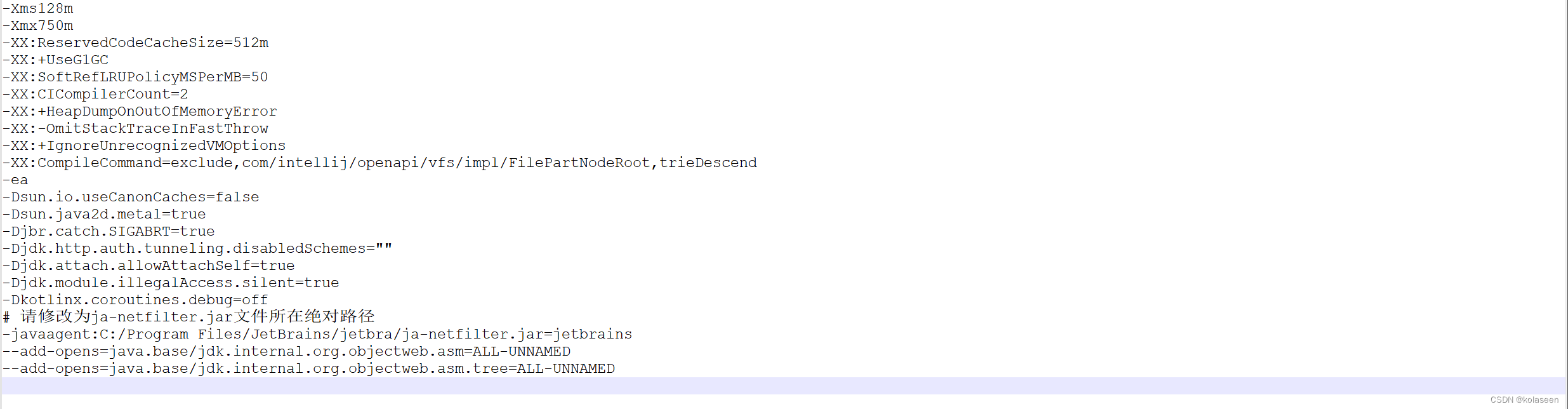
5.在激活网站复制对应激活码

6.进入IDEA使用激活码激活