HyperLogLog

概述

概述。
HyperLogLog并不是一种新的数据结构(实际类型为字符串类型),而是一种基数算法，通过HyperLogLog可以利用极小的内存空间完成独立总数的统计，数据集可以是IP、Email、ID等
如果你负责开发维护一个大型的网站，有一天产品经理要网站每个网页每天的UV(独立用户访问数, Unique Visitor)数据，你会如何实现?
如果统计PV(页面访问量,即Page View)那非常好办，给每个网页一个独立的Redis计数器就可以了，这个计数器的key后缀加上当天的日期，这样来一个请求，incrby一次，最终就可以统计出所有的PV数据。但是UV不一样，它要去重，同一个用户一天之内的多次访问请求只能计数一次。这就要求每一个网页请求都需要带上用户的ID，无论是登录用户还是未登录用户都需要一个唯一的ID来标识。一个简单的方案，那就是为每一个页面一个独立的set集合来存储所有当天访问过此页面的用户ID。当一个请求过来时，我们使用SADD将用户ID塞进去就可以了。通过SCARD可以去除这个集合的大小，这个数字就是这个页面的UV数据。但是，如果页面访问量非常大，比如一个爆款页面几千万的UV，你需要一个很大的set集合来统计，这就非常浪费空间。如果这样的页面很多，那所需要的存储空间是惊人的。为这样一个去重功能就耗费这样多的存储空间，不是很值得，其实需要的数据又不需要太精确，1050w和1060w这两个数字对于老板来说
并没有多大区别，所以我们可以有更好的解决方案。这就是HyperLogLog的用武之地，Redis提供了HyperLogLog数据结构就是用来解决这种统计问题的。HyperLogLog提供不精确的去重计数方案，虽然不精确到那时也不是非常不精确。Redis给出的标准误差是0.81%，这样的精确度已经可以满足上面的UV统计需求了

操作命令

HyperLogLog提供了3个命令:pfadd、pfcount、pfmerge.
例如0815的访问用户是u1、u2、u3、u4, 08-16的访问用户是u4、u5、u6、u7

1.pfadd

pfadd key element [elment …]
pfadd用户向HyperLogLog添加元素，如果添加成功返回1

127.0.0.1:6379> pfadd 08-15:u:id "u1" "u2" "u3" "u4"
(integer) 1

2.pfcount

pfcount key [key …]
pfcount用于计算一个或多个HyperLogLog的独立总数，例如08-15:u:id的独立总数为4

127.0.0.1:6379> pfcount 08-15:u:id
(integer) 4

如果此时向其中插入u1、u2、u3、u90，结果会是5

127.0.0.1:6379> pfadd 08-15:u:id "u1" "u2" "u3" "u90"
(integer) 1
127.0.0.1:6379> pfcount 08-15:u:id
(integer) 5

如果继续往里面插入苏剧，比如插入100万条用户记录。内存增加非常少，但是pfcount的统计结果会出现误差。以使用集合类型和HyperLogLog统计百万级用户访问次数的占用空间对比:(见图所示)可以看到，HyperLogLog内存占用量小的惊人，但是用如此小空间来估算如此巨大的数据，必然不是100%的正确，其中一定存在误差率。0.81%的误差率

3.pfmerge

pfmerge destkey sourcekey [sourcekey …]
pfmerge可以求出多个HyperLogLog的并集并赋值给destkey

3.原理概述

数据原理

HyperLogLog基于概率论中伯努利试验并结合了极大似然估算方法，并作了分桶优化。实际上目前还没有发现更好的在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用概率算法是一个不错的解决方案。概率算法不直接存储数据集合本身，通过一定的概率统计
方法预估值，这种方法可以大大节省内存，同时保证误差控制在一定范围内。目前用于基数基数的概率算法包括:

• Linear Counting(LC):早期的基数估计算法，LC在空间复杂度方面并不算优秀
• LogLog Counting(LLC):LogLog Counting相比LC更加节省内存，空间复杂度更低
• HyperLogLog Counting(HLL): HyperLogLog Counting是基于LLC的优化和改进，在同样空间复杂度情况下，能够比LLC的基数估计误差更小。

例子

• 举个例子，用户A和用户B抛硬币，规则是用户B负责抛硬币，每次抛的硬币可能正面，可能反面。每当抛到正面为一回合，用户B可以自己决定进行几个回合。最后需要告诉用户A最长的那个回合抛了多少次以后出现了正面，再由用户A来猜用户B一共进行了几个回合.
  如图所示，进行了n次，
  第一次:抛了3次才出现正面，此时k=3, n = 1
  第二次:抛了2次才出现正面，此时k=2, n = 2
  第三次:抛了4次才出现正面，此时k=4, n = 3
  …
  第n次试验:抛了7次才出现正面，此时我们估算，k = 7, n = n
  k是每回合抛到1(硬币的正面)所用的次数，，我们已知的是最大的k值，可以用k_max表示。由于每次抛硬币的结果只有0和1两种情况,因此，能够推测出k_max在任意回合出现的概率，并由kmax结合极大似然估计的方法推测出n的次数n=2^(k_max).概率学把这种问题叫做伯努利实验。现在用户B已经完成了n个回合，并且告诉用户A最长的一次抛了4次，用户A此时
  胸有成竹，马上根据公式得出的结果是16，然后用户B却只抛了3次。所以这种预估方法存在较大误差,为了改善误差情况，HLL中引入了发呢同平均的概念。
  

• 同样举抛硬币的例子，如果只有一组抛硬币实验，显然根据公式推导得到的实验次数的估计误差较大，如果100个组同时进行抛硬币实验，样本数变大，受运气影响的概率就很低了，每组分别进行多次抛硬币实验，并上报各自实验过程中抛到正面的抛掷次数的最大值，就能根据100组的平均值预估整体的实验次数了。分桶平均的基本原理是将统计数据划分为m个桶，每个桶分别统计各自的k_max,并能得到各自的基数预估值，最终对这些基数预估值求平均得到整体的基数预估值。LLC中使用几何平均数预估
  整体的基数值，但是当统计数据量较小时误差较大:HLL在LLC基础上做了改进，采用调和平均数过滤掉不健康的统计值。

• 什么是调和平均数呢?
  举个例子。求平均工资:A的是1000/月，B的是30000/月。采用平均数的方式就是(1000+30000)/2=15500
  采用调和平均数的方式就是2/(1/1000 + 1/30000)约等于1935.484.
  可见调和平均数比平均数的好处就是不容易受到大的数据的影响，比平均数的效果是要好的。

结合实例理解实现原理,以统计网页每天的UV数据为例。

1.转为比特串。

通过哈希函数，将数据转为比特串，例如输入5，便转为101，字符串也是一样，这样转化的原因在于要和抛硬币对应上，比特串中0代表了反面，1代表了正面，如果一个数据最终被转换了10010000
那么从右往左，从低位往高位看，可以认为，首次出现1的时候，就是正面.那么基于上面的估算结论，我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验，同样也就可以根据
存入数据中转化后出现1的最大的位置k_max来估算存入了多少数据.

2.分桶。

分桶就是分多少轮。抽象到计算机存储中去，存储的是一个长度为L的位(bit)大数组S,将S平均分为m组，这个m组就是对应多少轮，然后每组所占用的比特个数是平均的，设为P,容易得出下面的关系:

L = S.length
L = m * p
以K为单位，S所占用的内存 = L/8/1024

3.对应。

假设访问用户id为，idn, n->0,1,2,3…
在这个统计问题中，不同的用户id表示了一个用户，那么我们可以把用户的id作为被hash的输入。即:hash(id)=比特串,不同用户的id，拥有不同的比特串。每一个比特串，也必然会至少出现一次1的位置。我们类比每一个比特串为一次伯努利实验。现在要分轮，也就是分桶。所以我们可以设定，每个比特串的前多少位转为10进制后，其值就对应于所在桶的标号。假设比特串的低两位用来计算桶下标志。总共有4个桶，此时有一个用户的id的比特串是:1001011000011.它的所在桶下标位12^1 +12^0=3，处于第三个桶中，即第3轮中。
上面的例子中，计算出桶号后，剩下的比特串是:10010110000,从低位到高位看，第一次出现1的位置是5。也就是说，此时第3个桶中，k_max=5,5对应的二进制是101，将101存入第3个桶。模仿上面的流程，多个不同的用户id，就被粉散到不同的桶中去了，且每个桶有其k_max.然后当要统计出某个页面有多少用户点击量的时候，就是一次估算，最终结合所有桶中的k_max带入估算公式，便能得出估算值

Redis中的HyperLogLog实现

Redis的实现中，HyperLogLog占据12KB(占用内存为16384 * 6 / 8 /1024 = 12K)的大小，共设有16384个桶，即:2^14=16384，每个桶有6位，每个桶可以表达的最大数字是 2^5 + 2^4 + …+ 2^0=63，二进制为:111 111。

对于命令:pfadd key value

在存入时，value会被hash成64位，即64bit的比特字符串，前14位用来分桶，剩下50位用来记录第一个1出现的
位置。之所以选14位，来表达桶编号是因为分了16384个桶，而2^14=16384,刚好地，最大的时候可以把桶利用完，不造成浪费。假设一个字符串的前14位时:00 0000 0000 0010(从右往左看),其十进制值为2.那么value对应转化后的值放到编号为2的桶。

index的转化规则:

首先因为完整的value比特串是64位形式，减去14后，剩下50位，假设极端情况，出现1的位置，是在第50位，即位置是50。此时，index=50.此时先将index转为2进制，它是110010.因为16384个桶中，每个桶是6bit组成的。于是110010就被设置到了第2号桶中去了，50已经是最坏的情况，且它都被容纳进去了。那么其他的不用想也肯定能被容纳进去。因为pfadd的key可以设置多个value.如下

pfadd lgh golang
pfadd lgh python
pfadd lgh java

根据上面的做法，不同的value会被设置到不同桶中去，如果出现了在同一个桶的，即前14位值是一样的，但是后面出现1的位置不一样。那么比较原来的index是否比新index大。是，则替换，否则不变最终地，一个key所对应的16384个桶都设置了很多的value了，每个桶有一个k_max。此时调用pfcount时，按照调和平均数进行估算，同时加以偏差修正，便可以计算出key的设置了多少次value，也就是统计值，具体的估算公式如下:

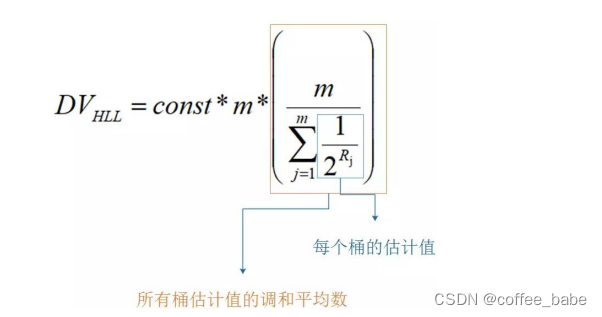
value被转换为64位的比特串，最终被按照上面的做法记录到每个桶中去。64位转十进制就是2^64,HyperLogLog仅仅用了16384 *6/8/1024=12K
存储空间久能统计多达2^64个数，同时在具体的算法实现上，HLL还有一个分阶段偏差修正算法