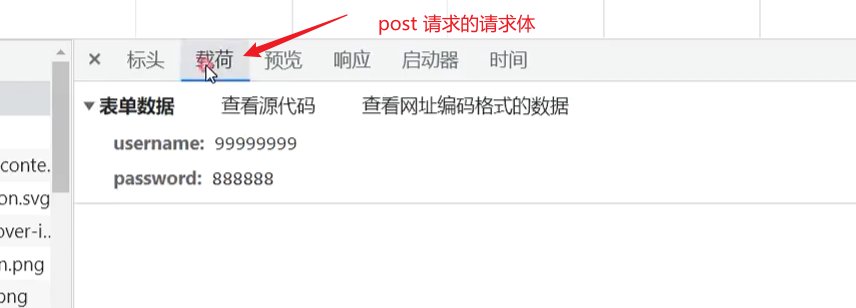
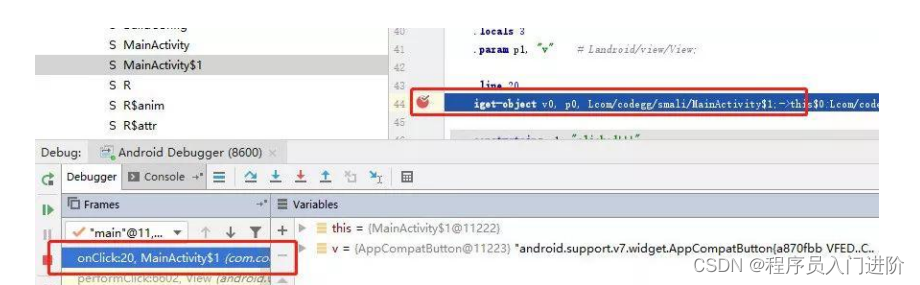
我们在研究数据的二进制表示时遇到这样一个问题:
由于计算中的CPU只有加法器,没有减法器,所以在计算机采用原码做减法时对于:1 - 1 = 0 相当于1 + (-1),用二进制表示为:0001+1001=1001。而1001是二进制的 -1。这明显是不对的,但是计算机又是出入处理的呢?
计算机在处理减法的时候,引入了补码这一概念。许多人接触补码,仅是被告知是“正数不变,负数取反加一”,而对于为什么需要这么做,以及补码本身的存在意义并不清楚。而网上关于补码的解释比较散,故在此写一篇文章记录,希望其他人少走弯路。这篇文章的目的,则是从补码被发明的缘由说起,从根源上:
1)彻底梳理补码形成的过程,说明补码需要解决的问题
2)归纳补码的实质
3)解释补码用于数学运算的正确性
4)解释求补码(负数除符号位以外,按位取反加一)这一操作的可靠性
5)推导补码加减法的运算公式
一、摈弃错误观念
如果你对补码有以下误解,请从现在起忘记这些错误观点的存在:
1)补码是让正数变负数,负数变正数
2)补码是原码数与模互补的数
除了上面的错误观点以外,下面还有几点需要提醒,以免先入为主:
1)不要把补码与“对模求补”的操作直接关联,只需要把补码看成一种全新构造的二进制编码,不需要过度关注补字
2)补码的最高位是符号位,但它不是无依据地定义的,后面会解释补码最高位可以代表正负的原因
一、补码的形成
在计算机的硬件结构中,实现加法器比实现减法器简单的多。人们希望的是构造出一套 “用加法代替减法” 的运算逻辑,构造的结果也就是现在我们所使用的“补码”。
最初的探索
缘起于日常生活的现象,时钟的顺拨与倒拨均可以达到同一钟点。十二小时制中,分针由8点拨到6点,有两种方式:
1)逆时针拨2小时:8-2=6时
2)顺时针拨10小时:8+10=6时
第二种方式本来应该为18时,但由于时钟是十二小时制计时,产生了溢出,显示的是18-12=6时。而这种形式,则是用加法代替了第一种形式的减法,这正是我们想要的,于是对于“以加代减”的逻辑,有了最初的构造:
时钟超出显示上限,则只显示余下的钟点,这恰好是模数加法运算的体现:在模12的情况下(或者说对12取余),以下式子是等价的:
(8−2)mod12=(8+10)mod12=6
按照这个思路,我们在模范围内,也许可以将“X-Y”的减法变更为“X+Y的补数”的加法。
注:所谓m的补数就是:(模-m)的值,如2的补数是12-2=10
二、模数加法的局限
模数加法代替减法是一个很好的思路,但它并不是完美的。上面提及到的情况,事实上只是 “大减小” 的情况,如果出现 “小减大” 情况就出现矛盾了:
举个例子:
在模100的情况下,套用上面的模数加法公式企图代替减法:
(10−30)mod100=−20
( 10 + ( 100 − 30 ) ) mod100 = 80
这和说好的不一样啊,80显然不等于-20,而且也没有因为超越模数而引起取余运算。然而先贤们并不打算前功尽弃……
三、负数的表示法
他们为了继续使用模数加法代替减法,他们做了一个大胆而又粗暴的定义:让80等于-20,即用80代表-20
根据这个规律,推广到一般的情况就是:
负数的表示方式就是它绝对值的补数——规则①
这样做有两个好处:
1)消除了“小减大”情况下的歧义,使得该情况也可用模数加法代替减法。
2)此定义同样可以解释“大减小”的情况,因为它同样吻合 将“X-Y”的减法变更为“X+Y的补数” 的说法(视 -Y 作负数,则它的表示为Y的补数)。
这样做后,无论是“大减小”或是“小减大”,模数加法代替减法都已可适用,可以说已经形成了一套较为通用的以加代减体系。
该负数表示法的结果与缺点
但是注意到,像80这样的大数,失去了自己的意义,在模100的情况下,无法再表示80了。更一般地,因为我们希望正负数尽量成对出现,而且打算用正数表示负数,这意味着在模100的非负数之间,需要划分一半正数用于表示负数,结合规则①的负数表示方式,最终满足这一系列条件的结果是:
在模100条件下:0 ~ 49表示正数本身; 50 ~ 99表示各自补数的负值(如98代表-2)
更一般地:模n情况下,0 ~ n/2 -1表示本身,n/2 ~ n-1表示各自补数的负值——规则②
四、补码的实质
所谓补码,其实只是:非负数和规则①表示的负数,在二进制形式下的表示
所以虽然补码叫补码,但事实上它的本质和补字没有直接关联,它只是一种为了实现模数加法代替减法而构造出来的数字映射罢了。
补码并非在二进制中才有用,根据上面的定义,无论任何进制都不会改变补码体系的准确性。二进制与其它进制,影响只是求补码的简便方式(下面会提及)
补码最高位为符号位的解释
 补码在二进制中的最高位为符号位,其实是因为规则②中,把半模以上的数用作表示负数,而恰好半模以上的数,在二进制表示中的最高位就是1,半模以下最高位是0。
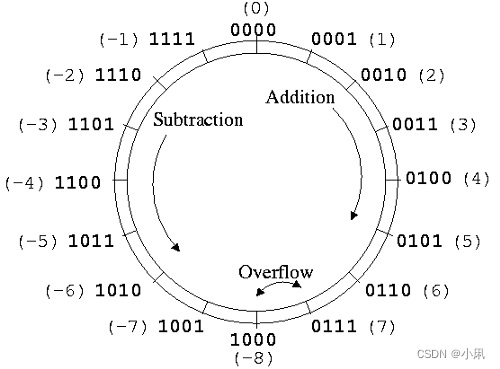
 因此,从数字映射来讲,半模以上的正数确实被规则①映射为了负数;但是单论二进制数字而言,最高位的1仅代表它是半模以上的数,脱离了规则①它与正负符号没有任何关系。
 总之,尽管在补码中,最高位确实可以简单地看做正负标志,但是需要注意的是,这种做法事实上有迹可循,千万不要想当然地以为这只是一种毫无根据的硬性规定
五、原码到负数补码的转换
按位取反加一
上面基本讲解了补码的意义与本质,现在剩下的问题就是在二进制中:原码负数如何求补码?
我们总不能按规则①,依靠十进制定义来求负数表示,再转换成二进制吧?
我们希望的是找到一种原码直接转换成补码的形式
也就是我们喜闻乐见的“除符号位以外,按位取反加一”