引子：

对于一个命题，如何判定命题公式为永真式、永假式和可满足的呢或二个命题公式等价。我们学过二种方法： 1，真值表法：对于变元的所有真值指 派，看对应命题公式的真值。2，命题演算方法：化简命题公式至最简式，看是否存在和     （Ｐ∨¬Ｐ）、（Ｐ∧¬Ｐ）等价，若不则为可满足的，那今天我就来介绍范式方法

定义：什么是范式？

把命题公式化归为一种标准的形式，称此标准形式为范式。

范式分为析取范式和合取范式，设命题变元为：Ｐ、Ｑ、Ｒ，则：（Ｐ∨Ｑ∨Ｒ）的析取式称为“和”；（Ｐ∧Ｑ∧Ｒ）的合取式称为“积”。

什么是基本积与基本和？

命题公式的变元和变元的否定之积称为基本积，而变元和变元的否定之和称为基本和。“基本和”或“基本积”中的子公式”，称为此基本积（和）的因子。

定理：一个基本积必定是永假式，一个“基本和”必定为永真式

AS：Ｐ∧¬Ｐ必为永假式，Ｐv¬Ｐ必定为永真式；

什么是（主）析取范式，极小项概念：？

与给定命题公式等价的一个公式，如果是由基本积之和组成，则称它为命题公式的析取范式

对给定的命题公式来讲，仅含有极小项的析取的等价式称为给定命题公式的主析取范式。

极小项概念：在ｎ个变元的基本积中，若每个变元及其否定并不同时存在，且二者之一出现一次且仅出现一次，则称此基本积为极小项

注意：在真值表中，一个公式的真值为Ｔ的指派所对应的极小项的析取，即为此公式的主析取范式。

方法：1，真值表法  （注意有三个以上的变元，不建议使用）  2 ，等价公式法

AS:求 ¬(Ｐ∧Q)的主析取范式

解：

什么是（主）合取范式  极大项概念？

与给定命题公式等价的一个公式，如果它是由基本和之积所组成，则称它是给定命题公式的合取范式。

在真值表中，一个公式的真值为F的指派所对应的极大项的合取，即为此公式的主合取范式

极大项概念：在ｎ个变元的基本和中，若每个变元与其否定，并不同时存在，且二者之一出现一次且仅出现一次，则称这种基本和为极大项

方法：1，真值表法 （注意有三个以上的变元，不建议使用）   2 ，等价公式法

AS: 求Q∧(Ｐv¬Q)的主合取范式

解：

方法一：

方法二：

看，其实不难！

极大项编码与极小项编码；图解

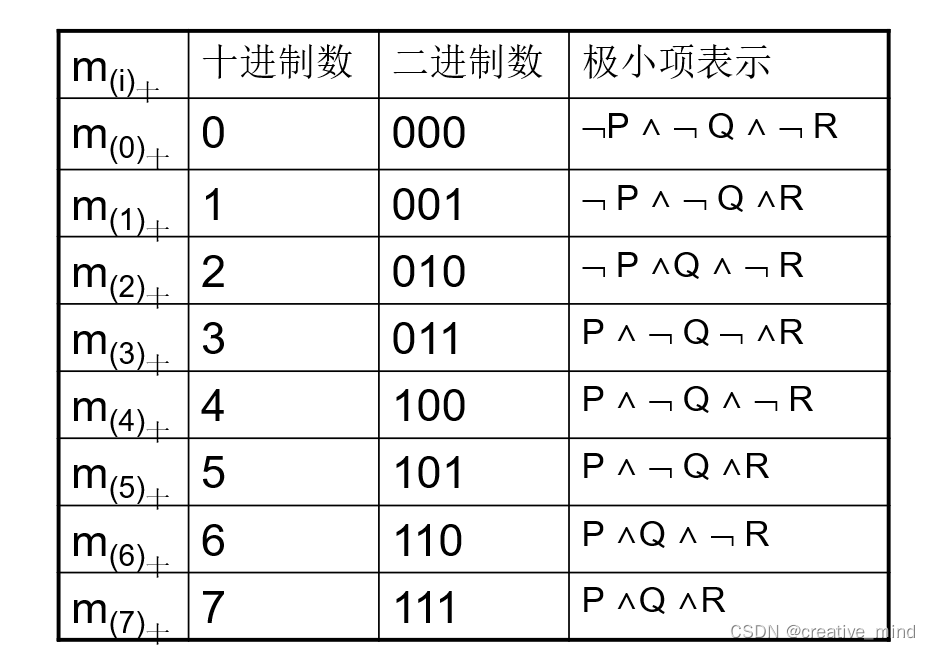
注意：极大项和极小项编码约定刚好相反

一些推论：

1，只要命题公式不是永真式，则一定可以写出对应与其等价的唯一的主合取范式

2，若命题公式为含有ｎ个变元的永假式，则主合取范式包含了2n个极大项的合取式。

3，可用主合取范式判定二个命题公式是否等价

4，已知一个命题公式的主析取范式，则一定可以直接写出与其等价的主合取范式来。反之也行。

5，对应于有ｎ个变元的命题公式，则一定有：主析范式极小项数＋主合范式极大项数＝　2^n

主范式的个数

一个原子命题变元有四个不同的真值表（4^1个）；

二个原子命题变元有16个不同的真值表（4^2个）；

以此类推，若有ｎ个变元的命题公式，则可构成4^n个不同的真值表。

对于含有ｎ个变元的命题公式，必定可写出4^n个主范式，若排除永真式或永假式，则实际可写出（ 4^n －１）个主析（或主合）范式。　

下一次我将分享，推理理论。

请大家多多支持！