在近日由 137Labs 发起,Cointime 主持的 Layer2 生态专场讨论中,OKLink 产品经理 Selina Wang
从产品数据与生态发展的角度带来分享,超过11万 Web3 用户共同收听参与。(以下为直播问答摘录)
在近日由 137Labs 发起,Cointime 主持的 Layer2 生态专场讨论中,OKLink 产品经理 Selina Wang
从产品数据与生态发展的角度带来分享,超过11万 Web3 用户共同收听参与。(以下为直播问答摘录)
以太坊Layer2的生态现状和发展的趋势如何?

据统计,目前 Layer2 的总 TVL 已接近390亿美元,自市场回暖以来呈指数级增长,已上线或即将上线的项目超过100个。随着坎昆升级的发生,所有 Layer2 项目将变得更有竞争力,我们可能会见证一个所谓的“Rollup 夏季”。在这样的背景下,OKLink 也为大家整理了坎昆专题页,将帮助大家了解坎昆升级的关键协议变更、Blob 等,以及升级对 TPS、费用和价格等数据指标的影响。我们同时展示主流 Layer2 供应链的对比数据,以及升级前后的情况,让大家第一时间获取这些信息。
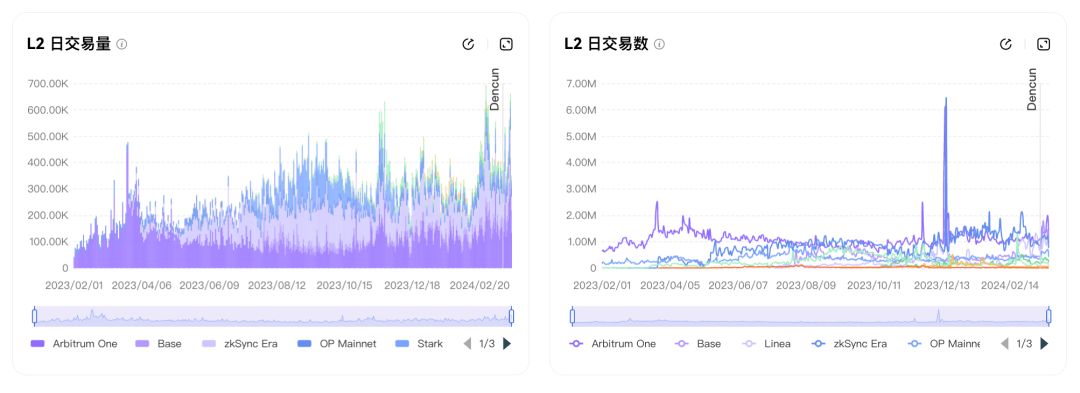 OKLink Dencun升级专题:https://www.oklink.com/cn/eth/dencun-upgrade
OKLink Dencun升级专题:https://www.oklink.com/cn/eth/dencun-upgrade
Scroll生态在Layer2中的竞争地位如何?
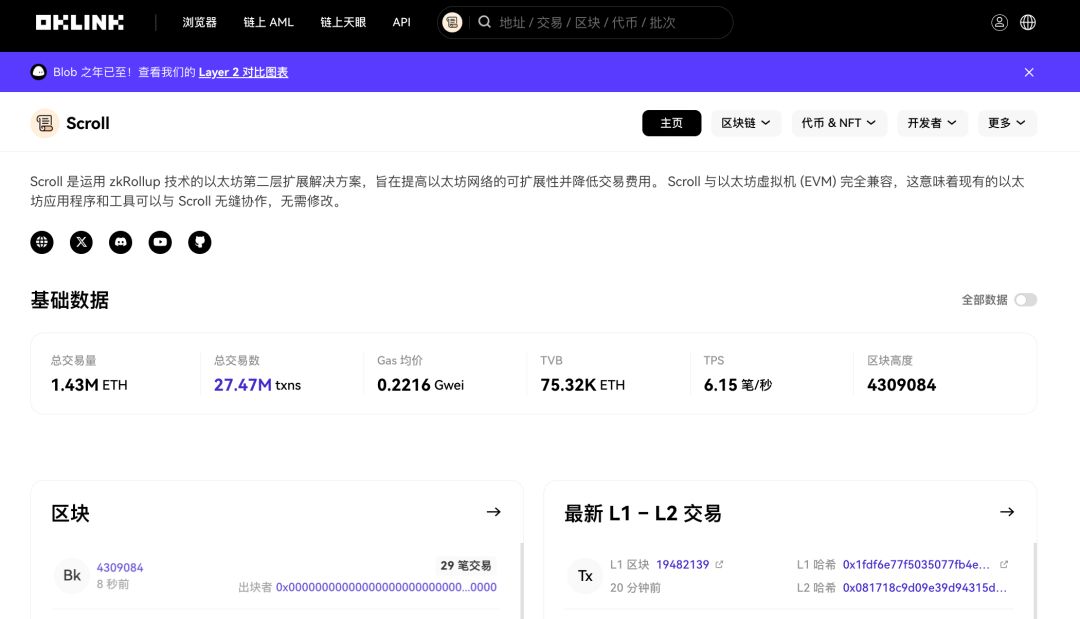 OKLink Scroll浏览器
在生态建设方面,Scroll 注重社区驱动,并积极布局链上生态。他们的社区非常活跃,团队经常与合作伙伴和开发者深入讨论,以开发出真正符合用户需求的产品。尽管以太坊 Layer2 的竞争激烈,但我相信凭借 Scroll 的优势,它可以脱颖而出。
Scroll 由于与以太坊高度兼容,因此吸引了许多项目方、开发者和 DApp 来部署和合作。在我们 OKLink 这边也有一些数据支持这个观点,即在我们的 Scroll 浏览器首页可以看到,Scroll的地址总数已经超过了 340 万,总交易数量也超过了 2,500 万笔。部署的合约数量达到了 10056 万,还有超过 10 万个代币。这些数据都在持续呈现增长趋势,说明 Scroll 生态中的开发者和交互地址都在不断增长。
此外,Scroll 这条链本身的技术背景非常强大,创始人在 2024 年公布了他们将围绕四个垂直领域进行技术发展和规划:速度更快、成本更低、更去中心化以及更安全。这些方面对于普通用户和开发者都是非常重要的,他们还计划为 EVM 添加新功能,进行一些创新性的实验。
OKLink Scroll浏览器
在生态建设方面,Scroll 注重社区驱动,并积极布局链上生态。他们的社区非常活跃,团队经常与合作伙伴和开发者深入讨论,以开发出真正符合用户需求的产品。尽管以太坊 Layer2 的竞争激烈,但我相信凭借 Scroll 的优势,它可以脱颖而出。
Scroll 由于与以太坊高度兼容,因此吸引了许多项目方、开发者和 DApp 来部署和合作。在我们 OKLink 这边也有一些数据支持这个观点,即在我们的 Scroll 浏览器首页可以看到,Scroll的地址总数已经超过了 340 万,总交易数量也超过了 2,500 万笔。部署的合约数量达到了 10056 万,还有超过 10 万个代币。这些数据都在持续呈现增长趋势,说明 Scroll 生态中的开发者和交互地址都在不断增长。
此外,Scroll 这条链本身的技术背景非常强大,创始人在 2024 年公布了他们将围绕四个垂直领域进行技术发展和规划:速度更快、成本更低、更去中心化以及更安全。这些方面对于普通用户和开发者都是非常重要的,他们还计划为 EVM 添加新功能,进行一些创新性的实验。
如何参与并从Scroll等Layer2生态中获得财富机会?
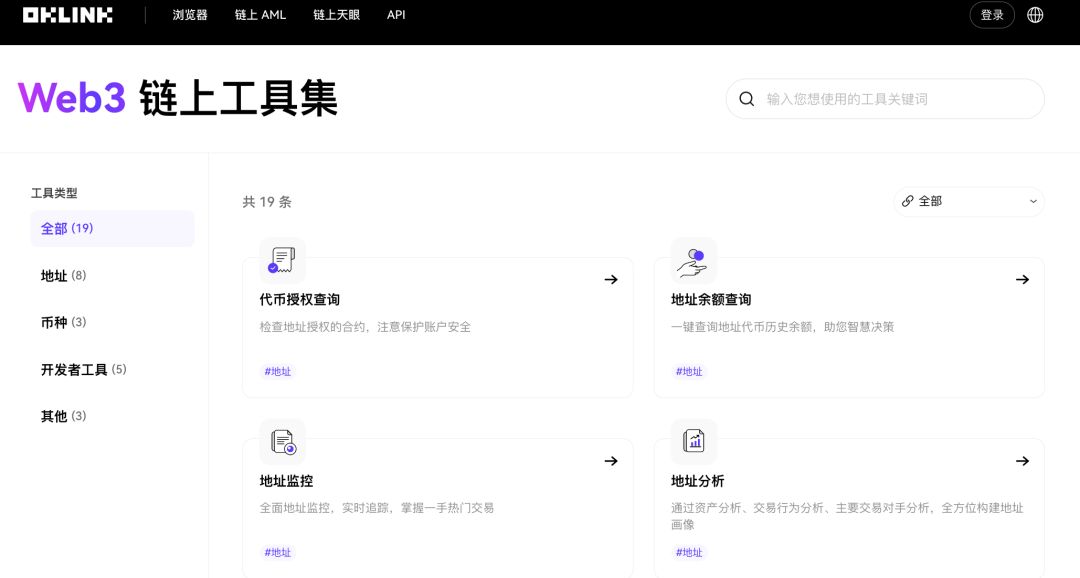 https://www.oklink.com/cn/tools
此外,关注交易数量、合约地址数等数据也是很好的助手,可以为投资决策提供辅助信息。通过观察这些数据,投资者可以更好地了解市场的活跃程度和项目的发展情况,从而做出更明智的投资决策。
最后,积极参与社区活动也是深度参与 Web3 的重要途径。在社区里和其他成员交流,了解不同项目的发展动向,可以帮助投资者更全面地了解市场和项目,从而找到更多的投资机会。
欧科云链致力于提供领先的链上数据与安全服务。OKLink 作为全球领先的 Web3 数据分析平台,提供当前全网数据最为丰富而全面的浏览器数据服务。
点击左下角「阅读原文」,开启全维度数据之旅。
https://www.oklink.com/cn/tools
此外,关注交易数量、合约地址数等数据也是很好的助手,可以为投资决策提供辅助信息。通过观察这些数据,投资者可以更好地了解市场的活跃程度和项目的发展情况,从而做出更明智的投资决策。
最后,积极参与社区活动也是深度参与 Web3 的重要途径。在社区里和其他成员交流,了解不同项目的发展动向,可以帮助投资者更全面地了解市场和项目,从而找到更多的投资机会。
欧科云链致力于提供领先的链上数据与安全服务。OKLink 作为全球领先的 Web3 数据分析平台,提供当前全网数据最为丰富而全面的浏览器数据服务。
点击左下角「阅读原文」,开启全维度数据之旅。