一、三角系统

……

二、高斯消元法

……

三、LU分解--直接三角分解法 求解线性方程Ax=b：

参考视频：【数值分析】矩阵LU三角分解| 速成讲解 考试宝典_哔哩哔哩_bilibili

令A=L·U，其中L是单位下三角矩阵（对角线上元素都是1），U是上三角矩阵。

无论矩阵A是多少，都有唯一的单位下三角矩阵L和上三角矩阵U，使得A可以分解为L·U。

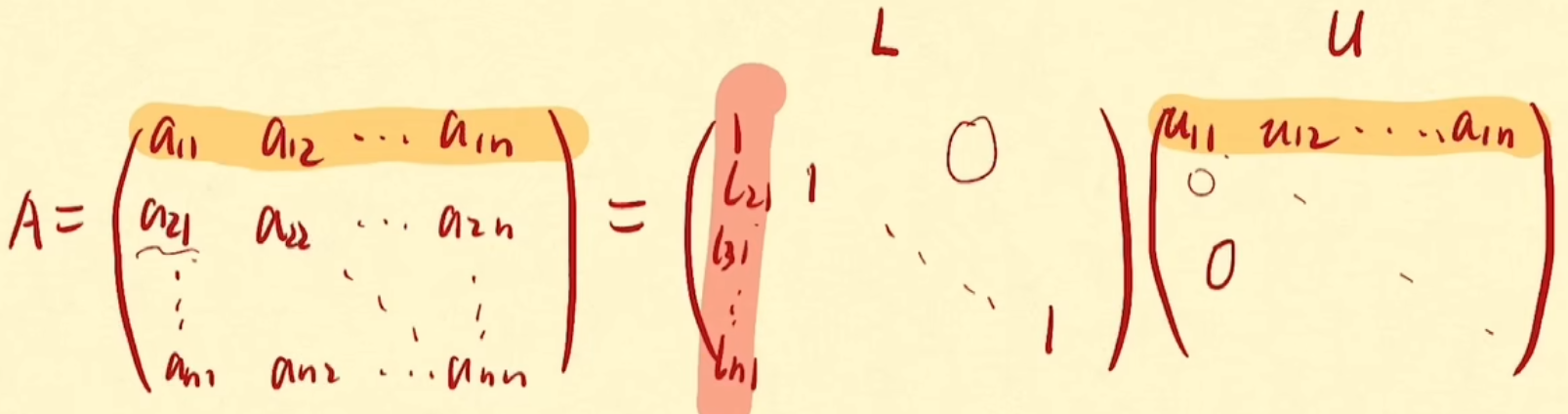由矩阵乘法可推出：

1.矩阵U的第一行元素等于矩阵A的第一行元素，即a1i=u1i，i=1,2……,n

2.矩阵L的第一列元素等于矩阵A的第一列元素除以u11，即li1=ai1/u11，i=1,2……,n

L是单位下三角矩阵 对角线上元素都是1，即lii=1 ，i=1,2……,n 

U是上三角矩阵。所以矩阵中的未知元素其实就不多了。

由于Ax=b即L·Ux=b

令Ly=b，Ux=y

第一步：首先根据A=L·U，可以很快推导出唯一的单位下三角矩阵L和唯一的上三角矩阵U

第二步：已知单位下三角矩阵L和向量b，根据Ly=b，很方便就求出y=(y1,y2,y3)^T

第三步：已知上三角矩阵U和向量y，根据Ux=y，很方便就求出x=(x1,x2,x3)

至此，线性方程求解完毕。

动手实操一下，就能清晰掌握了：

 第一步：根据A=L·U，推出矩阵L和U

第二步：根据Ly=b 求出y

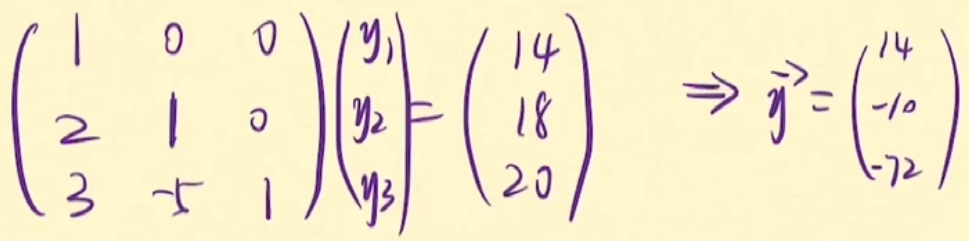
第三步：根据Ux=y 求出x

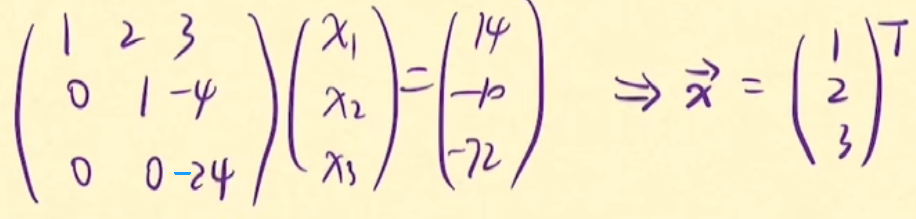
向量x求解完毕。

四、部分选主元的 LU 分解

……

五、LDM 分解, 对称矩阵的 LDL 分解，正定矩阵的 Choleskey 分解

……

六、其他线性系统，如带状系统

……