总结
本系列是机器学习课程的系列课程,主要介绍机器学习中无监督算法,包括划分聚类等。
参考
数据分析实战 | K-means算法——蛋白质消费特征分析
欧洲48国英文名称的来龙去脉及其国旗动画
Kmeans在线动态演示
本门课程的目标
完成一个特定行业的算法应用全过程:
懂业务+会选择合适的算法+数据处理+算法训练+算法调优+算法融合
+算法评估+持续调优+工程化接口实现
机器学习定义
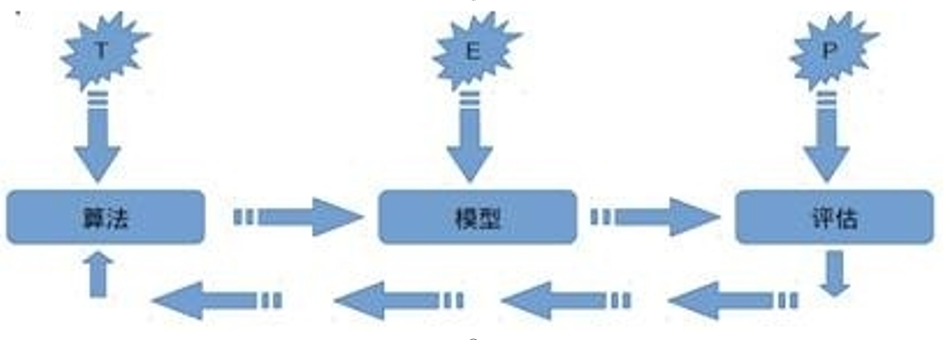
关于机器学习的定义,Tom Michael Mitchell的这段话被广泛引用:
对于某类任务T和性能度量P,如果一个计算机程序在T上其性能P随着经验E而自我完善,那么我们称这个计算机程序从经验E中学习。
无监督算法
无监督概述








无监督中的数据结构

虽然是聚类,依然有参数需要输入、限制条件,需要预先设置的参数越少越好。 对应隐藏模式发现
噪声数据解释:
顺序不敏感, 前面提到聚类算法多种多样,各有取舍,有些算法就存在对





划分聚类Kmeans算法




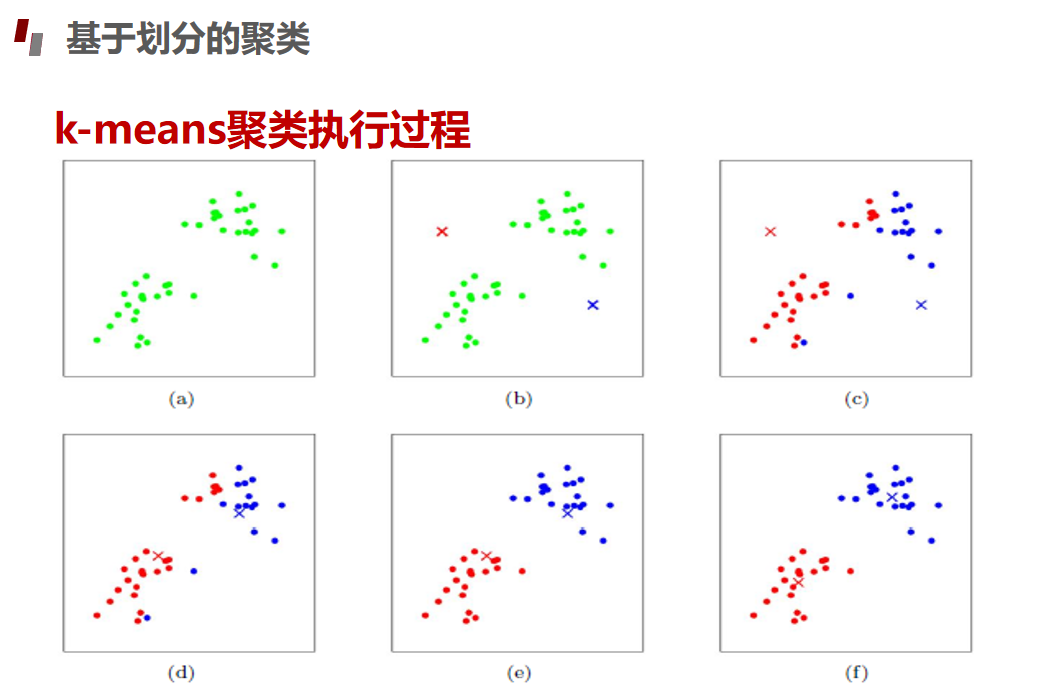


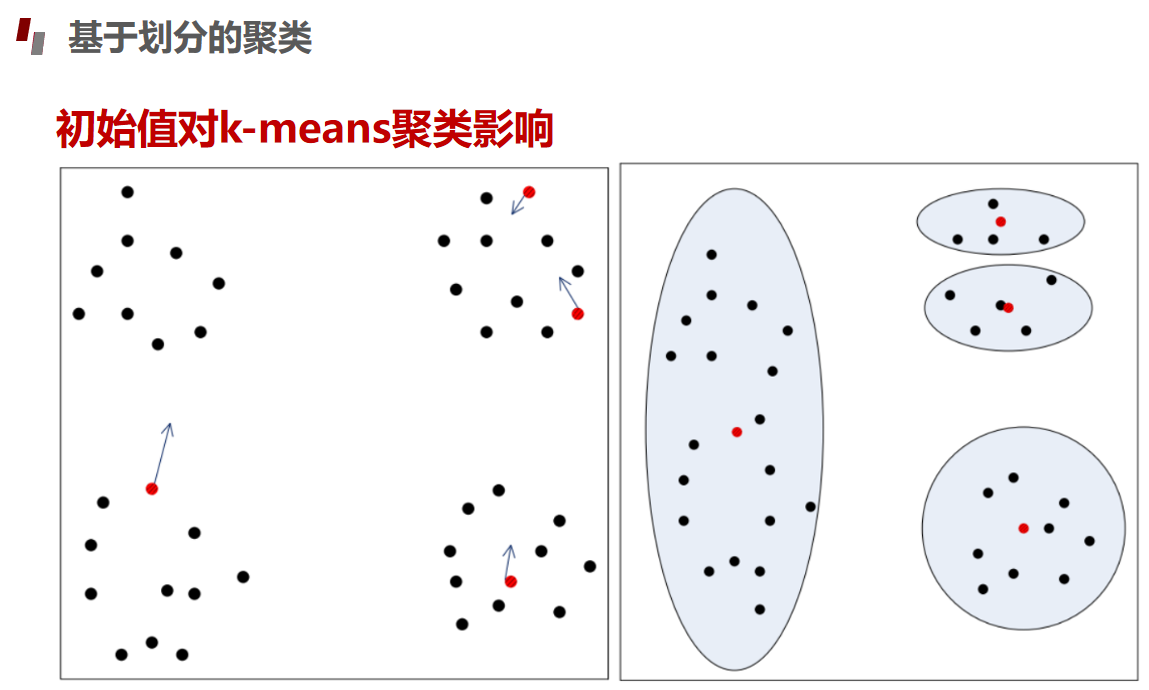
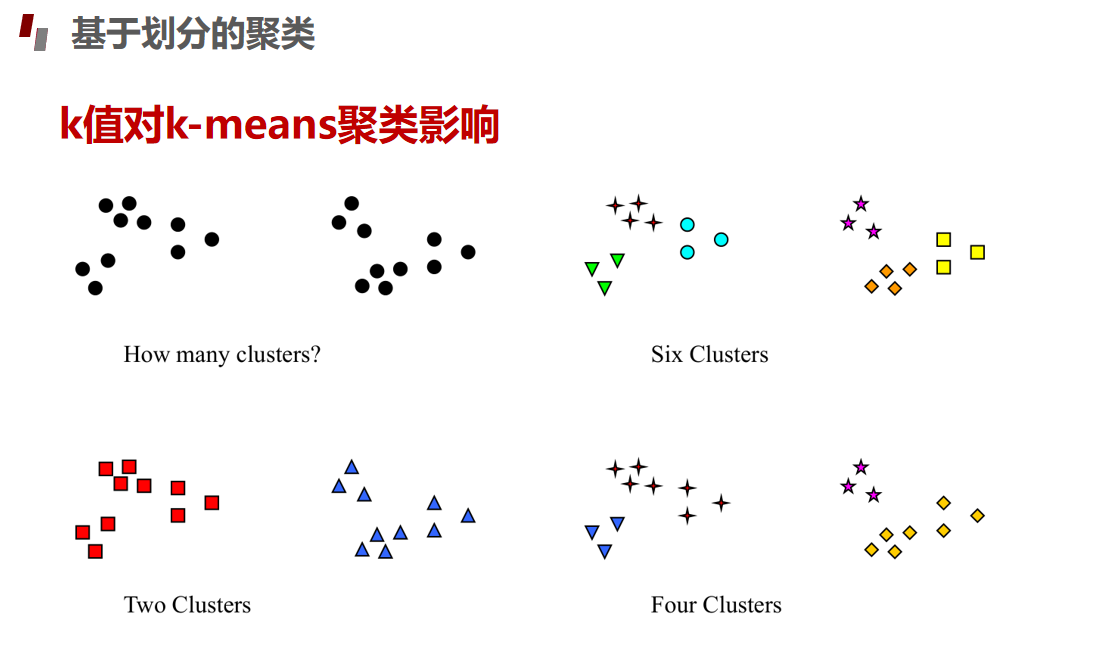

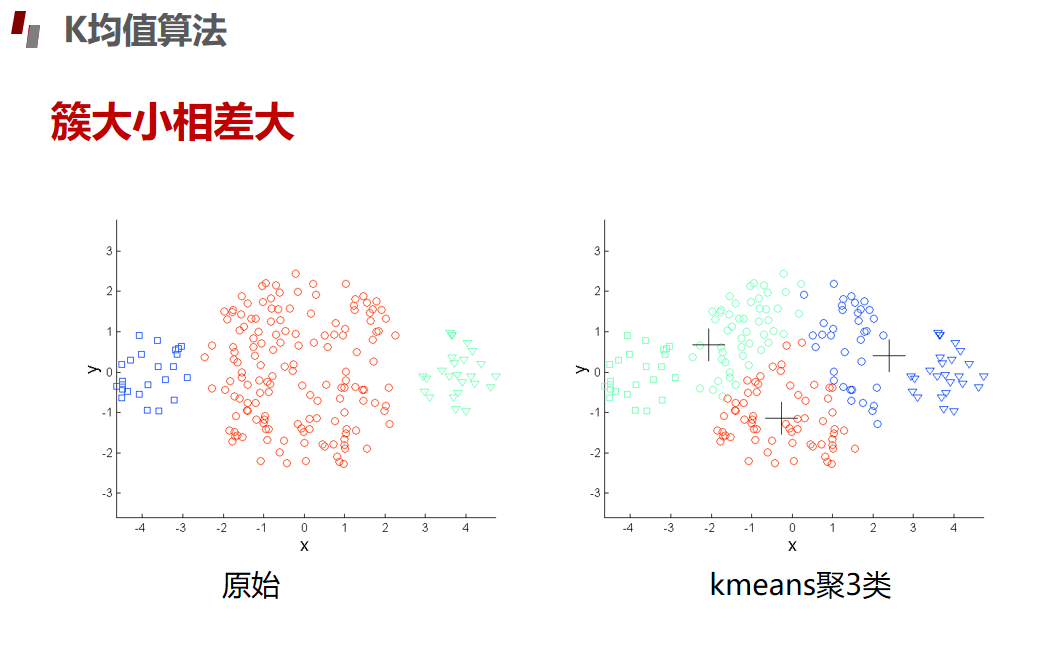
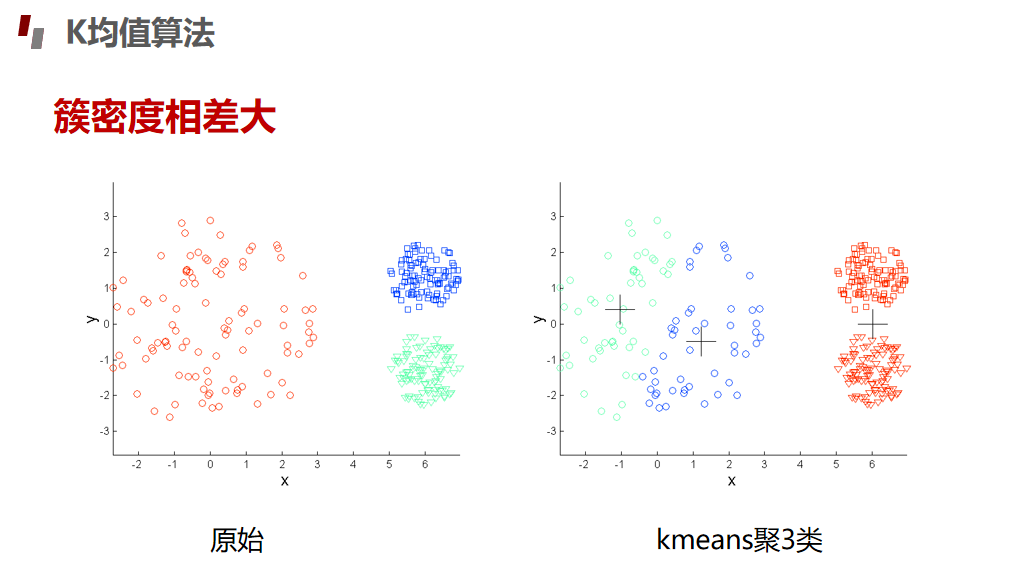
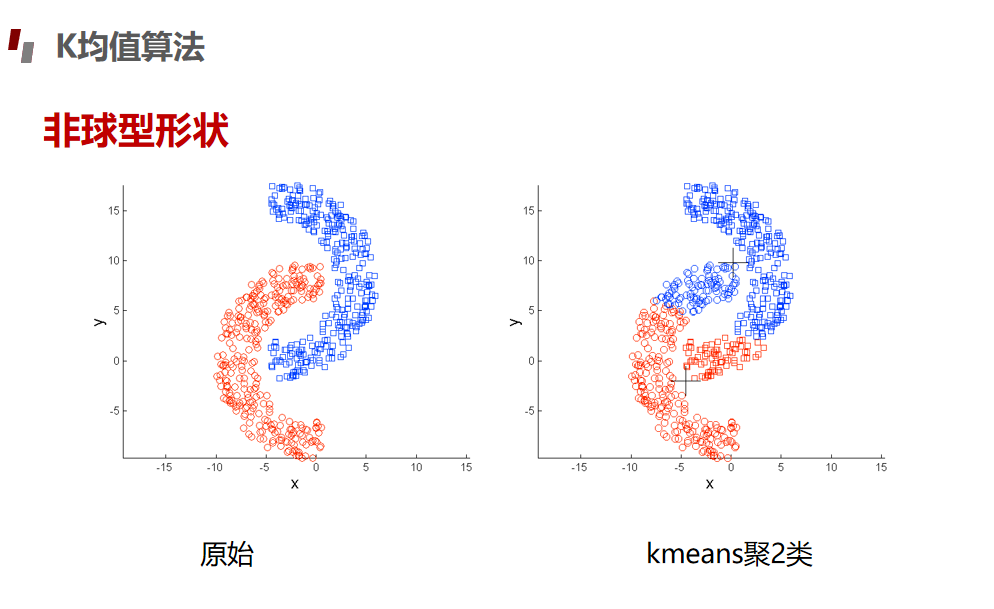
评估指标
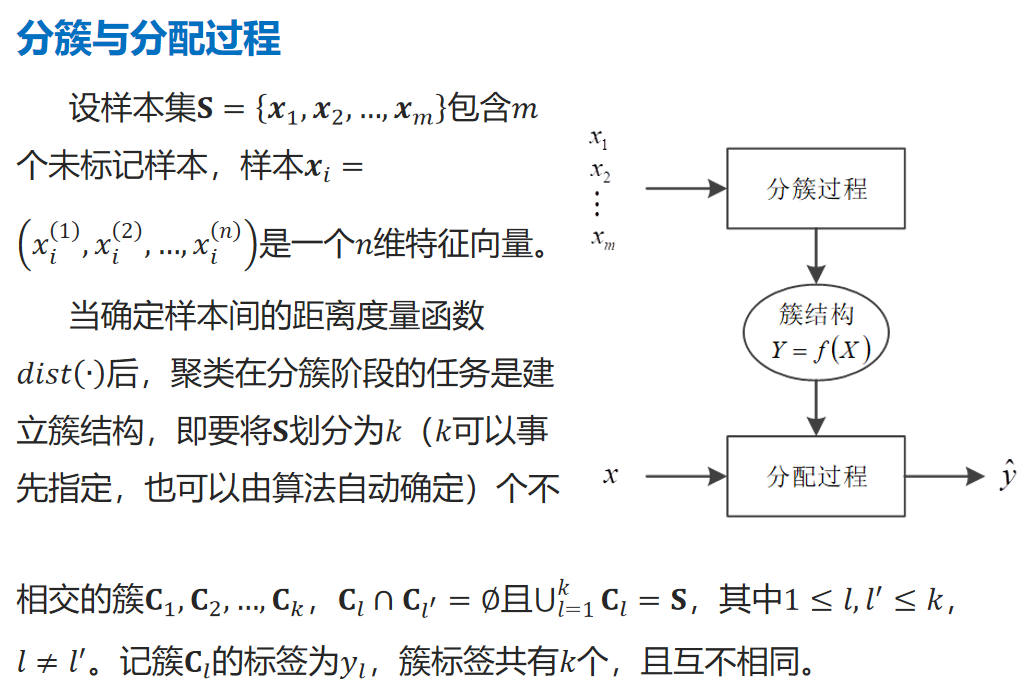
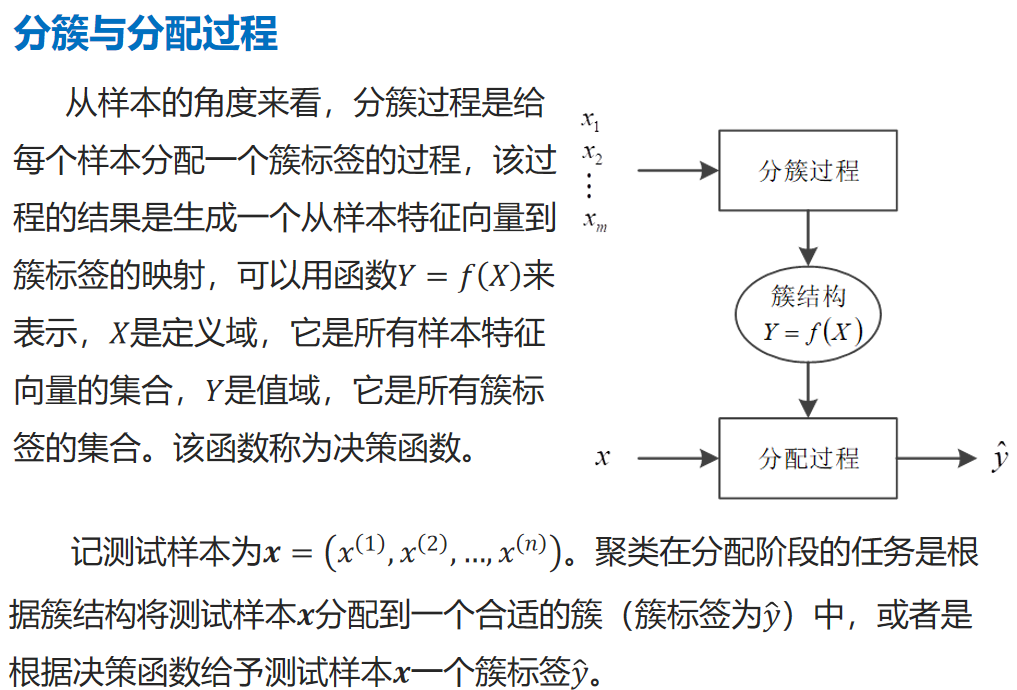
分簇与分配过程








轮廓系数



DB指数(Davies-Bouldin Index,DBI)

Dunn指数(Dunn Index,DI)

手机机主身份识别应用方案-学习过程

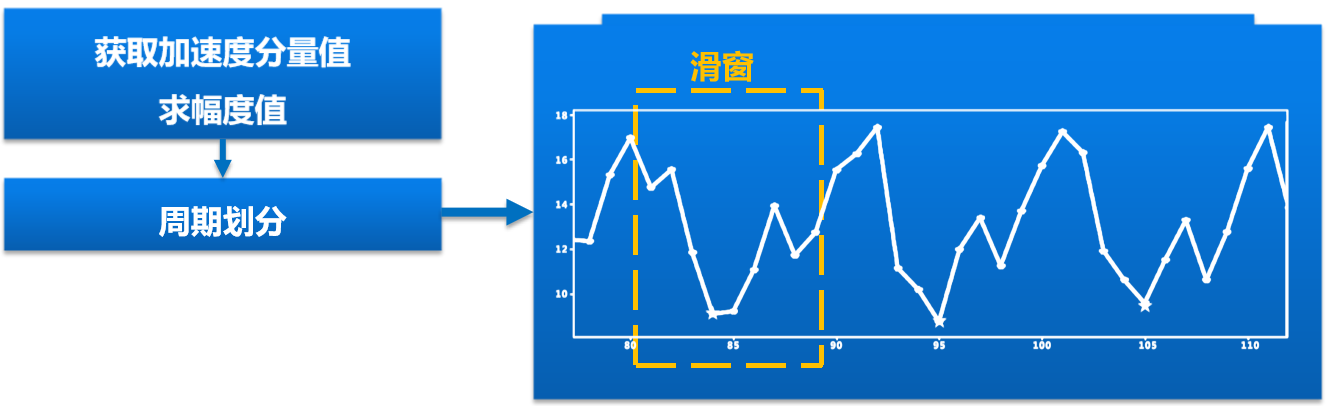

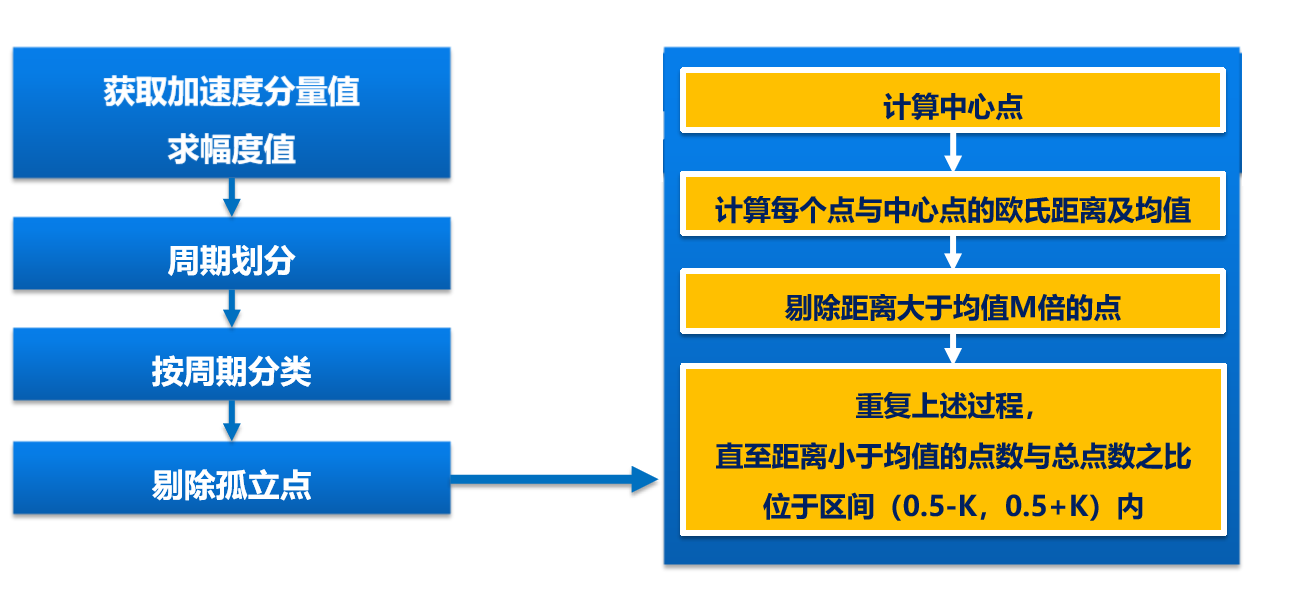
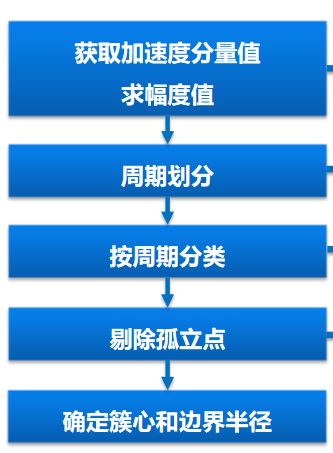
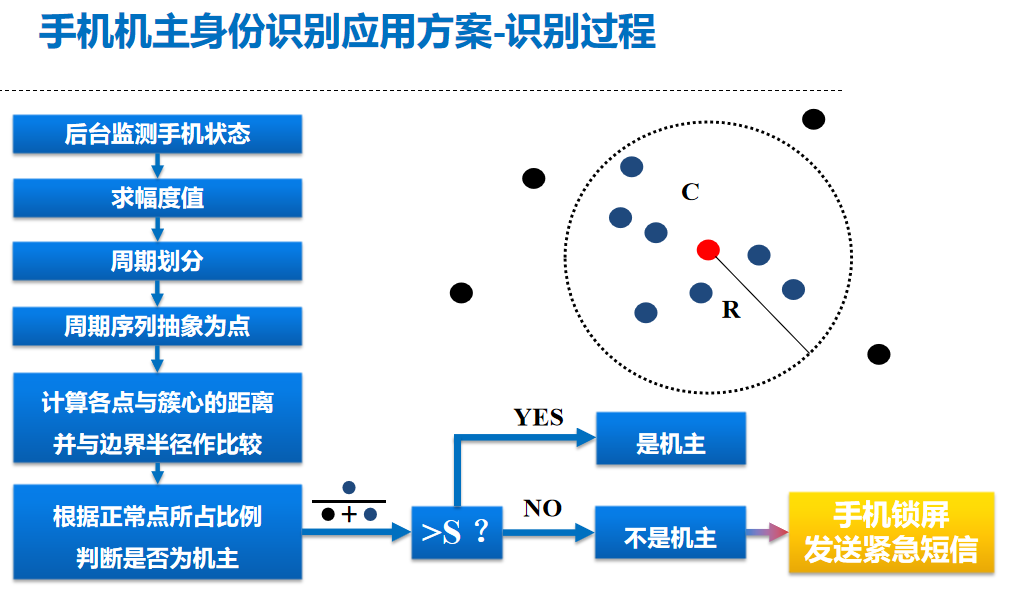
进一步讨论


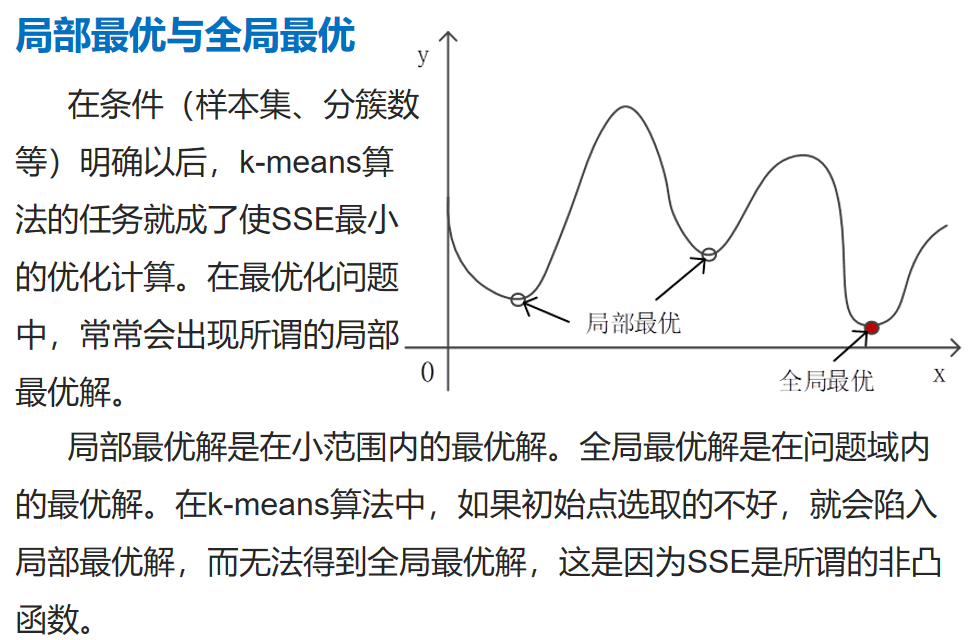

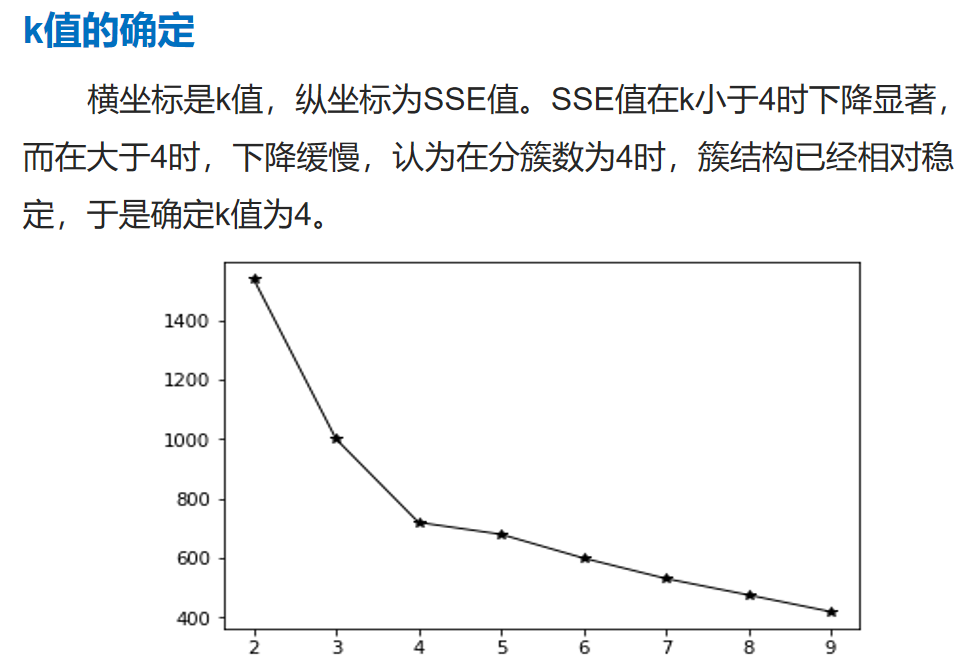

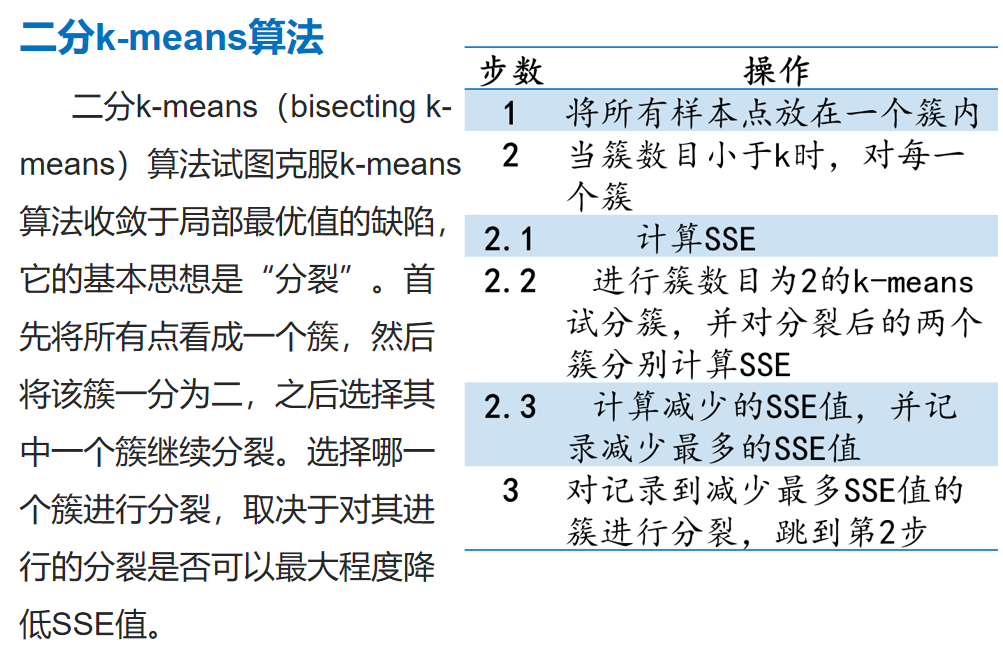
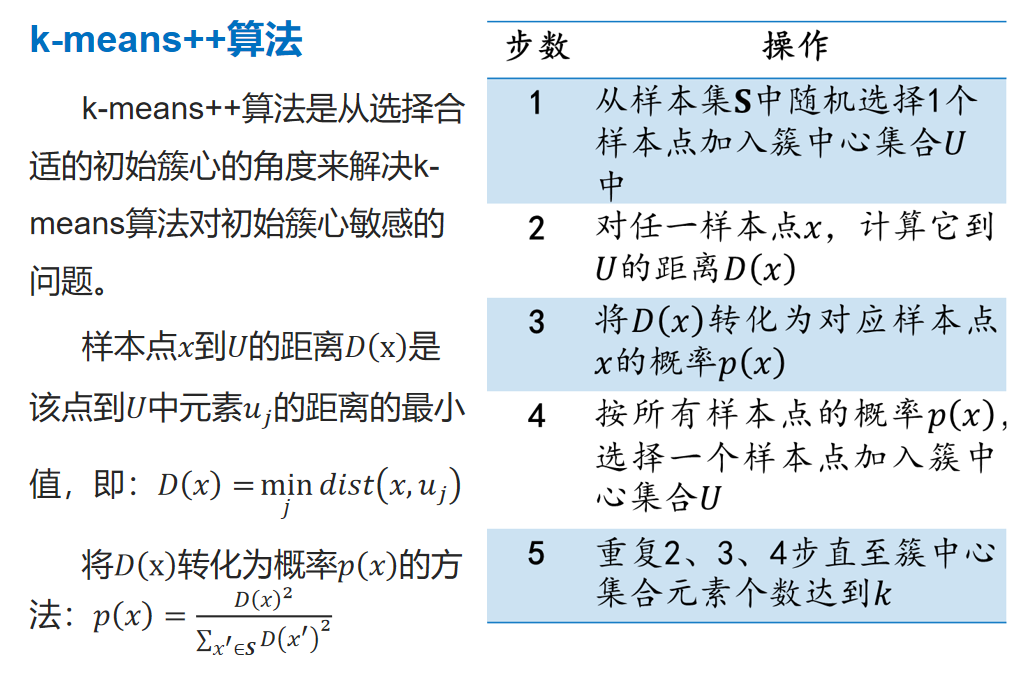
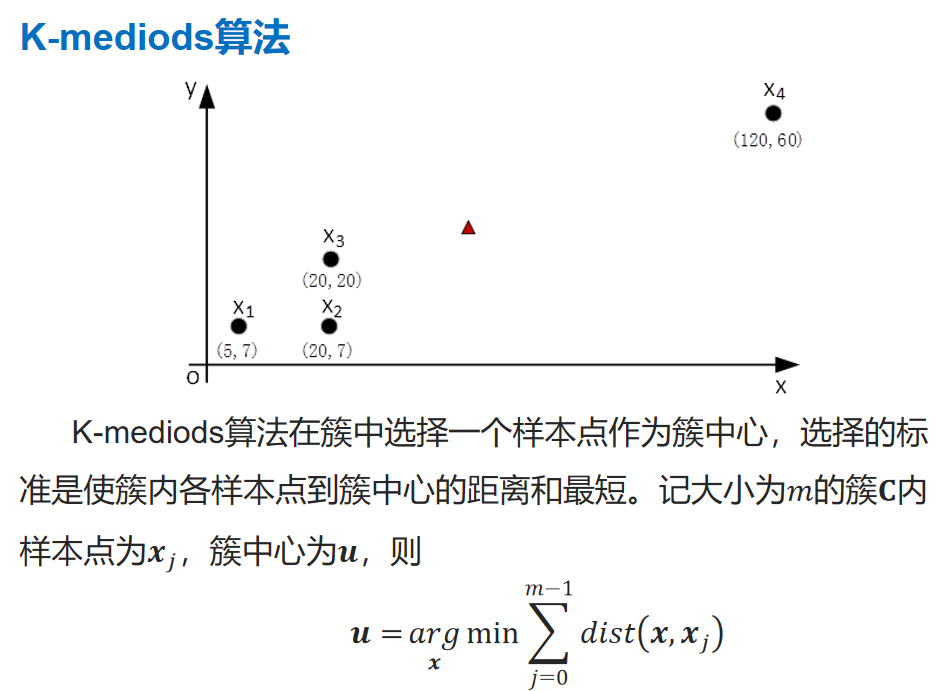
改进算法

划分聚类Kmeans算法案例
Kmeans案例
# 生成数据模块
from sklearn.datasets import make_blobs
# k-means模块
from sklearn.cluster import KMeans
# 评估指标——轮廓系数,前者为所有点的平均轮廓系数,后者返回每个点的轮廓系数
from sklearn.metrics import silhouette_score, silhouette_samples
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x_true, y_true = make_blobs(n_samples= 600
, n_features= 2, centers= 4, random_state= 1)
# 绘制出所生成的数据
plt.figure(figsize= (6, 6))
plt.scatter(x_true[:, 0], x_true[:, 1], c= y_true, s= 10)
plt.title("Origin data")
plt.show()
输出为:
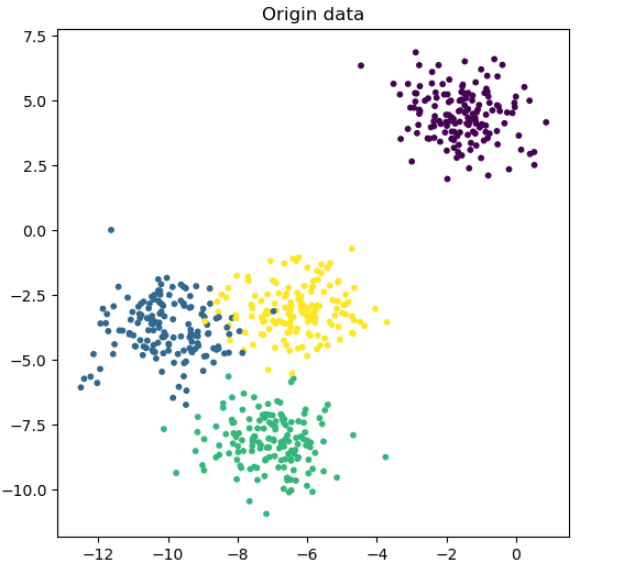
# 根据不同的n_centers进行聚类
n_clusters = [x for x in range(3, 6)]
for i in range(len(n_clusters)):
# 实例化k-means分类器
clf = KMeans(n_clusters= n_clusters[i])
y_predict = clf.fit_predict(x_true)
# 绘制分类结果
plt.figure(figsize= (6, 6))
plt.scatter(x_true[:, 0], x_true[:, 1], c= y_predict, s= 10)
plt.title("n_clusters= {}".format(n_clusters[i]))
ex = 0.5
step = 0.01
xx, yy = np.meshgrid(np.arange(x_true[:, 0].min() - ex, x_true[:, 0].max() + ex, step),
np.arange(x_true[:, 1].min() - ex, x_true[:, 1].max() + ex, step))
zz = clf.predict(np.c_[xx.ravel(), yy.ravel()])
zz.shape = xx.shape
plt.contourf(xx, yy, zz, alpha= 0.1)
plt.show()
# 打印平均轮廓系数
s = silhouette_score(x_true, y_predict)
print("When cluster= {}\nThe silhouette_score= {}".format(n_clusters[i], s))
# 利用silhouette_samples计算轮廓系数为正的点的个数
n_s_bigger_than_zero = (silhouette_samples(x_true, y_predict) > 0).sum()
print("{}/{}\n".format(n_s_bigger_than_zero, x_true.shape[0]))
输出为:
When cluster= 3
The silhouette_score= 0.6009420412542107
595/600
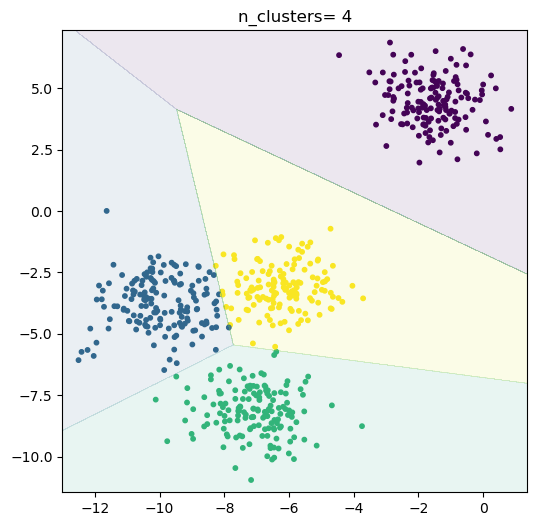
When cluster= 4
The silhouette_score= 0.637556444143356
599/600
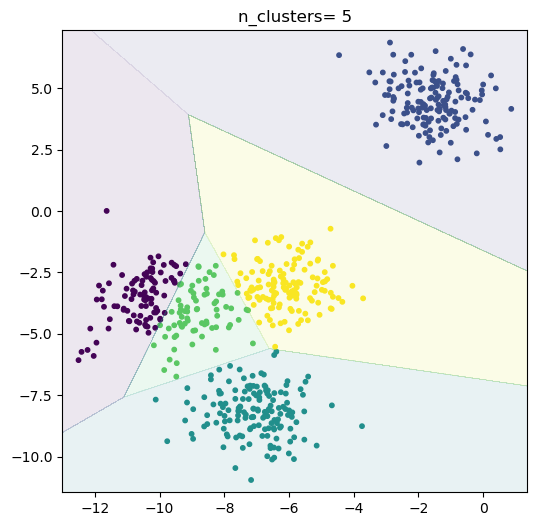
When cluster= 5
The silhouette_score= 0.5604812245680646
598/600
结论:预设4簇的时候其平均轮廓系数最高,所以分4簇是最优的,与数据集相匹配。
使用Numpy实现K_Means聚类:
STEP1:加载相关模块
import matplotlib.pyplot as plt
import numpy as np
import random
STEP2:使用欧式距离公式
def distance(x, y):
z = np.expand_dims(x, axis=1) - y
z = np.square(z)
z = np.sqrt(np.sum(z, axis=2))
return z
STEP3:簇中心更新函数
def k_means(data, k, max_iter=20):
data = np.asarray(data, dtype=np.float32)
n_samples, n_features = data.shape
# 随机初始化簇中心
indices = random.sample(range(n_samples), k)
center = np.copy(data[indices])
cluster = np.zeros(data.shape[0], dtype=np.int32)
i = 1
while i <= max_iter:
dis = distance(data, center)
# 样本新的所属簇
cluster = np.argmin(dis, axis=1)
onehot = np.zeros(n_samples * k, dtype=np.float32)
onehot[cluster + np.arange(n_samples) * k] = 1.
onehot = np.reshape(onehot, (n_samples, k))
# 以矩阵相乘的形式均值化簇中心
# (n_samples, k)^T * (n_samples, n_features) = (k, n_features)
new_center = np.matmul(np.transpose(onehot, (1, 0)), data)
new_center = new_center / np.expand_dims(np.sum(onehot, axis=0), axis=1)
center = new_center
i += 1
return cluster, center
STEP4:可视化
def scatter_cluster(data, cluster, center):
if data.shape[1] != 2:
raise ValueError('Only can scatter 2d data!')
# 画样本点
plt.scatter(data[:, 0], data[:, 1], c=cluster, alpha=0.8)
mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', '<b', 'pb']
# 画质心点
for i in range(center.shape[0]):
plt.plot(center[i, 0], center[i, 1], mark[i], markersize=20)
plt.show()
STEP5:训练
n_samples = 500
n_features = 2
k = 3
data = np.random.randn(n_samples, n_features)
cluster, center = k_means(data, k)
scatter_cluster(data, cluster, center)
STEP6:输出结果
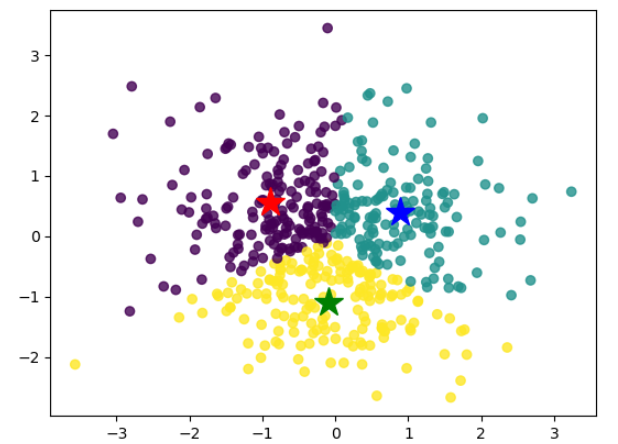
确定方向过程
针对完全没有基础的同学们
1.确定机器学习的应用领域有哪些
2.查找机器学习的算法应用有哪些
3.确定想要研究的领域极其对应的算法
4.通过招聘网站和论文等确定具体的技术
5.了解业务流程,查找数据
6.复现经典算法
7.持续优化,并尝试与对应企业人员沟通心得
8.企业给出反馈