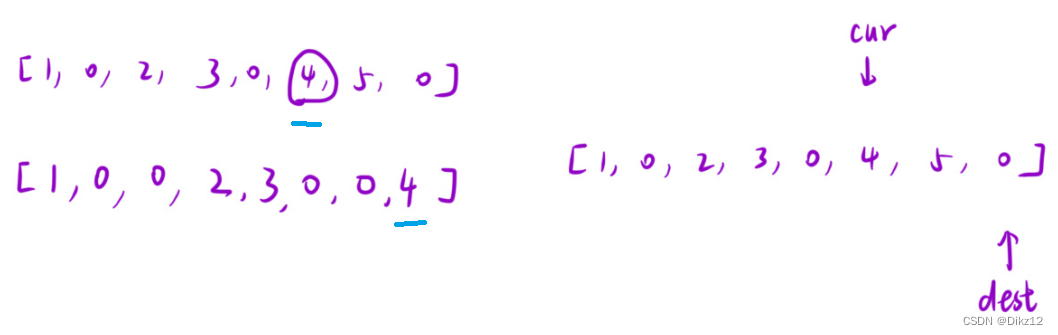- 🎥 个人主页:Dikz12
- 🔥个人专栏:Java算法
- 📕格言:那些在暗处执拗生长的花,终有一日会馥郁传香
- 欢迎大家👍点赞✍评论⭐收藏
目录
1. 移动零
1.1 题目描述
1.2 讲解算法原理
1.3 编写代码
2. 复写零
2.1 题目描述
2.2 讲解算法原理
2.3代码实现
3. 盛最多水的容器
3.1 题目描述
3.2 讲解算法原理
3.3 代码实现
4.有效三角形的个数
4.1 题目描述
4.2 讲解算法原理
4.3代码实现
1. 移动零
1.1 题目描述
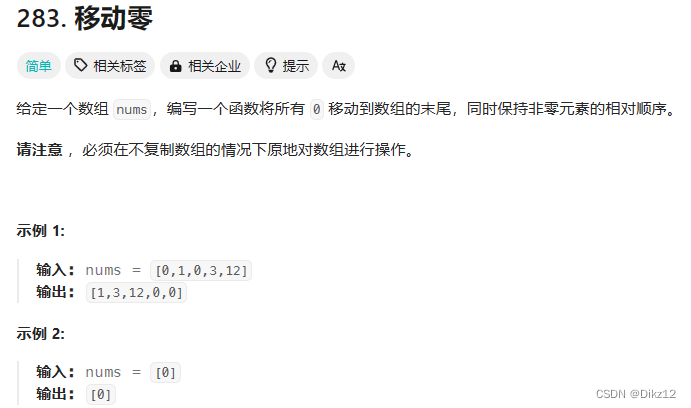
1.2 讲解算法原理
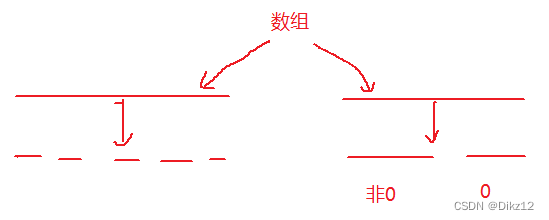
这种题型可以划分到:数组划分、数组分块. 解决这类题就有最经典的算法:双指针算法.
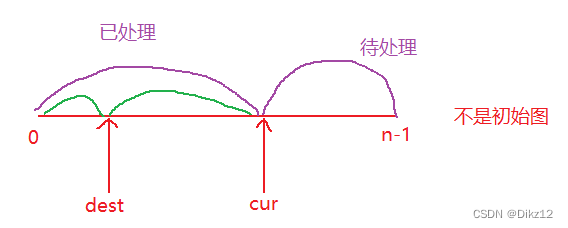
定义两个指针,作用:
- cur:从左到右扫描数组,遍历数组.
- dest:在已处理区间内,非0元素的最后一个位置.
如图数组被划分成了三个区间:[0,dest]:非0 ,[dest+1,cur-1]:0,[cur,n-1]:待处理.
做到代码按照上面思路走即可.
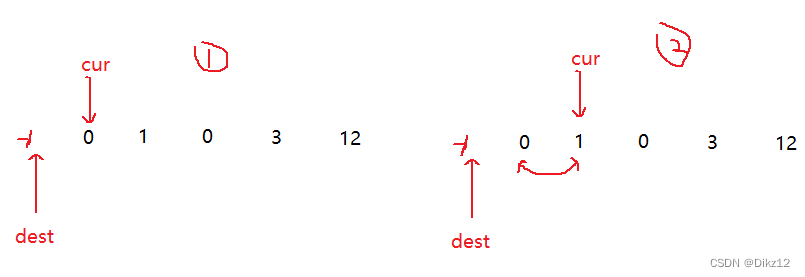
cur从前往后遍历的过程中:
- 遇到0元素,cur++
- 遇到非0元素,交换dest+1和cur的值
1.3 编写代码
public void moveZeroes(int[] nums) {
int dest = -1;
for(int cur = 0;cur < nums.length; cur++) {
if(nums[cur] != 0) {
dest++;
int tmp = nums[cur];
nums[cur] = nums[dest];
nums[dest] = tmp;
}
}
}2. 复写零
2.1 题目描述

2.2 讲解算法原理
思路:
如果「从前向后」进⾏原地复写操作的话,由于 0 的出现会复写两次,导致没有复写的数「被覆 盖掉」。
因此我们选择「从后往前」的复写策略。 但是「从后向前」复写的时候,我们需要找到「最后⼀个复写的数」,因此我们的⼤体流程分两 步:
- 先找到最后⼀个复写的数;
- 然后从后向前进⾏复写操作
整体流程:
- 初始化两个指针, cur = 0,dest = -1;
- 找到最后一个复写的数;当cur < n时,判断cur位置的元素,是0的话dest,往后移动两步;不为0,移动一位;当dest走到最后一个位置或者等于数组长度,就breadk结束循环,否则,cur++
- 判断dest,是否越界.越界让最后一个位置的元素改成0,cur向前移动一位,dest 移动两位
- 从cur的位置开始往前遍历数组,cur 为0,把dest 和 dest -1位置的元素都改成0,移动两位;cur 不为0,dest位置的元素改为cur的,dest - -;
- cur--
2.3代码实现
public void duplicateZeros(int[] arr) {
int cur = 0, dest = -1, n = arr.length;
//1.找到复写之后数组的最后一个数
while(cur < n) {
if(arr[cur] == 0) {
dest += 2;
}else{
dest += 1;
}
if(dest >= n-1) {
break;
}
cur++;
}
//处理dest越界问题
if(dest == n) {
arr[n-1] = 0;
dest -= 2;
cur --;
}
//2.从后往前完成复写操作
while(cur >= 0){
if(arr[cur] != 0){
arr[dest--] = arr[cur--];
}else{
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}3. 盛最多水的容器
3.1 题目描述


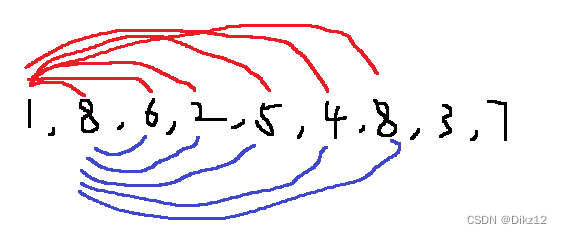
数组放的是高度:第0条线的高度是1,第1条线的高度是8........(对应的数组下标)。
如图:容器的height是由较低的的那条线决定的,而宽度这好等于右边下标减去左边下标.
3.2 讲解算法原理
解方法一: 暴力枚举.O(n^2)
先固定最左边的线1,依次枚举右边的线,所有容器都算一遍,记录最大值;在固定8,重复上诉过程.
解法二: 利用单调性,使用双指针解决.
- 取一部分区间进行模拟[6,2,5,4]
- 刚开始直接拿4和6,进行计算,V = h (高)* w (宽)
- 假设,4在向内枚举2和5时,不难发现宽始终在减少,高会有两种情况,遇见小的数,h 减少,w 减少,v一定减少;遇到大的数,h 不变,w减少,v减少
- 那较小的数向内枚举,v 始终是减少的.所以,可以直接把4干掉.
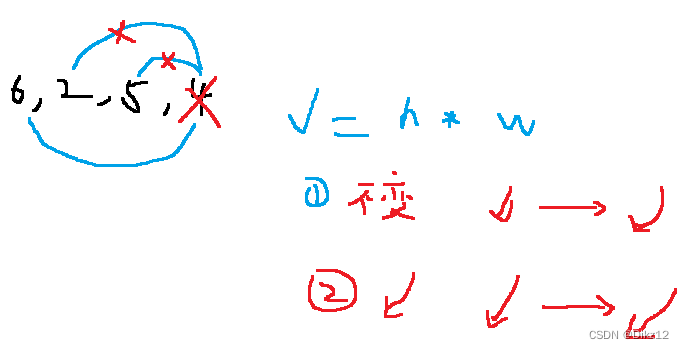
整体过程:
- 定义两个指针,left 指向最左边,right 指向最右边,初始容积为ret = 0;
- 高度取min(left,right),并记录目前的容积v,在max(v,ret)记录最大容积
- 左边高度小于右边,left--; 否则,right++ (相同,移动哪边都一样).
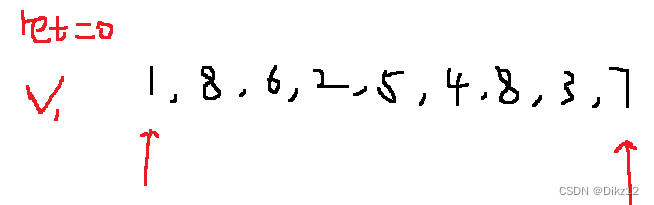
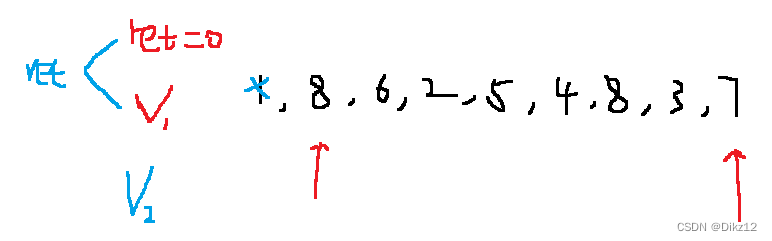
3.3 代码实现
public int maxArea(int[] height) {
int left = 0,right = height.length - 1,ret = 0;
while(left < right) {
int v = Math.min(height[left],height[right]) * (right - left);
ret = Math.max(ret,v);
if(height[left] < height[right]) {
left++;
}else {
right--;
}
}
return ret;
}4.有效三角形的个数
4.1 题目描述

4.2 讲解算法原理
解法一:暴力解法.O(n^3)
三层for循环,一层固定一个数 .
伪代码:
for(i = 0; i < n; i++)
for(j = i + 1; j < n; j++)
for(int k = j + 1; k < n; k++)
check(i,j,k)解法二: 利用单调性,使用双指针来解决问题.

如图,假设选取的三个数是有序的,就会发现第二种情况和第三种情况下,C已经是最大值了,无论加谁都是大于第三个数的.
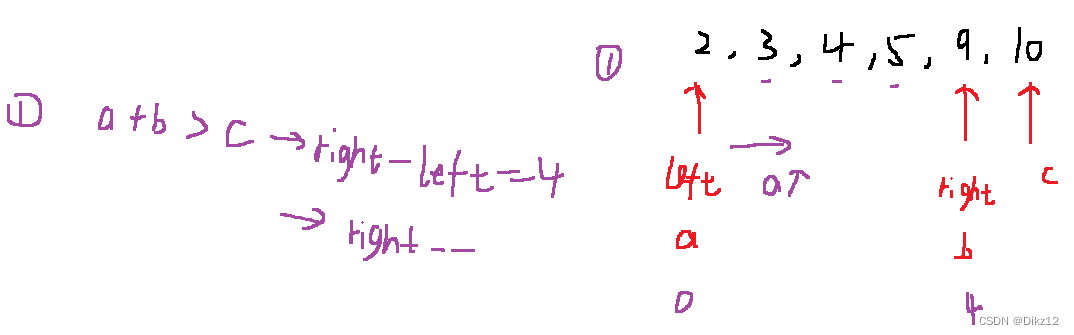
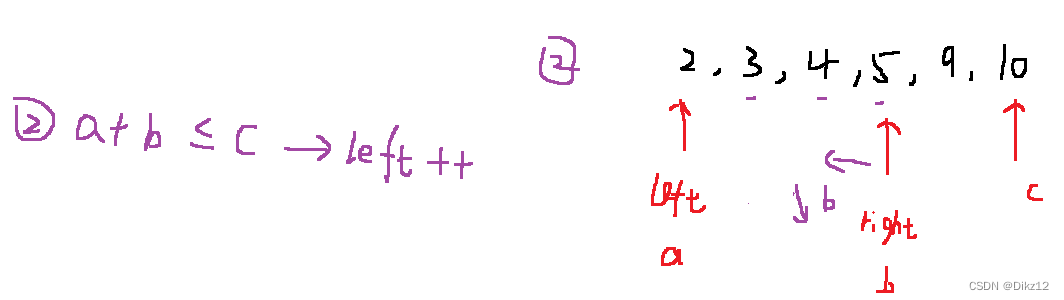
- 对数组进行排序
- 开始:count 统计个数; 固定一个最大的数(最右边),left指向最左边 ,right 指向最大数减一的位置.
- 在最大数区间内,使用双指针算法,快速统计符合要求的个数. (循环上图过程)
4.3代码实现
public int triangleNumber(int[] nums) {
//排序
Arrays.sort(nums);
int count = 0,n = nums.length;
//利⽤双指针快速统计出符合要求的个数
for(int i = n - 1; i >= 2; i--) {
int left = 0,right = i - 1;
while(left < right) {
if(nums[left] + nums[right] > nums[i]) {
count += right - left;
right--;
}else{
left++;
}
}
}
return count;
}