函数运算算法合集06
- 1、树的基本运算
- 1.1 树的存储结构
- 1.1.1 双亲存储结构
- 1.1.2 孩子链存储结构
- 1.1.3 孩子兄弟链式存储结构
- 2、二叉树的顺序存储
- 2.1 二叉树顺序存储的结构体
- 2.2 顺序存储的基本思路
- 3、二叉树的链式存储
- 3.1 二叉树的链式存储的结构体
- 3.2 链式存储的基本算法
- 3.2.1 初始化
- 4、二叉树的先/中/后序遍历
- 4.1 二叉树的先序遍历
- 4.2 二叉树的中序遍历
- 4.3 二叉树的后序遍历
- 4.4 二叉树的层序遍历
注:
本篇文章的概念合集
数据结构的概念大合集06(树和二叉树)
1、树的基本运算
1.1 树的存储结构
1.1.1 双亲存储结构
双亲存储结构是一种顺序存储结构,用一组连续空间存储树的所有结点,同时在每个节点中附设一个伪指针指示器双亲结点的位置(除头结点以为,每个节点只有唯一的双亲结点,将更结点的双亲结点的位置设置为特殊值-1);
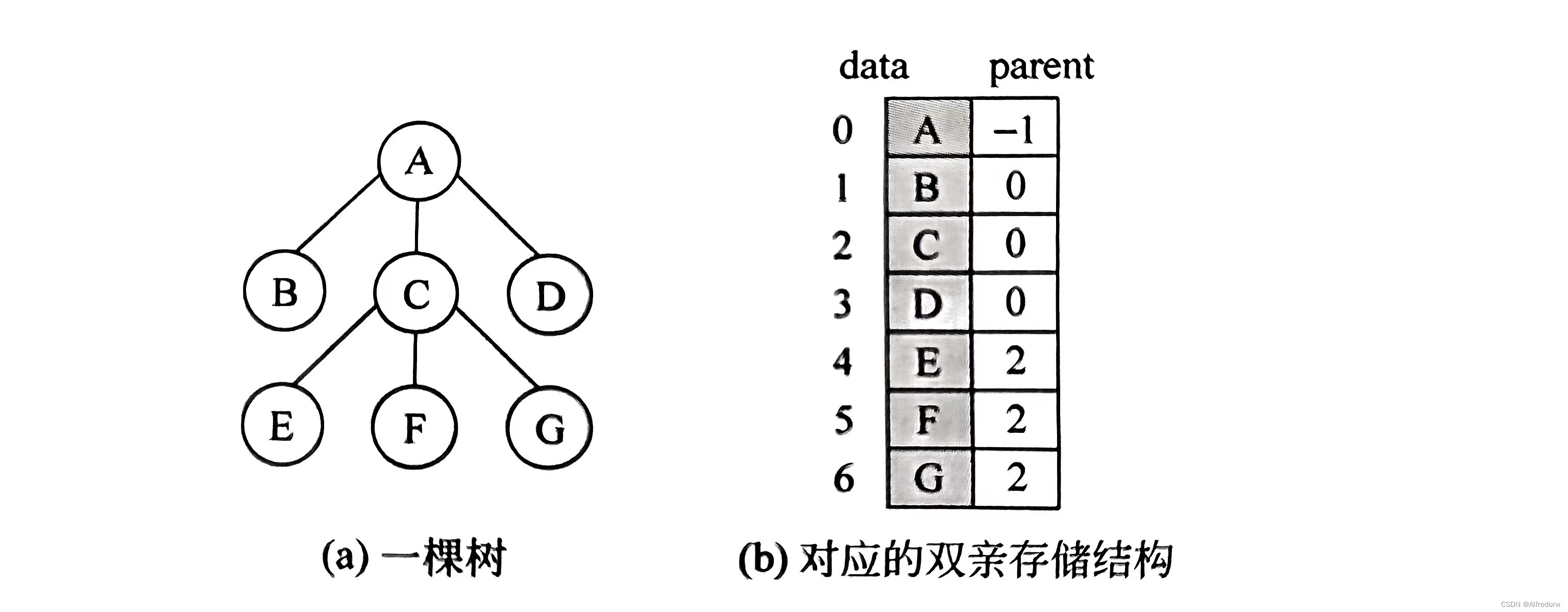
这种存储结构利用了每个节点(除根节点外)只有唯一双亲的性质。在这种存结构里面,求某个结点的双亲结点非常容易,但是求某个结点的孩子结点时就需要遍历整个存储结构。
//双亲存储结构
//双亲存储结构
typedef struct
{
ElemType data; //存放结点的值
int parent; //存放双亲的位置
}PTree[MaxSize];
1.1.2 孩子链存储结构
孩子链存储结构,每个结点不仅包含结点值,还包含指向所有孩子结点的指针,为避免由于树中每个结点的子树的个数不同导致算法的实现变化,最好将孩子链存储结构按树的度来设计结点的孩子结点的指针域的个数。
孩子链存储结构的优点是查找某结点的孩子结点十分方便,其缺点是查找某结点的双亲结点需要遍历数,且当树的度比较大时,存在较多的空指针域。
//孩子链存储结构
typedef struct node
{
ElemType data; //结点的值
struct node *sons[MaxSize]; //指向孩纸结点的指针
}TSonNode;
1.1.3 孩子兄弟链式存储结构
孩子兄弟链式存储结构,是将每个结点设计3个域,即一个数据元素域,一个指向该结点的左边第一个孩子结点的指针域,一个指向结点的下一个兄弟结点的指针域。
其优缺点与孩子链存储结构一样;孩子兄弟链式存储结构还有一个优点就是把该树转化为二叉树的存储结构。
这下来我们来介绍二叉树的相关内容。
//孩子兄弟链存储结构
typedef struct tnode
{
ElemType data; //结点的值
struct tnode * hp; //指向兄弟结点
struct tnode * vp; //指向孩子结点
}TSBnode;
2、二叉树的顺序存储
2.1 二叉树顺序存储的结构体
让二叉树按照从上之下,从左至右的顺序依次存储各个结点
//二叉树的顺序存储的结构体
typedef struct
{
ElemType value; //存放结点的值
bool isEmpty; //结点是否为空
}TreeNode[MaxSize];
开发技巧

2.2 顺序存储的基本思路
i是结点的编号
- i 的左孩子 —— 2i
- i 的右孩子 —— 2i + 1
- i 的父节点 —— [ i / 2 ]
- i 所在的层次 ——log2( n + 1 ) 或 log2n + 1
若是完全二叉树中共有n个结点,则
- 判断 i 是否有左孩子 —— 2i <= n
- 判断 i 是否有右孩子 —— 2i + 1 <= n
- 判断 i 是否是叶子/分支节点—— i > [n / 2]
若不是完全二叉树呢?
则将二叉树的结点编号与完全二叉树对应起来,则
- i 的左孩子 —— 2i
- i 的右孩子 —— 2i + 1
- i 的父节点 —— [ i / 2 ]
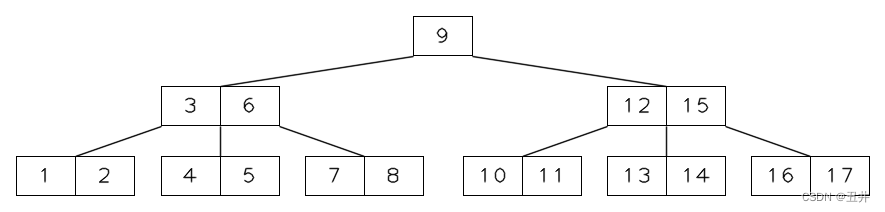
但是运用这种方式,如果二叉树的结点较少的话,此思路还是会开辟出一个类似于完全二叉树的内存,这样就会导致大量的内存浪费,比如下面图示

结论:
二叉树的顺序存储结构,只适合于存储完全二叉树。
3、二叉树的链式存储
3.1 二叉树的链式存储的结构体
//二叉树的链式存储的结构体
typedef struct BiTNode
{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左,右孩子指针
}BdiTnode, *BiTree;
3.2 链式存储的基本算法
3.2.1 初始化
// 初始化
BiTree root = NULL; // 定义一个指向根结点的指针,
root = (BiTree)malloc(sizeof(BiTNode)); // 分配根节点内存
if (root != NULL) { // 检查分配是否成功
root->data = 1; // 正确赋值
root->lchild = NULL;
root->rchild = NULL;
}
// 插入新结点
BiTNode *p = (BiTNode)malloc(sizeof(BiTNode)); // 分配新节点内存,注意,这里的p也是指针
if (p != NULL) { // 检查分配是否成功
p->data = 2; // 正确赋值
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; // 将新节点设置为根的左孩子
}
4、二叉树的先/中/后序遍历
运用二叉树的递归遍历特性确定的次序规则
二叉树的递归特性:
- 空二叉树
- 由“根节点 + 左子树 + 右子树”组成的二叉树
4.1 二叉树的先序遍历
- 若二叉树为空,则什么也不做;
- 若二叉树非空:
访问根节点(可对结点进行部分操作,比如输出结点的data值);
先序遍历左子树
先序遍历右子树
//先序遍历
void PreOrder(BiTree T)
{
if(T != NULL)
{
vist(T); //可以进行部分操作
PreOrder(T->lchild); //遍历左子树
PreOrder(T->rchild); //遍历右子树
}
}
先序遍历的空间复杂度是O(h)
脑补思路:
- 从根结点出发,
- 如果左边还有没走的路,则继续走左边,走到尽头就往回走。
- 如果左边没路了,就往右边走。
- 如果两边都没有路了,就往上走。
4.2 二叉树的中序遍历
- 若二叉树为空,则什么也不做;
- 若二叉树非空:
先序遍历左子树
访问根节点(可对结点进行部分操作,比如输出结点的data值);
先序遍历右子树
//中序遍历
void InOrder(BiTree T)
{
if(T != NULL)
{
InOrder(T->lchild); //遍历左子树
vist(T); //可以进行部分操作
InOrder(T->rchild); //遍历右子树
}
}
脑补思路:
- 从根结点出发,
- 如果左边还有没走的路,则继续走左边,走到尽头就往回走。
- 如果左边没路了,就往右边走。
- 如果两边都没有路了,就往上走。
4.3 二叉树的后序遍历
- 若二叉树为空,则什么也不做;
- 若二叉树非空:
先序遍历左子树
先序遍历右子树
访问根节点(可对结点进行部分操作,比如输出结点的data值);
//后序遍历
void PostOrder(BiTree T)
{
if(T != NULL)
{
PostOrder(T->lchild); //遍历左子树
PostOrder(T->rchild); //遍历右子树
vist(T); //可以进行部分操作
}
}
4.4 二叉树的层序遍历
算法思想:
- 初始化一个辅助队列
- 根节点入队
- 若队列非空,则队头节点出队,访问该结点,并将其左、右孩子插入队尾(如果有的话)
//层序遍历
void LeveOrder(BiTree T)
{
LinkQueue Q; //定义链队的头结点
InitQueue(Q); //初始化链队
BiTree p;
EnQueue(Q,T); //将根结点入队
while(!IsEmpyty(Q)) //队列不空则进入循环
{
DeQueue(Q , p); //头结点出队
visit(p);
if(p->lchild != NULL)
EnQueue(Q, p->lchild); //左孩子入队
if(p->rchild != NULL)
EnQueue(Q, p->rchild); //右孩子入队
}
}