任务分析

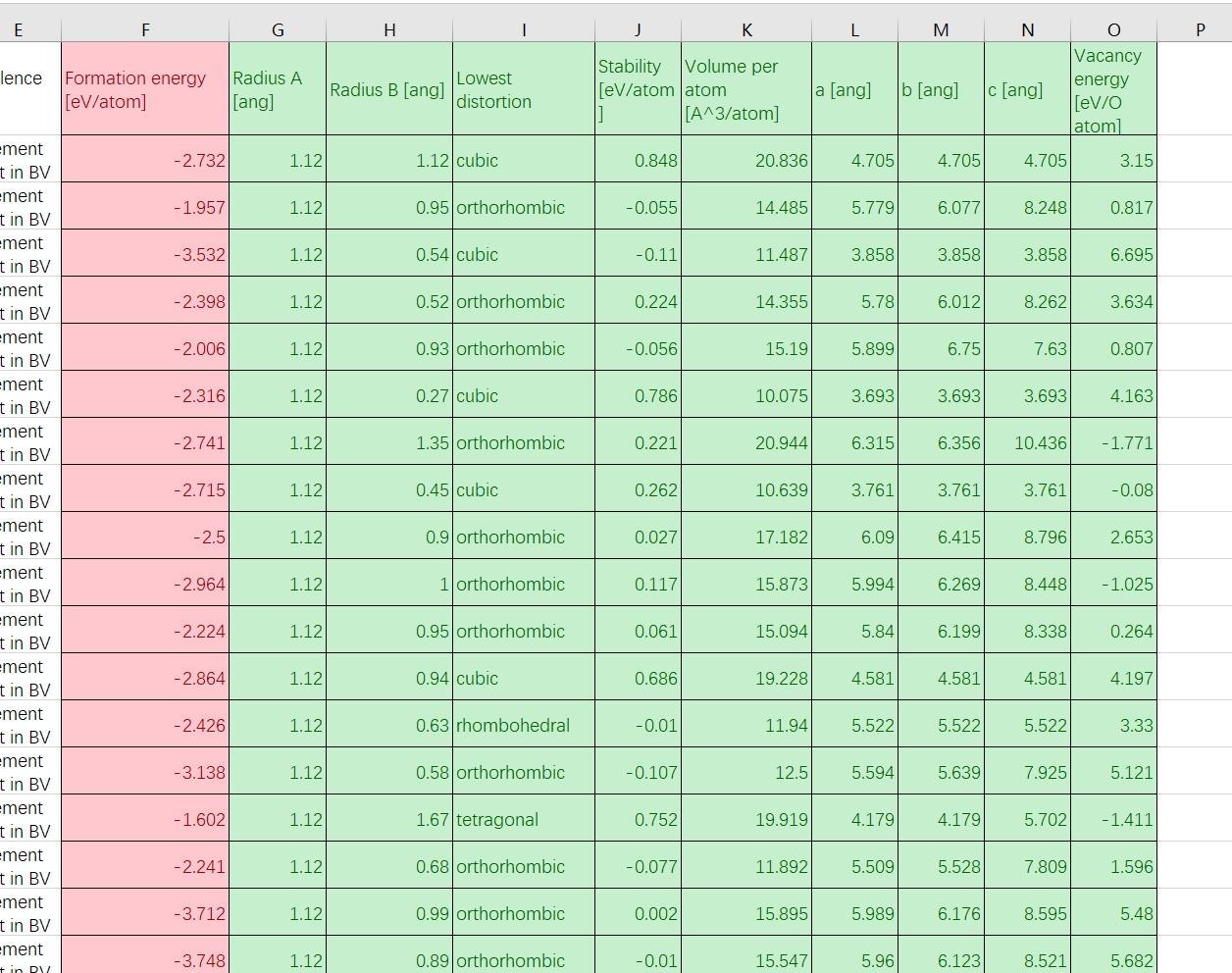
简单来说，就是一行就是一个样本，要用绿色的9个数值，预测出红色的那1个数值。

数据处理

在进行深度数学数据处理时，数据预处理是一个至关重要的步骤。它涉及到处理离散数值、缺失值以及不同范围的数据等问题。下面，我们将探讨如何高效地处理这些常见问题，并确保数据集为后续的分析和建模做好准备。

处理离散数值

离散数值通常指的是分类数据，这些数据可以是有序的（例如教育水平）或无序的（例如国籍）。在深度学习中，离散数值通常需要转换为一种更适合模型处理的格式。

独热编码（One-Hot Encoding）: 对于无序的分类变量，独热编码是一种常见的处理方法。它为每个类别创建一个新的布尔列，表示某个样本是否属于该类别。

标签编码（Label Encoding）: 对于有序的分类变量，可以使用标签编码，它将每个类别映射到一个整数值。这种方法保留了类别间的顺序关系。

嵌入（Embeddings）: 对于类别数量非常多的情况，可以使用嵌入层来学习一个更为紧凑的表示。

处理缺失值

缺失值处理是数据预处理中的一个重要方面。不同的处理方法可能会对模型的性能产生重大影响。

删除: 如果数据丢失不是很严重，可以考虑删除含有缺失值的行或列。但这可能会导致信息损失。

填充: 可以用某些统计值（如均值、中位数或众数）填充缺失值。对于连续变量，通常用均值或中位数；对于分类变量，可以用众数。

预测模型: 使用其他完整的特征来预测缺失值。例如，可以使用随机森林或K最近邻算法来预测缺失的数据。

使用缺失值: 某些算法可以直接处理缺失值，例如XGBoost。此外，可以将缺失值作为模型的一个特征。

处理不同范围的数据

当数据集中的特征在不同的范围内变化时，可能会导致模型性能下降，尤其是在使用基于距离的算法时。

标准化（Standardization）: 通过减去均值并除以标准差来转换数据，使得特征的均值为0，标准差为1。

归一化（Normalization）: 将特征缩放到给定的最小值和最大值之间，通常是0和1。

Robust Scaling: 使用中位数和四分位数范围来缩放特征，这种方法对异常值有更好的鲁棒性。

其他注意事项

异常值处理: 异常值可能是由于错误或偏差造成的。可以使用Z分数、IQR分数等方法检测并处理异常值。

特征工程: 考虑创建新的特征或转换现有特征，以更好地表示数据的潜在结构。

数据集的平衡: 在分类问题中，确保每个类别的样本数量大致相等，或者使用加权损失函数来解决类别不平衡问题。

时间序列数据: 如果数据是时间序列，需要考虑时间依赖性和季节性因素。

数据一致性: 确保所有数据都以一致的格式和单位进行表示。

通过以上的数据预处理方法，我们可以确保数据集为机器学习模型的训练和测试做好准备。这些步骤有助于提高模型的准确性、减少过拟合的风险，并提高模型的泛化能力。

我们的数据处理

独热编码、填充平均值、删除缺失数据过多（>3）的样本、标准化输入。

分析数据平稳性质，基本平稳，无需额外剔除工作。

模型

引入自注意力机制的神经网络模型：

class SelfAttention(nn.Module):
    def __init__(self, in_dim):
        super(SelfAttention, self).__init__()
        self.query = nn.Linear(in_dim, in_dim)
        self.key = nn.Linear(in_dim, in_dim)
        self.value = nn.Linear(in_dim, in_dim)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x):
        q = self.query(x)
        k = self.key(x)
        v = self.value(x)

        attention_weights = self.softmax(torch.matmul(q, k.transpose(-2, -1)) / (x.size(-1) ** 0.5))
        attention_output = torch.matmul(attention_weights, v)
        return attention_output


class AttentionModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(AttentionModel, self).__init__()
        self.fc0 = nn.Linear(input_dim, 1024)
        self.fc0_1 = nn.Linear(1024, 512)
        self.fc1 = nn.Linear(512, 256)
        self.fc2 = nn.Linear(256, 128)
        self.fc3 = nn.Linear(128, 64)
        self.fc4 = nn.Linear(64, output_dim)
        self.relu = nn.SELU()
        self.bn0 = nn.BatchNorm1d(1024)
        self.bn0_1 = nn.BatchNorm1d(512)
        self.bn1 = nn.BatchNorm1d(256)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(64)
        self.self_attention = SelfAttention(256)

    def forward(self, x):
        x = self.bn0(self.relu(self.fc0(x)))
        x = self.bn0_1(self.relu(self.fc0_1(x)))
        x = self.bn1(self.relu(self.fc1(x)))
        attention_output = self.self_attention(x)
        x = self.relu(attention_output + x)  # 残差连接后应用ReLU
        x = self.bn2(self.relu(self.fc2(x)))
        x = self.bn3(self.relu(self.fc3(x)))
        x = self.fc4(x)
        return x

    # 使用Xavier初始化或Kaiming初始化
    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                init.kaiming_uniform_(m.weight, mode='fan_in', nonlinearity='relu')
                if m.bias is not None:
                    init.constant_(m.bias, 0)

训练

MSE最低降低到0.2左右。

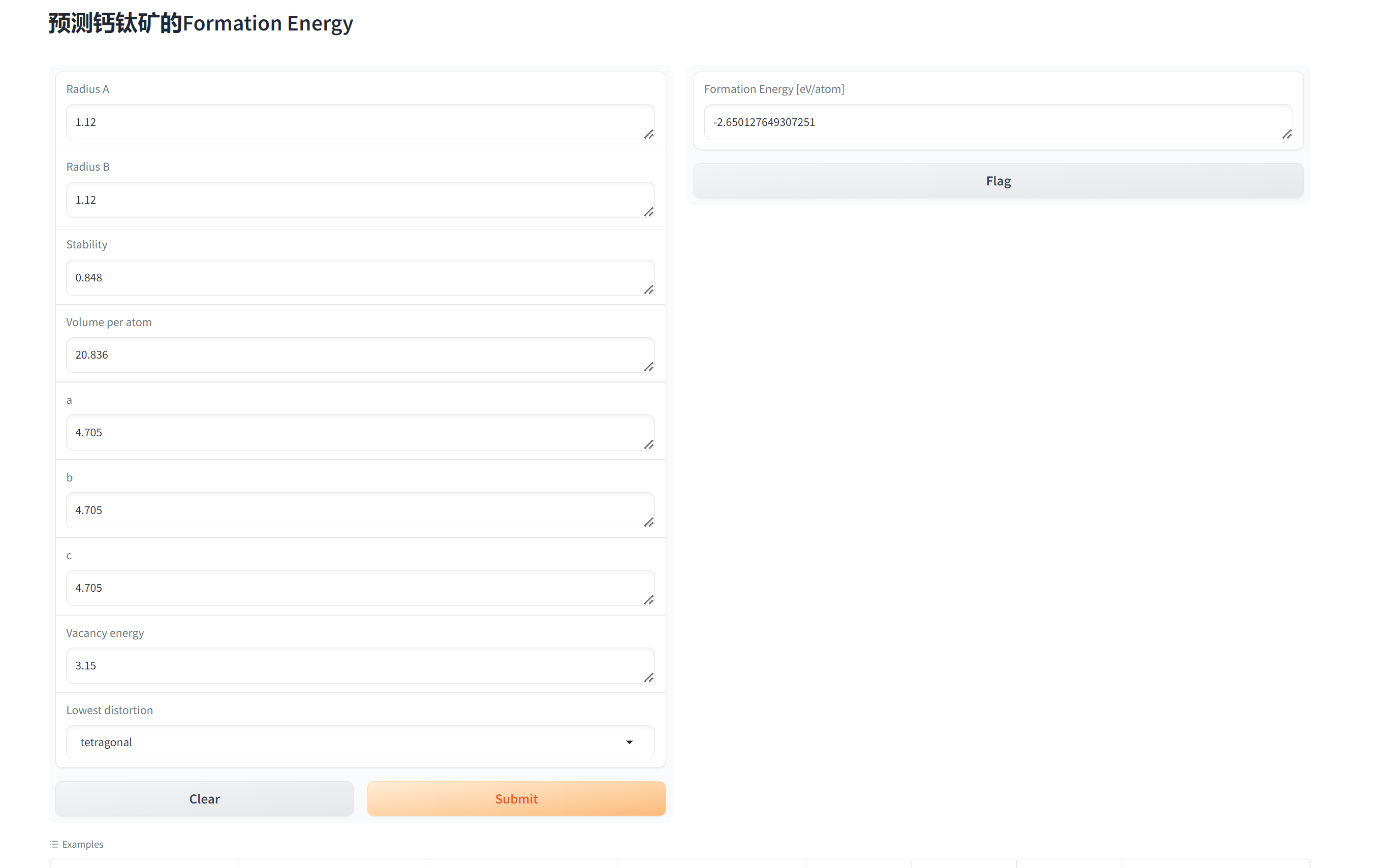
网页web

代码、指导

需要帮助请：

https://docs.qq.com/sheet/DUEdqZ2lmbmR6UVdU?tab=BB08J2