1.算法需求描述

现有随机生成的两个三角形A与B，在三角形A中存在Pa，使用算法计算出三角形B中对应的点Pb

2.python代码

import numpy as np  
  
# 计算三角形A的面积  
def area_triangle(vertices):  
    return 0.5 * np.abs(np.dot(vertices[0] - vertices[1], vertices[1] - vertices[2]))  
  
# 计算重心坐标  
def barycentric_coordinates(P, vertices):  
    v0 = vertices[1] - vertices[0]  
    v1 = vertices[2] - vertices[0]  
    v2 = P - vertices[0]  
      
    d00 = np.dot(v0, v0)  
    d01 = np.dot(v0, v1)  
    d11 = np.dot(v1, v1)  
    d20 = np.dot(v2, v0)  
    d21 = np.dot(v2, v1)  
      
    denom = d00 * d11 - d01 * d01  
    v = (d11 * d20 - d01 * d21) / denom  
    w = (d00 * d21 - d01 * d20) / denom  
    u = 1.0 - v - w  
      
    return np.array([u, v, w])  

def generate_random_triangle():
    # 随机生成三个点作为三角形的顶点
    vertices = np.random.rand(3, 2)  # 生成三个点，每个点有两个坐标值
    return vertices

def generate_random_point_in_triangle(triangle):
    # 生成两个随机数
    r1, r2 = np.random.rand(2)

    # 通过重心坐标法生成点
    sqrt_r1 = np.sqrt(r1)
    u = 1 - sqrt_r1
    v = r2 * sqrt_r1
    w = 1 - u - v

    # 计算点的坐标
    point = u * triangle[0] + v * triangle[1] + w * triangle[2]

    return point

import matplotlib.pyplot as plt

# 定义三角形的三个顶点坐标  
source_A = generate_random_triangle()
target_B = generate_random_triangle()

# 定义点P在三角形A内的坐标  
PA = generate_random_point_in_triangle(source_A) 

# 计算点P在三角形A中的重心坐标  
PA_coords = barycentric_coordinates(PA, source_A)  
  
# 使用重心坐标在三角形B中找到对应的点Pt  
PB = PA_coords[0] * target_B[0] + PA_coords[1] * target_B[1] + PA_coords[2] * target_B[2]  
  
print("Pt的坐标是:", PB)


# 绘制图形
plt.figure(figsize=(8, 6))

# 绘制A_arr构成的平面
plt.fill([point[0] for point in source_A], [point[1] for point in source_A], color='blue', alpha=0.2, label='A_arr Plane')

# 绘制B_arr中的点
plt.fill([point[0] for point in target_B], [point[1] for point in target_B], color='red', label='B_arr Points')

# 绘制source_P和target_P
plt.scatter(PA[0], PA[1], color='green', marker='o', label='Source Point')
plt.scatter(PB[0], PB[1], color='orange', marker='o', label='Target Point')

# 标记顶点顺序
for i, point in enumerate(source_A):
    plt.text(point[0], point[1], str(i + 1), fontsize=12, color='black', ha='right', va='bottom')
    
for i, point in enumerate(target_B):
    plt.text(point[0], point[1], str(i + 1), fontsize=12, color='black', ha='right', va='bottom')

plt.xlabel('X')
plt.ylabel('Y')
plt.title('Visualization of Points and Plane')
plt.legend()
plt.grid(True)
plt.show()

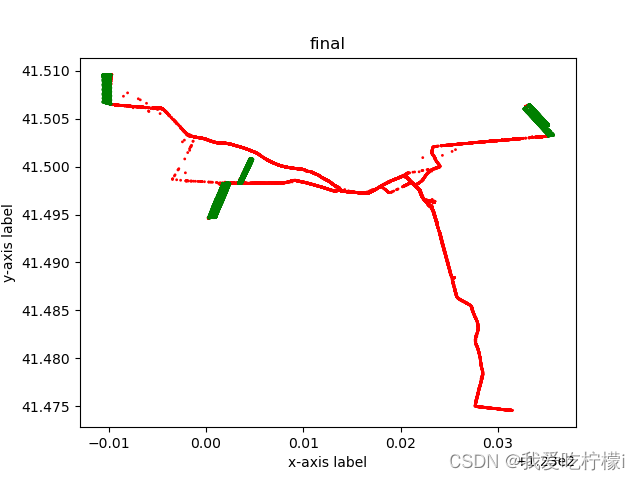
3.计算结果