leetcode刷题（javaScript）——BFS广度优先遍历相关场景题总结

广度优先搜索（BFS）在JavaScript编程中有许多实际应用场景，特别是在解决图、树等数据结构相关问题时非常常见。在JavaScript中，可以使用队列来实现广度优先搜索算法。通过将起始节点加入队列，然后迭代地将节点的邻居节点加入队列，直到队列为空为止。这样可以逐层地遍历图或树结构，找到目标节点或满足条件的节点。在实际编程中，需要注意避免重复访问节点、处理环路等问题，确保算法的正确性和效率。以下是一些JavaScript中广度优先搜索的常见使用场景：

图的遍历：在图算法中，广度优先搜索可以用来遍历图中的节点，查找从一个节点到另一个节点的最短路径。
树的层次遍历：在处理树结构时，广度优先搜索可以用来按照层次遍历树的节点，通常使用队列来实现。
迷宫问题：在解决迷宫问题时，可以使用广度优先搜索来找到从起点到终点的最短路径。
社交网络分析：在社交网络中，可以使用广度优先搜索来查找两个人之间的最短路径，或者查找某人的朋友圈。
游戏中的路径查找：在游戏开发中，广度优先搜索可以用来查找玩家角色到达目的地的最短路径。
最小生成树：在图论中，广度优先搜索可以用来生成最小生成树，如Prim算法和Kruskal算法。

某些情况下既可以用DFS又可以用BFS怎么选择呢？

如果问题需要找到最短路径或最短距离，通常使用 BFS，因为 BFS 会逐层遍历，当找到目标时，路径一定是最短的。
如果问题需要找到所有解，通常使用 DFS，因为 DFS 会一直往深处搜索，能够找到所有可能的解。
如果问题的搜索空间较大，可能会导致 DFS 的递归栈很深，可能会导致栈溢出，这时候可以考虑使用 BFS。

上题：可以按照博主的列的题目顺序依次练习，二叉树的简单，图论的难，但是做题技巧比较固定

二叉树相关

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

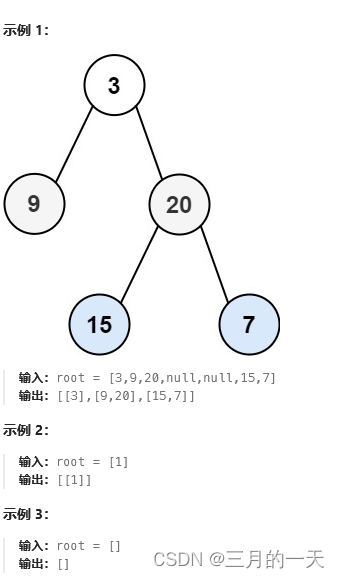
思路：采用广度优先搜索（BFS）的思想，可以按照层次遍历的顺序逐层访问节点，保证了每一层的节点都被访问到。使用队列来存储待遍历的节点，保证了按照节点的入队顺序依次出队，实现了层次遍历的效果。通过队列的先入先出特性，可以确保在每一层节点遍历时，先访问左孩子再访问右孩子，符合层次遍历的要求。

具体步骤如下：

首先，判断根节点是否存在，若不存在则返回空数组。
使用队列来存储待遍历的节点，保证按照层次遍历的顺序访问节点。
进入循环，只要队列中还有节点未被遍历，就继续循环。
在每一轮循环中，记录当前层节点的个数，以便控制循环次数。
在内层循环中，依次将当前层节点出队，并将节点值存入临时数组中。
对于每个出队的节点，如果存在左孩子，则将左孩子入队；如果存在右孩子，则将右孩子入队。
将当前层的节点值数组存入结果数组中。
最终返回结果数组，即每一层节点值的二维数组。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    //处理边界
    if(!root) return [];
    let queue = [root];//用队存储未遍历节点，左节点先入队
    let res=[];//存储遍历结果
    while(queue.length){//只要有未遍历左右子树节点存在，继续
        let len = queue.length;//len当前层节点的个数，for循环结束的边界
        let temp = [];
        for(let i =0; i<len; i++){
            const node = queue.shift();//按照入队的顺序，先入先出，左节点先出
            temp.push(node.val);
            node.left && queue.push(node.left);//如果出队的节点有左孩子，左子树先入队
            node.right && queue.push(node.right);//右子树后入队
        }
        res.push(temp);//将当前层遍历结果push到结果数组中
    }
    return res;
};

103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

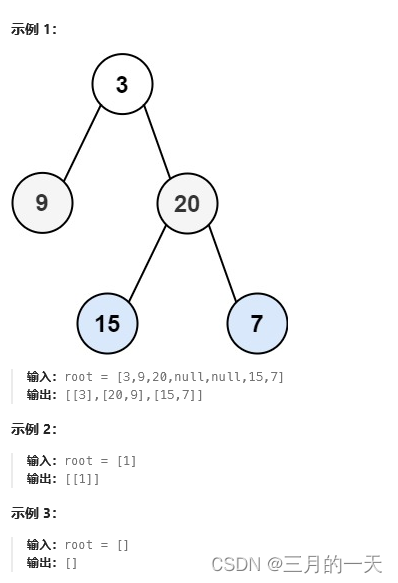
思路：在上一题的基础上加上isReverse的标识。因为每层的遍历结果还是存储在temp数组中。只要直到当前需要翻转，那么就处理temp数组：在插入时翻转，或者插入后reverse。都行，这里采用插入时翻转。push进res数组后，改变isReverse的状态。true->false false->true

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var zigzagLevelOrder = function (root) {
    //边界条件
    if (!root) return [];
    let queue = [root];//队列存储每层未遍历的节点
    let res = [];//存储结果数组
    let isReverse = false;//当前是否需要翻转，初始化false不翻转
    while (queue.length) {
        let len = queue.length;//当前遍历层的节点个数
        let temp = [];//当前层遍历结果
        for (let i = 0; i < len; i++) {//对当前层所有未遍历的节点
            const node = queue.shift();//将节点shift出去
            if (isReverse) {//判断是否需要翻转，需要翻转的将左节点靠右插入
                temp.unshift(node.val);
            } else {
                temp.push(node.val);//不需要翻转，靠左插入
            }
            node.left && queue.push(node.left);//插入左右节点，先插座节点
            node.right && queue.push(node.right);
        }
        res.push(temp);
        isReverse = !isReverse;//改变下一层翻转标识
    }
    return res;
};

107. 二叉树的层序遍历 II

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

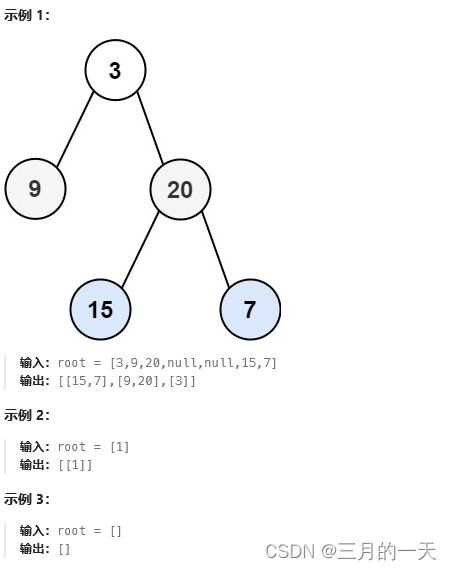
思路：可以按正常层序遍历结束后reverse，也可以在插入res数组时不用push，用unshift，从数组左边插入。这样就能保证先入数组的在最后面。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrderBottom = function (root) {
    //处理边界
    if (!root) return [];
    let queue = [root];
    let res = [];
    while (queue.length) {
        let len = queue.length;
        let temp = [];
        for (let i = 0; i < len; i++) {
            const node = queue.shift();
            temp.push(node.val);
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        res.unshift(temp);//改变层插入顺序，从数组的左边插入，最先插入的在右边
    }
    return res;
};

112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。叶子节点 是指没有子节点的节点。

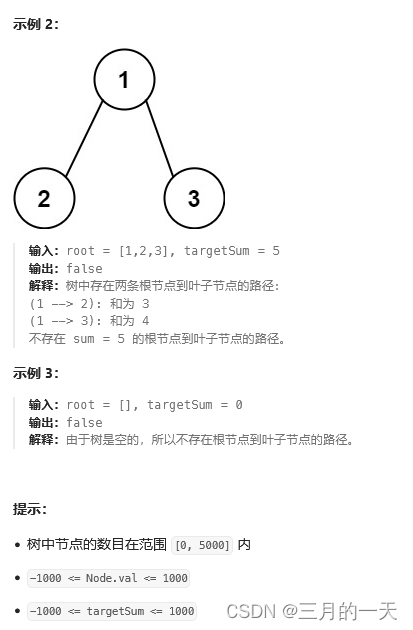
思路：这道题可以递归或者dfs实现。在本专题中就用BFS实现。从前面的题来看，BFS就是通过层次遍历的思想来解决二叉树的具体问题。在解决这种路径上信息的问题，有个做题技巧，就是队列的元素除了存放节点，还可以存放节点的路径信息。通常用一个数组表示：[node,node.val,path等]根据需求扩展信息。当然也可以用对象，对象还要定义key，这里用解构取数据，根据解构定义的合适的变量名也能见名知其意。

本题中定义节点入队的信息[node,curSum+node.val]

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function (root, targetSum) {
    //处理边界
    if (!root) return false;
    let queue = [[root, root.val]];//队列存储待遍历的节点，以及访问当当前经过的节点值
    while (queue.length) {
        let len = queue.length;
        for (let i = 0; i < len; i++) {//遍历每层
            const [node, curSum] = queue.shift();//通过解构得到当前层遍历的某个节点和到大该节点的路径信息
            if (!node.left && !node.right && curSum === targetSum) {//如果是叶子节点并且当前sum等于targetSum返回true
                return true;
            }
            node.left && queue.push([node.left, curSum + node.left.val]);//依次push左右子树，注意push的是一个数组，第一个信息是节点，第二个是节点遍历的路径和
            node.right && queue.push([node.right, curSum + node.right.val]);
        }
    }
    return false;
};

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。初始状态下，所有 next 指针都被设置为 NULL。

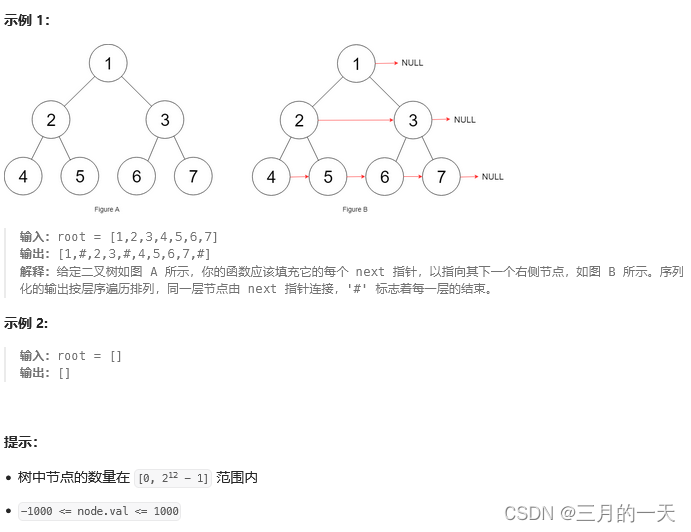
思路：这道题的题目真的一言难尽，给的示例干嘛给输出加什么#号，导致我以为要按照那个格式输出。。其实就是返回一个新的二叉树，根据每层节点情况添加一个next指针。

ok，就用BFS，在同层节点也就是for循环的时候处理一下就好了，当前节点node，他的next指向他的右边兄弟节点=队列的第一个元素queue[0]

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function (root) {
    if (!root) return null;
    let queue = [root];
    while (queue.length) {
        const len = queue.length;
        for (let i = 0; i < len; i++) {
            const node = queue.shift();
            if (i !== len - 1) {//非当前层最后一个节点
                node.next = queue[0];//链接next节点，从当前层未访问的第一个节点比较，注意不能shift
            }
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return root;//返回root节点，生成了新的加入了next指针的节点
};

623. 在二叉树中增加一行

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。注意，根节点 root 位于深度 1 。

加法规则如下:

给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
cur 原来的左子树应该是新的左子树根的左子树。
cur 原来的右子树应该是新的右子树根的右子树。
如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

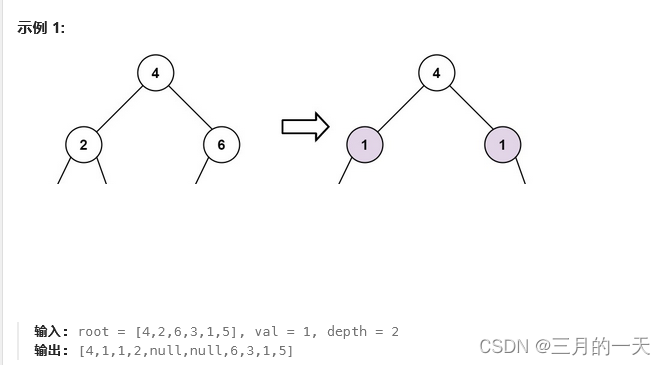
思想：还是利用层次遍历，找到当前层节点信息，如果当前层的高度+1等于depth。那么给当前层的所有节点依次加入左右子节点。这时候要保证新加入的节点不破坏原有指针的连接关系。要先创建左右新的节点，然后让新的左节点的左指针指向原来节点的左孩子；让新的右节点的右指针指向原来节点的右孩子。这样将原来的节点串起来，之后将新的左右节点赋给该遍历的节点。这样新的节点关系确立。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @param {number} depth
 * @return {TreeNode}
 */
var addOneRow = function (root, val, depth) {
    //处理边界
    if (depth == 1) {
        let node = new TreeNode(val, root);
        return node;
    }
    let queue = [root];//队列
    let level = 1;//设置当前层高
    while (queue.length) {
        const len = queue.length;
        for (let i = 0; i < len; i++) {//遍历当前层
            const node = queue.shift();//拿到节点
            if (level + 1 == depth) {//当前层+1等于depth，需要再当前层下方增加节点
                let left = new TreeNode(val, node.left);//创建左节点，左节点的左孩子等于node.left
                let right = new TreeNode(val, null, node.right);//创建右节点，右节点的右孩子等于node.right
                node.left = left;//将的左节点复制给node
                node.right = right;//将新的右节点复制给node
            } else {//正常层次遍历
                node.left && queue.push(node.left);
                node.right && queue.push(node.right);
            }
        }
        //for循环结束，如果当前层+1等于depth返回新的root
        if (level + 1 === depth) {
            return root;
        }
        level++;
    }
};

993. 二叉树的堂兄弟节点

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

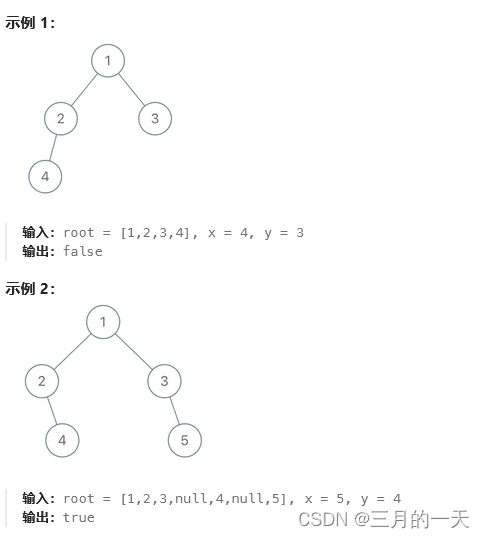
思路：这题标记为简单题，中等题号吗，简单题不用思考的。这题可以用dfs找到节点并记住节点的深度，节点的父亲。或者使用bfs+队列，记住节点和节点的父亲。在同层节点里判断是否同时存在x,y，并且x和y的父亲不是同一个。OK，思路清楚，开干。

依然使用数组保存节点的两个信息，当前节点，当前节点父亲节点。这样在比较时就能比较值和父节点了。使用解构方式定义变量，能够见名知其意。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} x
 * @param {number} y
 * @return {boolean}
 */
var isCousins = function (root, x, y) {
    if (!root) return false;
    let queue = [[root, null]];//借助队列，用数组形式，节点存两个信息，一个是当前节点信息，一个是父节点信息。
    while (queue.length) {
        let len = queue.length;
        let findX = [];//每层重新找findX、findY
        let findY = [];
        for (let i = 0; i < len; i++) {//遍历未遍历的节点
            const [node, parent] = queue.shift();//从当前层移出一个节点
            if (node.val == x) {//找x和y
                findX = [node, parent];
            } else if (node.val == y) {
                findY = [node, parent];
            } else {//没找到继续push
                node.left && queue.push([node.left, node]);
                node.right && queue.push([node.right, node]);
            }
        }
        //当前层遍历后看有没有找到x和y，并且看x和y的父节点是否不一样
        if (findX.length && findY.length && findX[1] != findY[1]) {
            return true;
        }
    }
    return false;
};

1448. 统计二叉树中好节点的数目

给你一棵根为 root 的二叉树，请你返回二叉树中好节点的数目。

「好节点」X 定义为：从根到该节点 X 所经过的节点中，没有任何节点的值大于 X 的值。

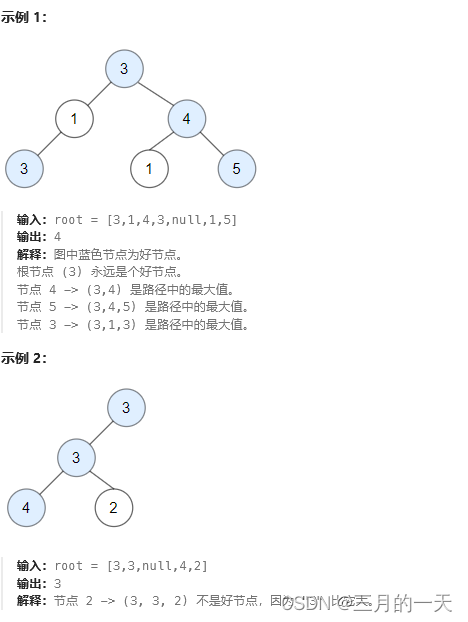
思路：使用BFS+队列，队列的每个元素用数组表示，数组第一个是节点，第二个是到达该节点路径中节点的最大值。只要比较当前节点是否大于最大值即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var goodNodes = function (root) {
    let max = root.val;//初始时最大节点为根
    let queue = [[root, max]];//队列定义，节点和到达该节点路径上最大的值、
    let count = 0;//好节点个数
    while (queue.length) {
        let len = queue.length;
        for (let i = 0; i < len; i++) {
            const [node, preMax] = queue.shift();
            if (node.val >= preMax) {
                count++;
            }
            max = Math.max(preMax,node.val);//更新当前节点的max值
            node.left && queue.push([node.left, max]);
            node.right && queue.push([node.right, max]);
        }
    }
    return count;
};

矩阵相关

在图里应用BFS可能有些难以理解，不过都有一种套路。在二叉树里，节点向下走，可以用指针，找当前节点的左孩子或右孩子。在图里怎么继续向下走呢，其实要定义行走的方向，通常当前的位置是[x,y]定义行走的方向比如[dx,dy]=[1,0]，那么当前位置加上这个方向=[x+1,y]，也就是向右走了一步，通过定义的方向决定下一步走的范围。

图的BFS就像是病毒扩散，每一次只向四周扩散一步，所有的节点都参与扩散，直到充满整个图，或者覆盖目标节点。当然BFS还是结合一个数据结构进行存储，通常选用队列，也可以用别的，选择队列在逻辑上是按入队的顺序进行遍历的。那队列里入队的信息简单的可以只有当前的节点左边，复杂的可能附加别的路径等额外信息。

对每个方向都尽可能尝试是否可以走，并且注意行走的新的x和y要符合逻辑。以下模板可能具有参考性。
  const directions = [
    [0, 1], //向下走一步，
    [0, -1], //向上走一步
    [1, 0], //向右走一步
    [-1, 0], //向左走一步
  ];

  const queue = [start]; // 初始化队列
  while (queue.length > 0) {
    const [x, y] = queue.shift(); // 通过解构 从队列中取出当前位置
    //可终止的逻辑

    //广度优先搜索，遍历当前位置的四个方向，各走一步得到一组新的结果
    for (const [dx, dy] of directions) {
      // 遍历四个方向
      const newX = x + dx; // 计算新位置的横坐标
      const newY = y + dy; // 计算新位置的纵坐标

      // 判断新位置是否在迷宫范围内、是否为可通行、是否已经访问过
      if (
        newX >= 0 &&
        newX < rows &&
        newY >= 0 &&
        newY < cols && 具体条件
      ) {
        //处理具体问题
        queue.push([newX, newY]); // 将新位置加入队列
      }
    }
  }

}

在做下面一道题之前可以看我前面写的一个迷宫问题的博客，这个简单一些
javaScript——BFS结合队列求迷宫最短路径-CSDN博客

994. 腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

思路：注意所有腐烂的橘子都可以同时向四周进行腐烂。

用队列存储所有未办遍历的腐烂的节点，然后对每个腐烂的节点，尝试从四个方向各走一步，将新的腐烂的节点加入队列中，重复操作，直到过程中没有新鲜的橘子为止。

注意初始化时要手动找到第一波腐烂的橘子。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function (grid) {
    //利用BFS存储待遍历的坏橘子
    let queue = [];
    const rows = grid.length;
    const cols = grid[0].length;
    //初始化腐烂的橘子
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] === 2) {
                queue.push([i, j]);//获取腐烂橘子坐标push入队列
            }
        }
    }
    //定义四个方向
    const directions = [
        [0, 1], [0, -1], [1, 0], [-1, 0]
    ];
    let min = 0;
    while (queue.length) {
        let len = queue.length;
        if (!hasFresh(grid, rows, cols)) {//过程中如果已经没有腐烂的橘子，返回min
            return min;
        }
        for (let i = 0; i < len; i++) {//遍历当前未访问的坏橘子
            const [X, Y] = queue.shift();
            for (let [dx, dy] of directions) {//每个方向都尝试走一步，如果碰到好橘子，感染它
                const newX = X + dx;
                const newY = Y + dy;
                if (newX >= 0 && newX < rows && newY >= 0 && newY < cols && grid[newX][newY] == 1) {//找到好橘子了，
                    grid[newX][newY] = 2;//杀死它
                    queue.push([newX, newY]);//等会遍历它
                }
            }
        }
        min++;
    }
    return hasFresh(grid, rows, cols) ? -1 : min;
};
//判断网格中是否还有好橘子
function hasFresh(grid, rows, cols) {
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] === 1) {
                return true;
            }
        }
    }
    return false;
}

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

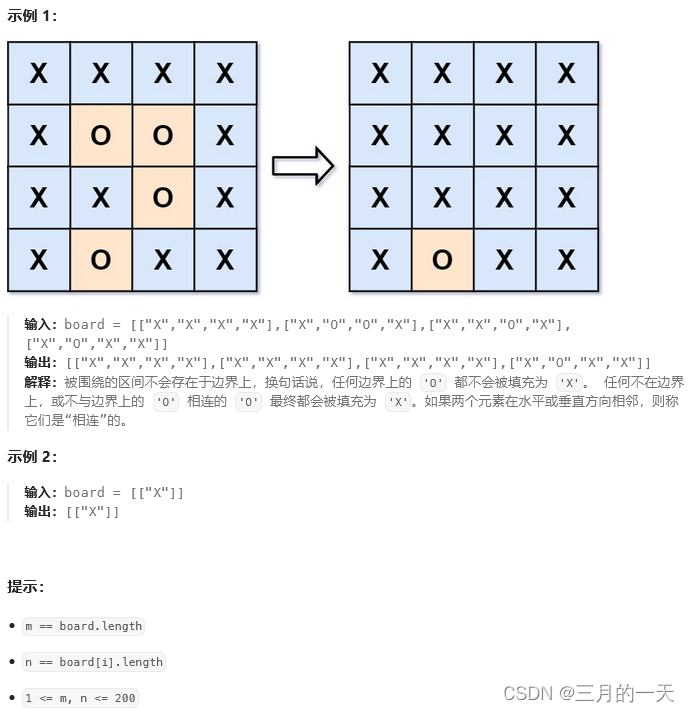
思路：由于题目说了，与边界O相邻的元素不算被X包围。所以O被分为两类，一类是经过相邻的O元素可以到达边界O的，另一种是无法到达边界O的。那么可以将边界上的O理解为病毒，将边界O设置为特殊值，比如#。让其向内扩散。扩散时找到了相邻是O的节点，将其加入，并赋值#。剩下的没改变的O就是被包围的O啦。

具体步骤如下：

遍历矩阵的四条边，将边界上的 'O' 及其坐标加入队列，并改为#。

对队列中的每个坐标进行BFS搜索：出队一个坐标，检查该坐标的上、下、左、右四个相邻坐标，是否是非边界合理值，并且值是否为 'O'。如果是则将其坐标加入队列，并设置为#。

最后，遍历整个矩阵，先将剩余的 'O' 修改为 'X'，在将特殊字符'#'恢复为'O'。

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var solve = function (board) {

    if (!board || !board.length) return;
    const rows = board.length;
    const cols = board[0].length;
    const queue = [];
    const directions = [
        [1, 0], [-1, 0], [0, 1], [0, -1]
    ];
    //将边界上的'O'及其非边界为'O'坐标加入队列
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if ((i == 0 || i == rows - 1 || j == 0 || j == cols - 1) && board[i][j] === 'O') {//优雅边界判断
                queue.push(([i, j]));
                board[i][j] = '#';
            }
        }
    }
    //将边界能连通的节点O都变成#
    while (queue.length) {
        const [X, Y] = queue.shift();
        for (let [dx, dy] of directions) {
            const newX = X + dx;
            const newY = Y + dy;
            if (newX >= 1 && newX < rows - 1 && newY >= 1 && newY < cols - 1 && board[newX][newY] === 'O') {
                queue.push([newX, newY]);
                board[newX][newY] = '#';
            }
        }
    }
    //剩下的O是被X包围的
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (board[i][j] === 'O') {
                board[i][j] = 'X';
            } else if (board[i][j] === '#') {
                board[i][j] = 'O';
            }
        }
    }
    return board;
};

题型思路总结

思路：如果题型是矩阵，然后可以通过找到一批节点，通过扩散的思维，遍历到其他的节点。那么就考虑BFS。

用数组将病毒节点先存起来。通过定义的四个方向，每个方向都尝试走一步，干能否感染邻居节点。将可以感染的邻居节点加入到这个数组中。然后进行逻辑处理。

1.获取矩阵的行列+定义四个方向

    const rows = matrix.length;
    const cols = matrix[0].length;
    const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];

2. 找到第一波病毒节点（源病毒）

示例一：腐烂的橘子

    //初始化腐烂的橘子
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] === 2) {
                queue.push([i, j]);//获取腐烂橘子坐标push入队列
            }
        }
    }

示例二：边界上的O

    //将边界上的'O'及其非边界为'O'坐标加入队列
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if ((i == 0 || i == rows - 1 || j == 0 || j == cols - 1) && board[i][j] === 'O') {//优雅边界判断
                queue.push(([i, j]));
                board[i][j] = '#';
            }
        }
    }

3.循环处理数组中未遍历的病毒+每个方向扩散一次

示例一：腐烂的橘子，当前腐烂的橘子向四周各走一步，感染其他橘子

while (queue.length) {
        let len = queue.length;
        if (!hasFresh(grid, rows, cols)) {//过程中如果已经没有腐烂的橘子，返回min
            return min;
        }
        for (let i = 0; i < len; i++) {//遍历当前未访问的坏橘子
            const [X, Y] = queue.shift();
            for (let [dx, dy] of directions) {//每个方向都尝试走一步，如果碰到好橘子，感染它
                const newX = X + dx;
                const newY = Y + dy;
                if (newX >= 0 && newX < rows && newY >= 0 && newY < cols && grid[newX][newY] == 1) {//找到好橘子了，
                    grid[newX][newY] = 2;//杀死它
                    queue.push([newX, newY]);//等会遍历它
                }
            }
        }
        min++;
    }

示例二：扩散的O，将能与边界O相接的O都变为#

    //将边界能连通的节点O都变成#
    while (queue.length) {
        const [X, Y] = queue.shift();
        for (let [dx, dy] of directions) {
            const newX = X + dx;
            const newY = Y + dy;
            if (newX >= 1 && newX < rows - 1 && newY >= 1 && newY < cols - 1 && board[newX][newY] === 'O') {
                queue.push([newX, newY]);
                board[newX][newY] = '#';
            }
        }
    }