【复杂网络建模】——建模工具Matlab入门

一、认识MATLAB

二、认识工具箱

三、基本操作和函数

3.1 算术操作符

3.2 数学函数

3.3 矩阵操作

3.4 索引和切片

3.5 逻辑操作

3.6 控制流程

3.7 数据输入输出

四、变量和数据类型

4.1 数值类型

4.2 整型

4.3 复数

4.4 字符串

4.5 逻辑类型

4.6 结构体（Structures）

4.7 单元格数组（Cell Arrays）

4.8 表格（Tables）

4.9 时间序列和日期时间

4.10 函数句柄

五、数组和矩阵运算

5.1 创建数组和矩阵

5.2 数组和矩阵的运算

5.3 数组和矩阵的索引

5.4 多维数组

一、认识MATLAB

MATLAB的产生是与数学计算紧密联系在一起的。1980年，美国新墨西哥州大学计算机系主任Cleve Moler在给学生讲授线性代数课程时，发现学生在高级语言编程上花费很多时间，于是着手编写供学生使用的Fortran子程序库接口程序，取名为MATLAB（即Matrix Laboratory的前三个字母的组合，意为“矩阵实验室”）。

二、认识工具箱

MATLAB拥有一个专用的家族产品，用于解决不同领域的问题，称之为工具箱（Toolbox）。工具箱用于MATLAB的计算和画图，通常是M文件和高级MATLAB语言集合，使用户可以方便地修改函数和源代码，或增加新的函数。用户还可以结合不同的工具箱中的技术来设计针对某个问题的解决方案。MATLAB每年都会完善或新增一些工具箱，因此，在一般情况下，工具箱的列表不是固定不变的。有关MATLAB工具箱的最新信息可以在常见工具箱中看到。常见的工具箱：

AI、数据科学和统计学

Deep Learning Toolbox
Statistics and Machine Learning Toolbox
Curve Fitting Toolbox
Text Analytics Toolbox

数学和优化

Optimization Toolbox
Global Optimization Toolbox
Symbolic Math Toolbox
Mapping Toolbox
Partial Differential Equation Toolbox

三、基本操作和函数

3.1 算术操作符

+：加法
-：减法
*：乘法
/：除法
^：幂运算
.*、./、.^：数组元素的乘法、除法和幂运算

% 加法
result = 3 + 5;

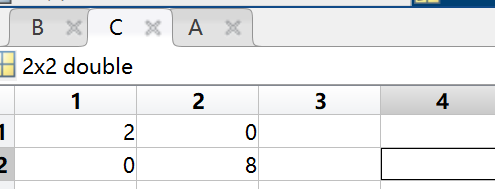
% 矩阵元素乘法
A = [1 2; 3 4];
B = [2 0; 0 2];
C = A .* B;

3.2 数学函数

MATLAB提供了大量的内置数学函数，用于处理各种数学运算：

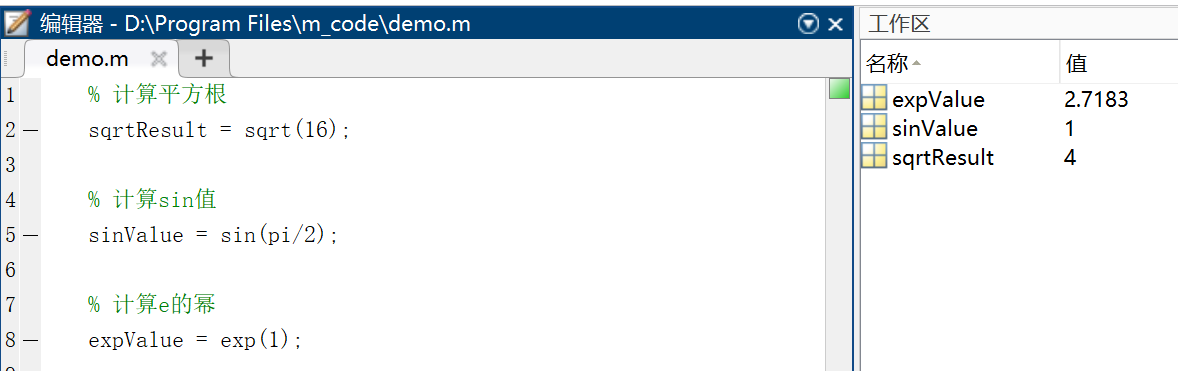
sqrt(x)：计算x的平方根
abs(x)：计算x的绝对值
sin(x)、cos(x)、tan(x)：三角函数
exp(x)：计算e的x次幂
log(x)、log10(x)：自然对数和以10为底的对数
round(x)、floor(x)、ceil(x)：对x进行四舍五入、向下取整、向上取整

% 计算平方根
sqrtResult = sqrt(16);

% 计算sin值
sinValue = sin(pi/2);

% 计算e的幂
expValue = exp(1);

3.3 矩阵操作

MATLAB是矩阵实验室（Matrix Laboratory）的缩写，因此矩阵操作是它的强项：

[1 2 3]：创建行向量
[1; 2; 3]：创建列向量
A = [1 2 3; 4 5 6; 7 8 9]：创建矩阵
A'：矩阵转置
inv(A)：矩阵A的逆
det(A)：矩阵A的行列式
eig(A)：矩阵A的特征值和特征向量

% 创建矩阵
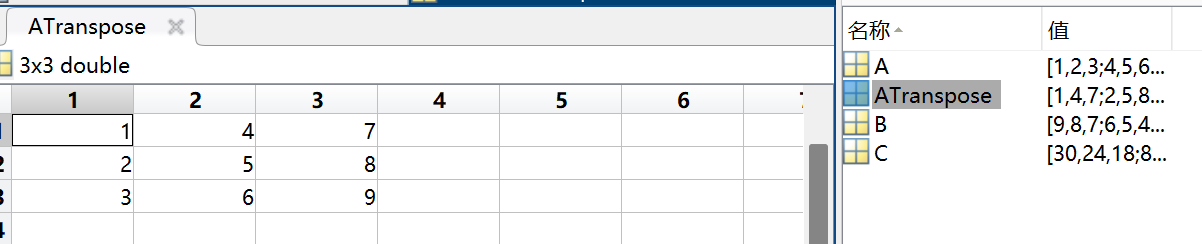
A = [1 2 3; 4 5 6; 7 8 9];

% 矩阵转置
ATranspose = A';

% 矩阵乘法
B = [9 8 7; 6 5 4; 3 2 1];
C = A * B;

3.4 索引和切片

A(1,2)：访问矩阵A中第一行第二列的元素
A(:,1)：访问A的第一列所有元素
A(1:3)：访问A中前三个元素（如果A是向量）

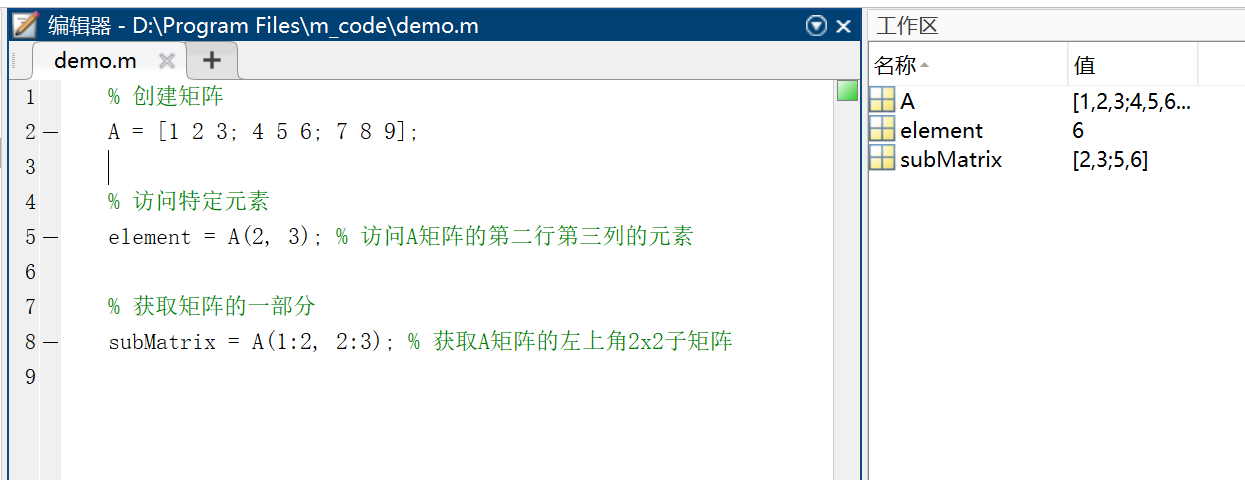
% 访问特定元素
element = A(2, 3); % 访问A矩阵的第二行第三列的元素

% 获取矩阵的一部分
subMatrix = A(1:2, 2:3); % 获取A矩阵的左上角2x2子矩阵

3.5 逻辑操作

==、~=：等于、不等于
<、>、<=、>=：小于、大于、小于等于、大于等于
&&、||、~：逻辑与、逻辑或、逻辑非

3.6 控制流程

if、else、elseif：条件语句
for：循环语句，用于重复执行代码块固定次数
while：当给定条件为真时，重复执行代码块

3.7 数据输入输出

load、save：加载和保存数据文件
fprintf、sprintf：格式化数据输出
input：从用户接收输入

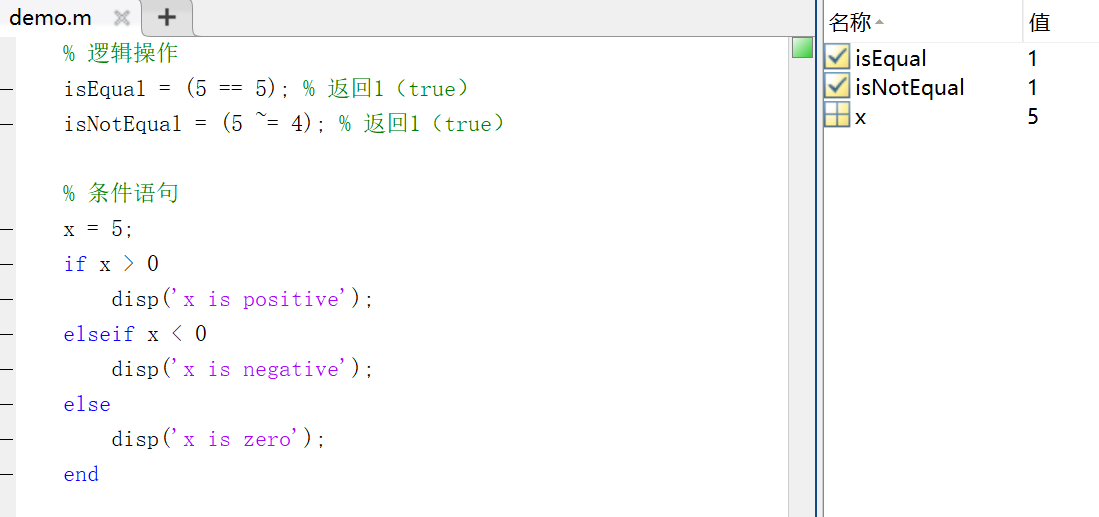
% 逻辑操作
isEqual = (5 == 5); % 返回1（true）
isNotEqual = (5 ~= 4); % 返回1（true）

% 条件语句
x = 5;
if x > 0
    disp('x is positive');
elseif x < 0
    disp('x is negative');
else
    disp('x is zero');
end

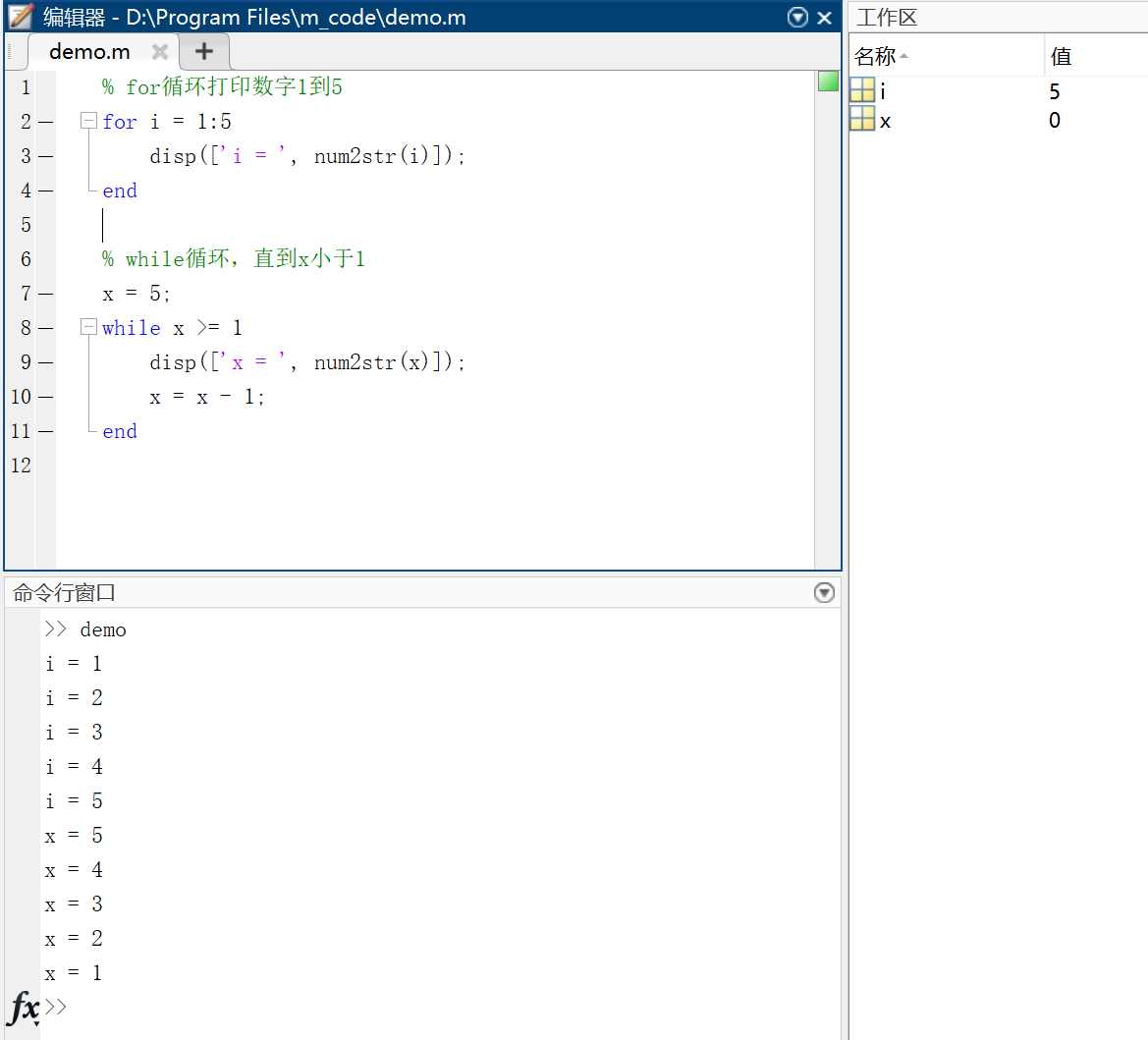
% for循环打印数字1到5
for i = 1:5
    disp(['i = ', num2str(i)]);
end

% while循环，直到x小于1
x = 5;
while x >= 1
    disp(['x = ', num2str(x)]);
    x = x - 1;
end

假设我们有一个名为data.txt的文本文件，内容为几行数字。这里需要新建一个data.txt文件。

% 读取文件
data = load('data.txt');

% 保存变量到文件
save('newData.txt', 'data');

四、变量和数据类型

在MATLAB中，变量用于存储数据，而数据类型决定了这些数据可以如何被处理和存储。了解MATLAB的基本变量和数据类型是进行有效编程的关键。以下是MATLAB中一些主要的变量类型和数据类型：

4.1 数值类型

双精度（Double）：MATLAB中的默认数据类型。用于表示带有小数点的数值，例如 x = 3.1415。
单精度（Single）：用于存储单精度浮点数，可以通过 single 函数创建，例如 y = single(3.1415)。

4.2 整型

MATLAB支持多种整型，包括 int8、int16、int32、int64 及其无符号版本 uint8、uint16、uint32、uint64。整型用于存储整数值，例如 z = int32(10)。

4.3 复数

MATLAB可以直接处理复数，例如 z = 3 + 4i。

4.4 字符串

MATLAB中的字符串是字符数组，用于表示文本。在MATLAB R2016b及以后的版本中，可以使用双引号创建字符串，例如 str = "Hello, MATLAB!"。

4.5 逻辑类型

表示真（true）或假（false）的值，用于条件表达式和逻辑运算，例如 flag = true。

4.6 结构体（Structures）

结构体是一种数据结构，可以包含不同类型的数据。例如，创建一个包含学生信息的结构体：student.name = "John Doe"; student.age = 21; student.grade = "A";。

4.7 单元格数组（Cell Arrays）

单元格数组是一种特殊的数组，可以存储不同类型和大小的数据。通过花括号创建和索引，例如 C = {'Hello', [1, 2, 3], 3.14};。

4.8 表格（Tables）

表格用于存储列变量形式的异质数据，是数据分析和处理的强大工具。例如，创建一个表格存储不同学生的信息：T = table({'John'; 'Jane'}, [21; 22], 'VariableNames', {'Name', 'Age'});。

4.9 时间序列和日期时间

MATLAB提供了日期和时间的数据类型，如 datetime，用于处理日期和时间数据，例如 dt = datetime('now') 获取当前时间。

4.10 函数句柄

函数句柄允许将函数作为参数传递给其他函数，例如 f = @sin; result = f(pi/2);。

五、数组和矩阵运算

在MATLAB中，数组和矩阵是核心的数据结构，几乎所有的操作和函数都是围绕它们设计的。MATLAB（Matrix Laboratory的缩写）特别适合于处理矩阵和线性代数运算。我们需要掌握数组的基本操作，包括索引、切片、维度操作等，以及矩阵的算数和线性代数运算。

数组：在MATLAB中，数组可以是一维的（向量），二维的（矩阵），或者多维的。数组中的所有元素必须是相同的数据类型。
矩阵：矩阵是二维数组的一个特例，其中的元素可以进行数学上的矩阵运算。矩阵运算在MATLAB中是非常高效的。

5.1 创建数组和矩阵

创建数组和矩阵非常直接。例如：

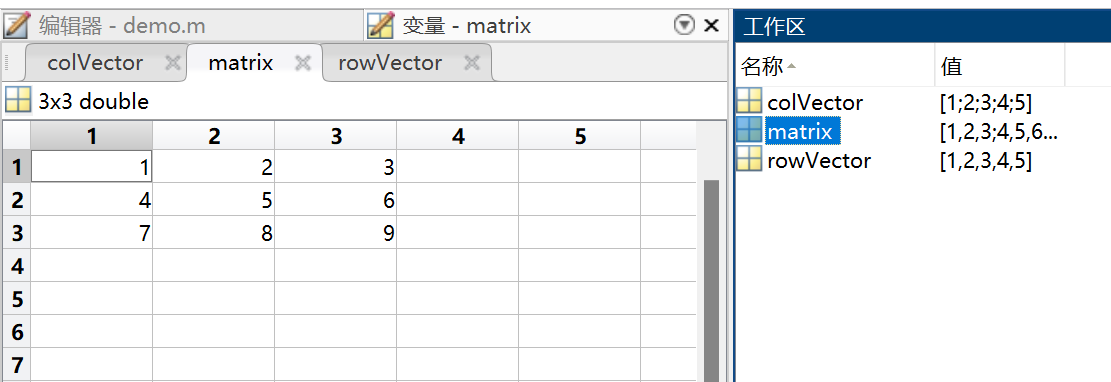
% 创建行向量
rowVector = [1, 2, 3, 4, 5];

% 创建列向量
colVector = [1; 2; 3; 4; 5];

% 创建矩阵
matrix = [1 2 3; 4 5 6; 7 8 9];

5.2 数组和矩阵的运算

MATLAB支持多种数组和矩阵运算，包括但不限于：

元素级运算：对数组或矩阵中的每个元素单独进行运算。使用.（点）操作符来指明元素级运算。

% 元素级乘法
result = [1, 2, 3] .* [4, 5, 6];

% 元素级幂运算
result = [1, 2, 3] .^ 2;

矩阵运算：进行传统的矩阵乘法、转置等运算。

% 矩阵乘法
A = [1 2; 3 4];
B = [5 6; 7 8];
result = A * B;

% 矩阵转置
result = A';

特殊矩阵运算：计算逆矩阵、行列式、特征值等。

% 矩阵逆
invA = inv(A);

% 矩阵行列式
detA = det(A);

% 矩阵特征值和特征向量
[V, D] = eig(A);

5.3 数组和矩阵的索引

MATLAB中的索引从1开始，可以用来访问数组或矩阵的特定元素、行、列或子矩阵。

% 访问矩阵的第二行第一列元素
element = matrix(2, 1);

% 获取矩阵的第一行
firstRow = matrix(1, :);

% 获取矩阵的一个子矩阵（前两行，前两列）
subMatrix = matrix(1:2, 1:2);

5.4 多维数组

MATLAB也支持多维数组，这在处理图像、时间序列数据或其他类型的多维数据时非常有用。

% 创建一个3x3x2的三维数组
threeDArray = cat(3, [1 2 3; 4 5 6; 7 8 9], [10 11 12; 13 14 15; 16 17 18]);

解决疑问：

张量是一个数学概念，广泛用于物理学和工程学，特别是在描述多维空间中的线性关系时。张量可以视为更高维度的数组，是向量和矩阵的推广。
在编程和机器学习领域，张量通常指的是一个可以有任意数量维度的多维数组。例如，在TensorFlow或PyTorch这样的深度学习框架中，张量是核心的数据结构，用于存储和操作多维数据集。

简而言之，可以认为向量是一维张量，矩阵是二维张量，而更高维度的数组（三维及以上）也可以称为张量。在MATLAB中，虽然通常不经常用“张量”这个术语，但MATLAB支持多维数组的概念，在很多方面与张量相似。

关于复杂网络建模，我前面写了很多，大家可以学习参考。

【复杂网络建模】——常用绘图软件和库_图论画图软件

【复杂网络建模】——Pytmnet进行多层网络分析与可视化

【复杂网络建模】——Python通过平均度和随机概率构建ER网络

【复杂网络建模】——通过图神经网络来建模分析复杂网络

【复杂网络建模】——Python可视化重要节点识别(PageRank算法)

【复杂网络建模】——基于Pytorch构建图注意力网络模型

【复杂网络建模】——Hypergraphx: 用于高阶网络分析的库

【复杂网络建模】——基于节点相似性的社团划分算法

【复杂网络建模】——链路预测算法及其应用

【复杂网络建模】——ER网络度分布、无标度网络度分布