今天是三道困难题，一刷可以先跳过。

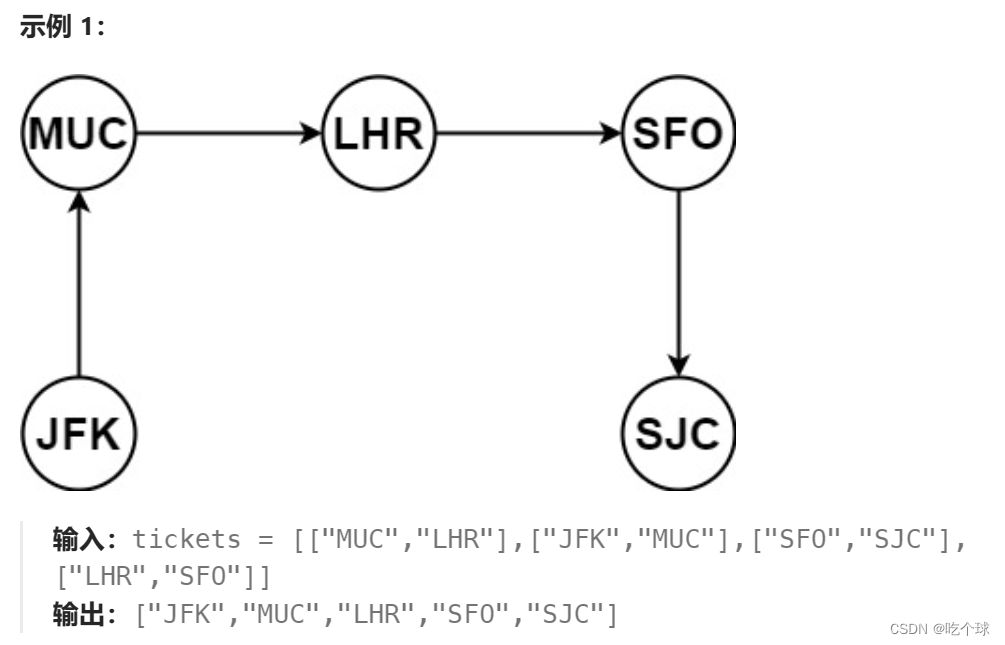
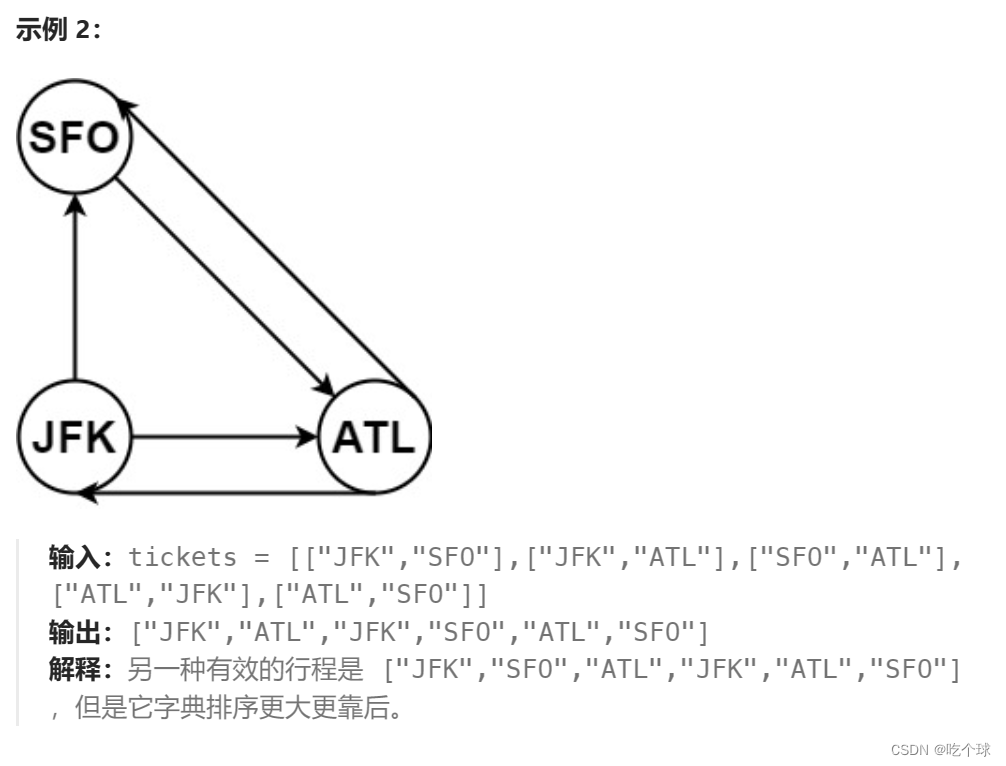
332.重新安排行程

本题的重点是使用Map<String,Map<String,Integer>>存储路径以便递归中根据上一个地点检索接下来的选择。注意，因为要求按字母顺序排列优先级，所以内层的Map要用TreeMap<String,Integer>。并且回溯的递归函数要有返回值（因为最终只需要获取一个路径）。

class Solution {
    private Deque<String> res;
    private Map<String, Map<String, Integer>> map;

    private boolean backTracking(int ticketNum){
        if(res.size() == ticketNum + 1){
            return true;
        }
        String last = res.getLast();
        if(map.containsKey(last)){//防止出现null
            for(Map.Entry<String, Integer> target : map.get(last).entrySet()){
                int count = target.getValue();
                if(count > 0){
                    res.add(target.getKey());
                    target.setValue(count - 1);
                    if(backTracking(ticketNum)) return true;
                    res.removeLast();
                    target.setValue(count);
                }
            }
        }
        return false;
    }

    public List<String> findItinerary(List<List<String>> tickets) {
        map = new HashMap<String, Map<String, Integer>>();
        res = new LinkedList<>();
        for(List<String> t : tickets){
            Map<String, Integer> temp;
            if(map.containsKey(t.get(0))){
                temp = map.get(t.get(0));
                temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
            }else{
                temp = new TreeMap<>();//升序Map
                temp.put(t.get(1), 1);
            }
            map.put(t.get(0), temp);

        }
        res.add("JFK");
        backTracking(tickets.size());
        return new ArrayList<>(res);
    }
}

51. N皇后

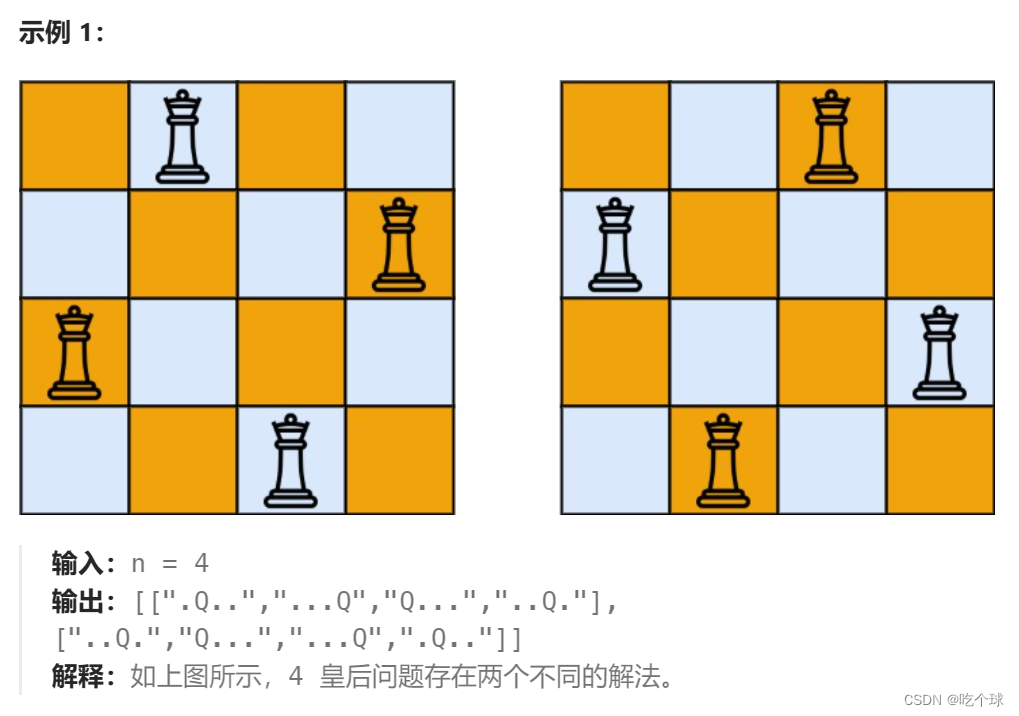
该题递归的深度是n，每一层递归是遍历当前行每个位置放皇后是否合法，树枝向下是行的增加，横向向右是列位置的遍历。
需要自定义一个判断当前位置是否合法的函数。

class Solution {
    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }


    public void backTrack(int n, int row, char[][] chessboard) {
        if (row == n) {
            res.add(Array2List(chessboard));
            return;
        }

        for (int col = 0;col < n; ++col) {
            if (isValid (row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backTrack(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }

    }


    public List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();

        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }


    public boolean isValid(int row, int col, int n, char[][] chessboard) {
        // 检查列
        for (int i=0; i<row; ++i) { // 相当于剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }

        // 检查45度对角线
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // 检查135度对角线
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
}

37. 解数独

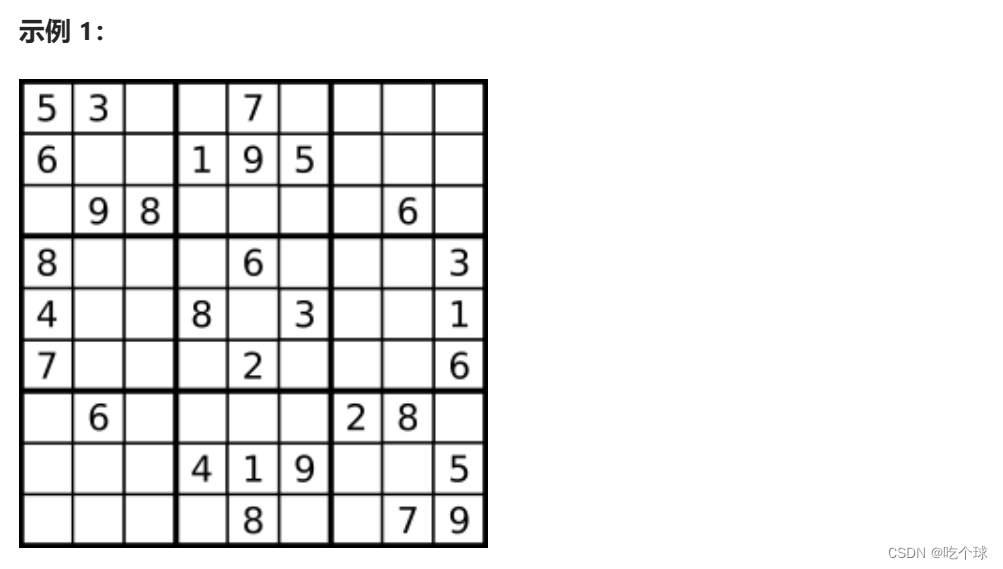
这道题需要再递归函数里进行两次for循环，第一层遍历行，第二层遍历列。
因为只需要找到一条符合条件的结果，因此只要找到了就返回true，因此返回值是boolean类型。

class Solution {
    public void solveSudoku(char[][] board) {
        solveSudokuHelper(board);
    }

    private boolean solveSudokuHelper(char[][] board){
        //「一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，
        // 一行一列确定下来之后，递归遍历这个位置放9个数字的可能性！」
        for (int i = 0; i < 9; i++){ // 遍历行
            for (int j = 0; j < 9; j++){ // 遍历列
                if (board[i][j] != '.'){ // 跳过原始数字
                    continue;
                }
                for (char k = '1'; k <= '9'; k++){ // (i, j) 这个位置放k是否合适
                    if (isValidSudoku(i, j, k, board)){
                        board[i][j] = k;
                        if (solveSudokuHelper(board)){ // 如果找到合适一组立刻返回
                            return true;
                        }
                        board[i][j] = '.';
                    }
                }
                // 9个数都试完了，都不行，那么就返回false
                return false;
                // 因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！
                // 那么会直接返回， 「这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！」
            }
        }
        // 遍历完没有返回false，说明找到了合适棋盘位置了
        return true;
    }

    /**
     * 判断棋盘是否合法有如下三个维度:
     *     同行是否重复
     *     同列是否重复
     *     9宫格里是否重复
     */
    private boolean isValidSudoku(int row, int col, char val, char[][] board){
        // 同行是否重复
        for (int i = 0; i < 9; i++){
            if (board[row][i] == val){
                return false;
            }
        }
        // 同列是否重复
        for (int j = 0; j < 9; j++){
            if (board[j][col] == val){
                return false;
            }
        }
        // 9宫格里是否重复
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++){
            for (int j = startCol; j < startCol + 3; j++){
                if (board[i][j] == val){
                    return false;
                }
            }
        }
        return true;
    }
}