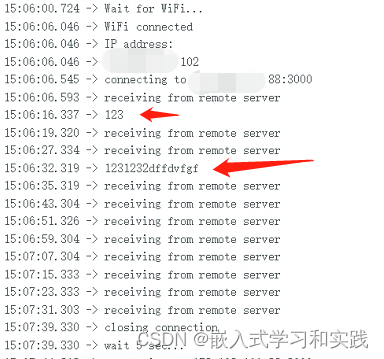
目录
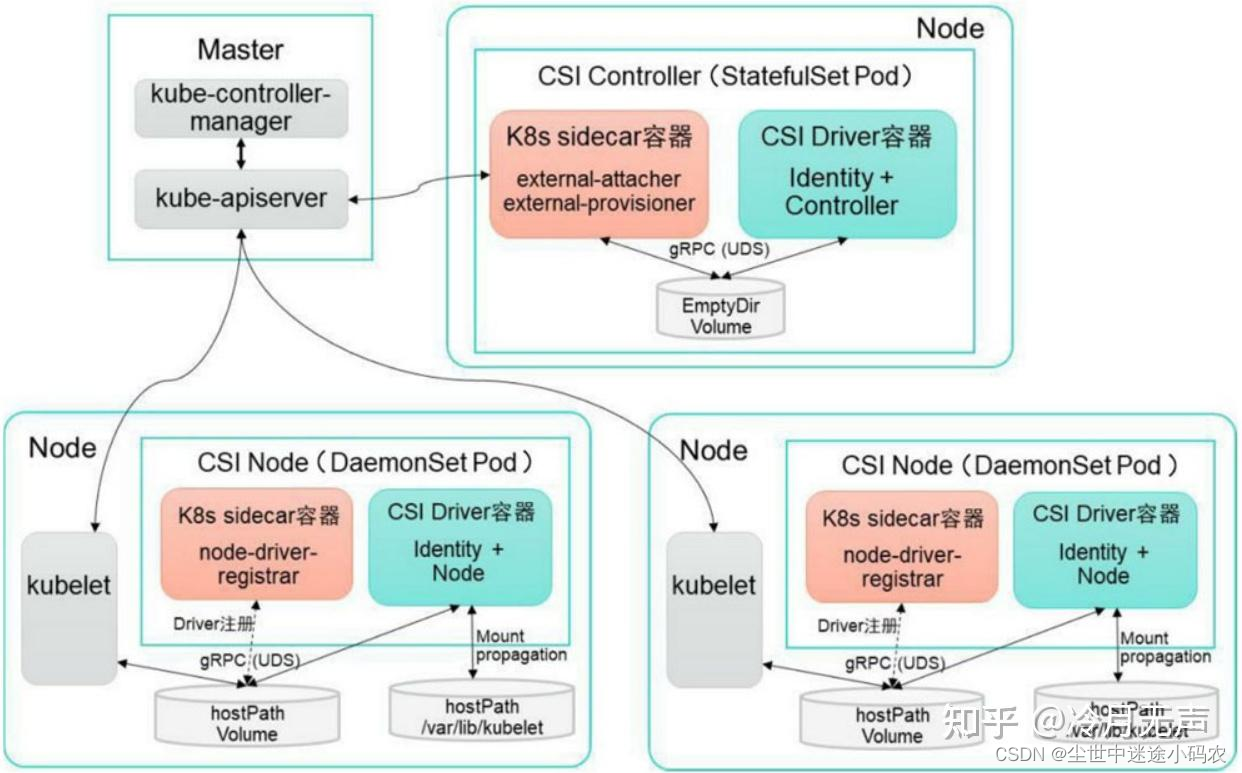
无向图
有向图
邻接矩阵
邻接表
图的bfs,dfs
二部图(二分图)
有向无环图(DAG)
拓扑排序(Topological Sort)
AOV网
迪杰斯特拉Dijkstra
最小生成树
克鲁斯卡尔:Kruskal
普里姆:prim
图是多对多关系,是顶点和边的二元组和。
无向图
1.依附关系:边(v1,v2)依附于顶点v1,v2。
2.完全图:所有可能的边都存在。
3.路径:一个点到另一个点的边。
4.简单路径:除起点终点可能相同外,其他点不允许重复出现。
5.连通:有路径可通。(有n个点,可能联通需要n-1条边,一定能联通,拿掉一个点完全联通图+1)
6.连通图:图中所有点之间均有路径可通。
7.子图:子图顶点集合原顶点集合,边集合
边集合。
8.极大连通子图(连通分量):画圈的就是。

有向图
1.连通图:相异成对顶点间路径可通。
2.极大连通子图(强连通分量):成对顶点间均有路径可通。
3.用<v1,v2>。
邻接矩阵
边多适用,唯一。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 1 | 1 |
| 4 | 1 | 0 | 1 | 0 | 1 |
| 5 | 0 | 1 | 1 | 1 | 0 |
邻接表
边少适用,不唯一。


图的bfs,dfs
图的创建:(1)顶点个数(2)申请并初始化(3)放边
DFS:(1)标记数组(2)遍历:1.打印顶点2.标记(3)标记邻接点,找邻接的未处理过的同(2)
BFS:(1)Queue(2)标记初始化(3)起始顶点入队标记(4)处理:弹出,打印,遍历邻接点,未处理邻接点入队,标记,等待处理重复(4)
#include<iostream>
#include<string.h>
#include<queue>
using namespace std;
typedef struct node
{
int nedge;
int nV;
int* pjuzhen;
}Graph;
Graph* Create()
{
Graph* pGraph = (Graph*)malloc(sizeof(Graph));
//顶点个数,边的条数
int nv, ne;
cin >> nv >> ne;
pGraph->nedge = ne;
pGraph->nV = nv;
pGraph->pjuzhen = (int*)malloc(sizeof(Graph) * nv * nv);
memset(pGraph->pjuzhen, 0, sizeof(Graph) * nv * nv);
for (int i = 0; i < ne; i++)
{
int v1, v2;
cin >> v1 >> v2;
if (v1>=1&& v1<=nv&&v2>=1&&v2<=nv&&v1!=v2&&pGraph->pjuzhen[(v1 - 1) * nv + v2 - 1] == 0)
{
pGraph->pjuzhen[(v1 - 1) * nv + v2 - 1] = 1;
pGraph->pjuzhen[(v2 - 1) * nv + v1 - 1] = 1;
}
else i--;
}
return pGraph;
}
void DFSGraph(Graph* pGraph, int fir, int* pMark)
{
cout << fir << " ";
pMark[fir - 1] = 1;
for (int i = 0; i < pGraph->nV; i++)
{
if (pGraph->pjuzhen[(fir - 1) * pGraph->nV + i] == 1 && pMark[i] == 0)
{
DFSGraph(pGraph, i + 1, pMark);
}
}
}
void BFS(Graph* pGraph, int fir)
{
if (pGraph == NULL || fir<1 || fir>pGraph->nV)return;
int* pMark = NULL;
pMark = (int*)malloc(sizeof(int) * pGraph->nV);
memset(pMark, 0, sizeof(int) * pGraph->nV);
queue<int>q;
q.push(fir);
pMark[fir - 1] = 1;
while (!q.empty())
{
fir = q.front();
q.pop();
cout << fir << " ";
for (int i = 0; i < pGraph->nV; i++)
{
if (pGraph->pjuzhen[(fir - 1) * pGraph->nV + i] == 1 && pMark[i] == 0)
{
q.push(i + 1);
pMark[i] = 1;
}
}
}free(pMark);
pMark = NULL;
}
void DFS(Graph* pGraph,int fir)
{
if (pGraph == NULL || fir < 1 || fir>pGraph->nV)return;
int* pMark=NULL;
pMark = (int*)malloc(sizeof(int)*pGraph->nV);
memset(pMark, 0, sizeof(int) * pGraph->nV);
DFSGraph(pGraph, fir, pMark);
free(pMark);
pMark = NULL;
}
int main()
{
Graph* p = Create();
for (int i = 0; i < p->nV * p->nV; i++)
{
if (i % p->nV == 0)cout << endl;
cout << p->pjuzhen[i] << " ";
}
cout << endl;
DFS(p, 2);
cout << endl;
BFS(p, 4);
cout << endl;
return 0;
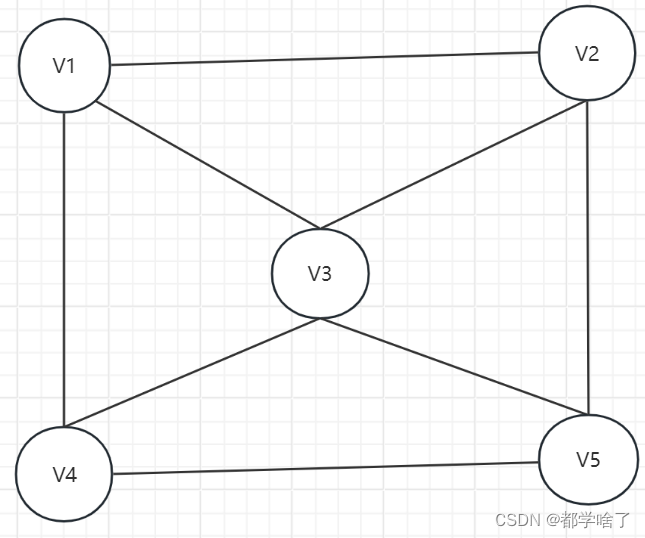
}二部图(二分图)
G=(u,v,e),u,v都是顶点集合,边是发生在集合之间的,但是集合内部没边关系。
例如:这个就不是,因为v2和v4是一个集合的它们相连了。
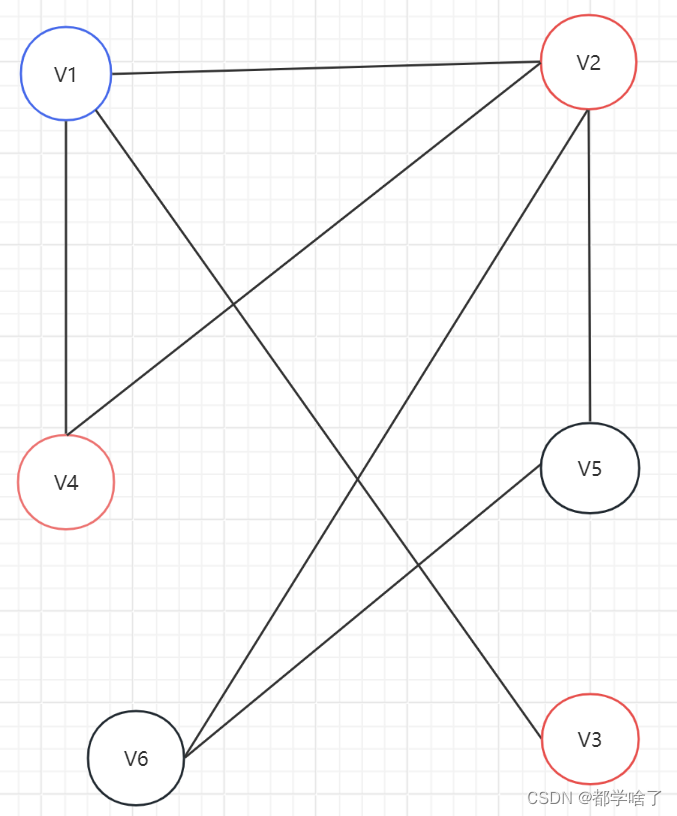
例如:这个就是。

有向无环图(DAG)
例:
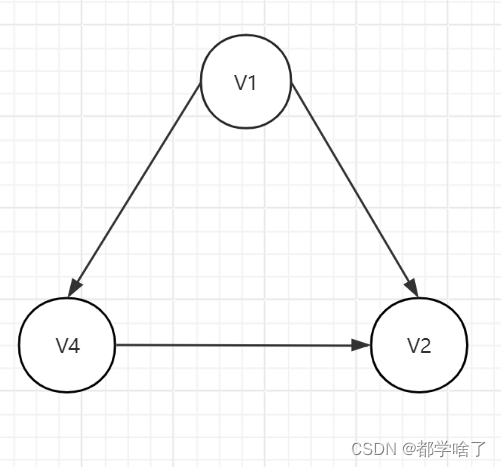
有向无环图一定有拓扑排序。
拓扑排序(Topological Sort)
为一个项目内具各依赖关系的活动求得可执行的线性顺序。这个线性顺序叫拓扑序列。
拓扑序列:若从顶点vi到vj有一条路径,则在顶点的拓扑序列中顶点vi必在顶点vj之前。
有拓扑排序的一定是DAG。
AOV网
AOV没有回路的前提下,可以将全部活动排序列成拓扑序列。

步骤:
(1)统计所有顶点入度。
(2)创建队列。
(3)入度为0的节点入队。
(4)处理 :出队,所有邻接点的入度更新,新的入度为0的节点入队。
迪杰斯特拉Dijkstra
点到点的最短路径:
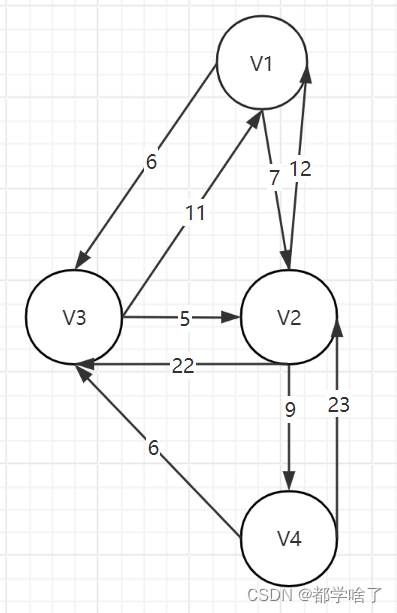
| v1 | v2 | v3 | v4 | |
| v1 | 0 | 7 | 6 | 0 |
| v2 | 12 | 0 | 22 | 9 |
| v3 | 11 | 5 | 0 | 0 |
| v4 | 0 | 23 | 6 | 0 |
这里写一下v1到各个点的最短距离。
v1{0,7,6,0} (找数最小不为0的点)
v1,v3{0,7,6,0} (v3->v2为5,5+6<7,所以为7,v3到不了v4还是为0)
v1,v3,v2{0,7,6,16} (v2->v4为9,9+7=16)
最小生成树
克鲁斯卡尔:Kruskal
按路径长度从小到大排序,如果两点已经连通就跳过。
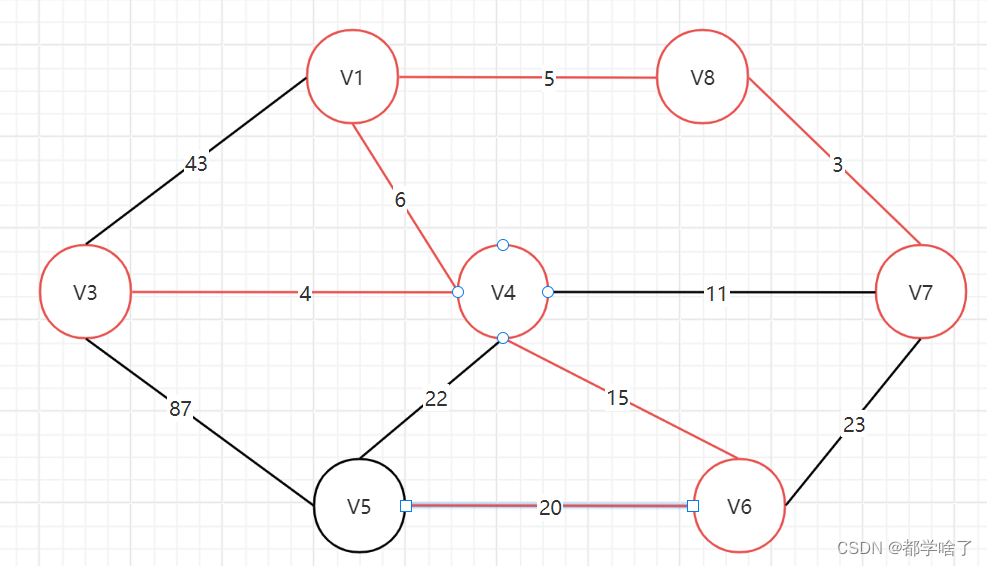
例:

先是3,4,5,6路径连上。
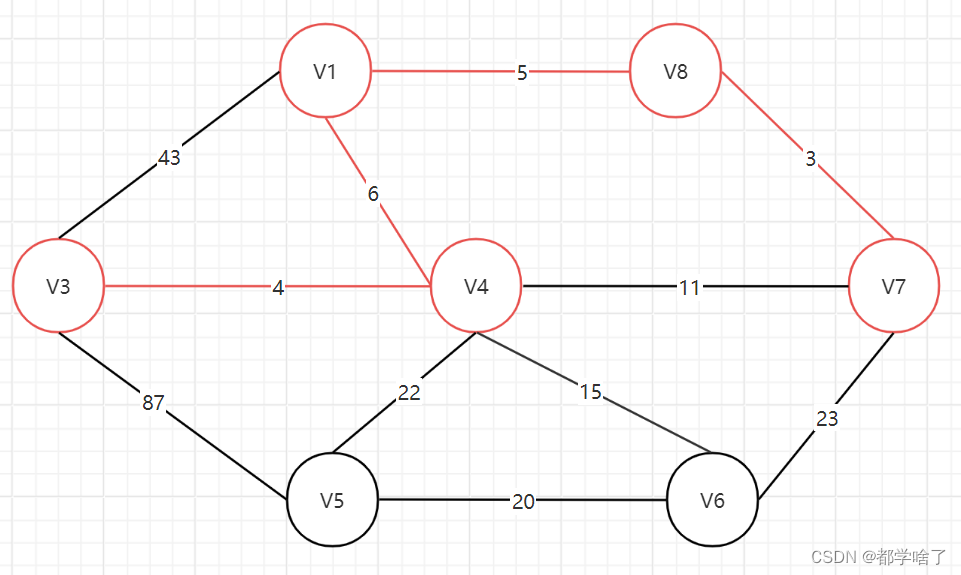
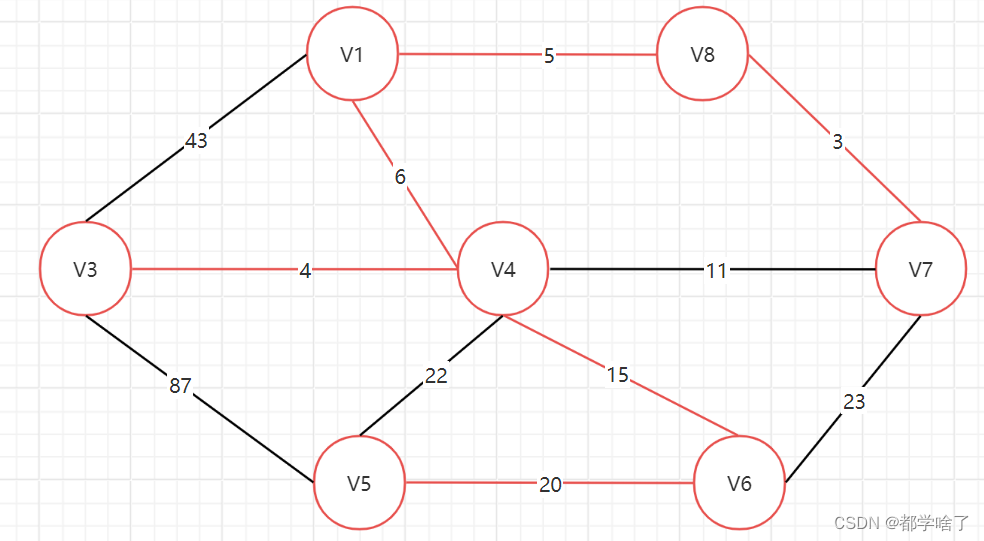
由于v4,v7已经联通所以跳过11。
连上15,20,结束。
普里姆:prim
假设从v1节点寻找。
v1->v3,v1->v4,v1->v8中v1->v8最小。
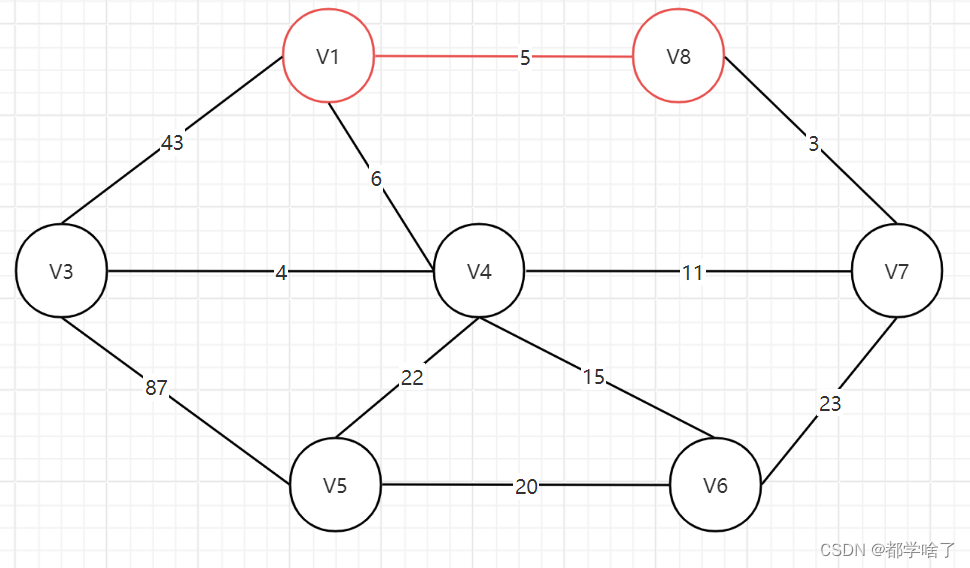
v1->v3,v1->v4,v8->v7中v8->v7最小,所以选v8->v7。

v1->v3,v1->v4,v7->v4,v7->v6中,v1->v4最小,选v1->v4。
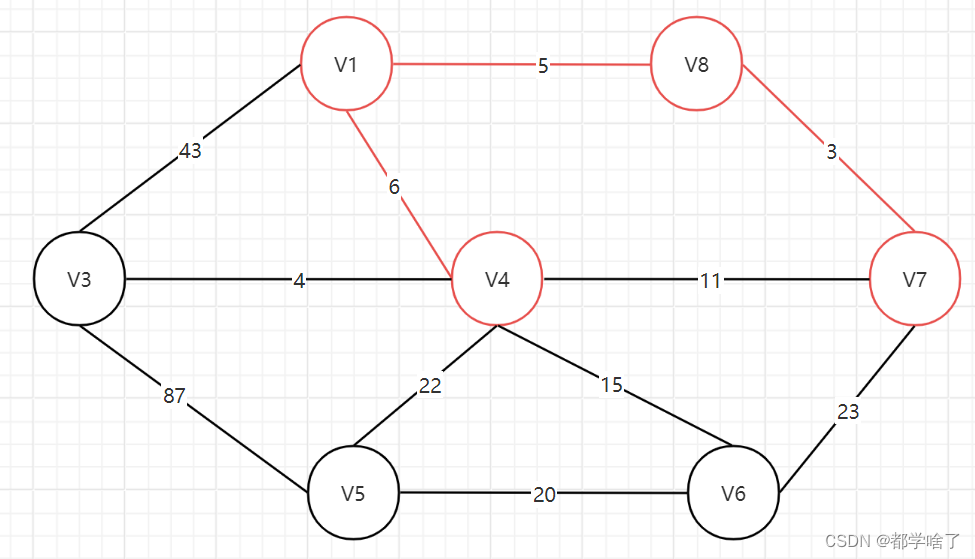
v1->v3,v4->v3,v4->v5,v4->v6,v7->v6中,v4->v3最小,选v4->v3。

后续同理(由于v4,v7已经连通所以看下一个15)。
结果: