目录
介绍:
模板:
案例:
极小型指标转化为极大型(正向化):
中间型指标转为极大型(正向化):
区间型指标转为极大型(正向化):
标准化处理:
公式:
Topsis(优劣解距离法):
公式:
完整代码:
结果:
介绍:
在数学建模中,Topsis方法是一种多准则决策分析方法,用于评估和排序备选方案。它代表了“最佳方案相似性排序技术”。
在Topsis方法中,每个备选方案根据一组准则进行评估,并分配权重,以反映它们的相对重要性。然后,该方法根据每个备选方案与理想解和负理想解之间的差异计算两个度量值:到理想解的距离和到负理想解的距离。
理想解代表了每个准则的最佳可能值,而负理想解则代表了最差可能值。这些距离度量值使用一个公式计算,考虑了备选方案与这两个参考点之间差异的加权总和。
一旦计算出距离,Topsis根据备选方案与理想解的接近度对其进行排序。与理想解最接近且与负理想解最远的备选方案被视为最佳选择。
Topsis方法常用于需要考虑多个准则的决策情景中,例如选择供应商、评估项目或选择最佳行动方案。它帮助决策者客观地评估和比较备选方案,同时考虑到每个选项的正面和负面因素。
模板:
import numpy as np
def topsis(data, weights, impacts):
# 数据归一化
normalized_data = data / np.sqrt(np.sum(data**2, axis=0))
# 加权归一化数据
weighted_normalized_data = normalized_data * weights
# 理想解和负理想解
ideal_solution = np.max(weighted_normalized_data, axis=0)
negative_ideal_solution = np.min(weighted_normalized_data, axis=0)
# 计算备选方案与理想解和负理想解的距离
distances = np.sqrt(np.sum((weighted_normalized_data - ideal_solution)**2, axis=1)) / \
np.sqrt(np.sum((weighted_normalized_data - negative_ideal_solution)**2, axis=1))
# 考虑权重和影响的得分
scores = np.sum(weights * impacts * normalized_data, axis=1)
# 综合得分
comprehensive_scores = scores / (scores + distances)
# 排序并返回结果
rankings = np.argsort(comprehensive_scores)[::-1] + 1
return rankings
# 例子
data = np.array([[3, 2, 5, 4],
[4, 1, 2, 8],
[1, 3, 4, 6],
[2, 4, 3, 5]])
weights = np.array([0.25, 0.25, 0.25, 0.25])
impacts = np.array([1, 1, -1, 1])
rankings = topsis(data, weights, impacts)
print(rankings)
案例:


极小型指标转化为极大型(正向化):
# 公式:max-x
if ('Negative' in name) == True:
max0 = data_nor[columns_name[i + 1]].max()#取最大值
data_nor[columns_name[i + 1]] = (max0 - data_nor[columns_name[i + 1]]) # 正向化
# print(data_nor[columns_name[i+1]])中间型指标转为极大型(正向化):
# 中间型指标正向化 公式:M=max{|xi-best|} xi=1-|xi-best|/M
if ('Moderate' in name) == True:
print("输入最佳值:")
max = data_nor[columns_name[i + 1]].max()
min = data_nor[columns_name[i + 1]].min()
best=input()
M=0
for j in data_nor[columns_name[i + 1]]:
if(M<abs(j-int(best))):
M=(abs(j-int(best)))
data_nor[columns_name[i + 1]]=1-(abs(data_nor[columns_name[i + 1]]-int(best))/M)
#print(data_nor[columns_name[i + 1]])
区间型指标转为极大型(正向化):
# 区间型指标正向化
if('Section' in name)==True:
print()
print("输入区间:")
a=input()
b=input()
a=int(a)
b=int(b)
max = data_nor[columns_name[i + 1]].max()
min= data_nor[columns_name[i + 1]].min()
if(a-min>max-b):
M=a-min
else:
M=max-b
#print(data_nor[columns_name[i + 1]][0])
cnt=0
for j in data_nor[columns_name[i + 1]]:
if(j<int(a)):
data_nor[columns_name[i + 1]][cnt]=1-(a-j)/M
elif (int(a)<= j <=int(b)):
data_nor[columns_name[i + 1]][cnt]=1
elif (j>b):
data_nor[columns_name[i + 1]][cnt]=1-(j-b)/M
#print(data_nor[columns_name[i + 1]][cnt])
cnt+=1
#print(data_nor[columns_name[i + 1]])
'''公式:
M = max{a-min{xi},max{xi}-b} xi<a,则xi=1-(a-xi)/M; a<=xi<=b,则xi=1; xi>b,则1-(xi-b)/M
'''标准化处理:
公式:

def normalization(data_nor):
data_nors = data_nor.values
data_nors = np.delete(data_nors, 0, axis=1)#去掉第一行
squere_A = data_nors * data_nors#矩阵相乘
# print(squere_A)
sum_A = np.sum(squere_A, axis=0)#按列求和
sum_A = sum_A.astype(float)
stand_A = np.sqrt(sum_A)#平方根
columns_name = data_nor.columns.values
cnt=0
for i in columns_name[1:]:
#print(data_nor[i])
data_nor[i]=data_nor[i]/stand_A[cnt]
cnt+=1
#print(data_nor)
return data_nor
Topsis(优劣解距离法):
公式:

def topsis(data):
data_nor=data.copy()
data_nor=data_nor.values
data_nor = np.delete(data_nor, 0, axis=1)
z_max=np.amax(data_nor,axis=0)#每个特征里面挑最大值
z_min=np.amin(data_nor,axis=0)#每个特征里面挑最小值
#print(z_min)
#print(z_max)
tmpmaxdist=np.power(np.sum(np.power((z_max-data_nor),2),axis=1),0.5)#最大距离
tmpmindist=np.power(np.sum(np.power((z_min-data_nor),2),axis=1),0.5)#最小距离
score=tmpmindist/(tmpmindist+tmpmaxdist)#定义得分
score = score/np.sum(score)#归一化
return score完整代码:
#coding=gbk
import pandas as pd
import numpy as np
import re
import warnings
# 定义文件读取方法
def read_data(file):
file_path = file
raw_data = pd.read_excel(file_path, header=0)
# print(raw_data)
return raw_data
# 定义数据正向化
def data_normalization(data):
data_nor = data.copy()
columns_name = data_nor.columns.values
#print(columns_name)
for i in range((len(columns_name) - 1)):
name = columns_name[i + 1]
print("输入这一类数据类型(Positive、Negative、Moderate、Section:)")
name=input()
# 极小型指标正向化
if ('Negative' in name) == True:
max0 = data_nor[columns_name[i + 1]].max()#取最大值
data_nor[columns_name[i + 1]] = (max0 - data_nor[columns_name[i + 1]]) # 正向化
# print(data_nor[columns_name[i+1]])
# 中间型指标正向化
if ('Moderate' in name) == True:
print("输入最佳值:")
max = data_nor[columns_name[i + 1]].max()#取最大值
min = data_nor[columns_name[i + 1]].min()#取最小值
best=input()
best=int(float(best))
M=0
for j in data_nor[columns_name[i + 1]]:
if(M<abs(j-int(best))):
M=(abs(j-int(best)))
data_nor[columns_name[i + 1]]=1-(abs(data_nor[columns_name[i + 1]]-int(best))/M)
#print(data_nor[columns_name[i + 1]])
# 区间型指标正向化
if('Section' in name)==True:
print("输入区间:")
a=input()
b=input()
a=int(a)
b=int(b)
max = data_nor[columns_name[i + 1]].max()
min= data_nor[columns_name[i + 1]].min()
if(a-min>max-b):
M=a-min
else:
M=max-b
#print(data_nor[columns_name[i + 1]][0])
cnt=0
for j in data_nor[columns_name[i + 1]]:
if(j<int(a)):
data_nor[columns_name[i + 1]][cnt]=1-(a-j)/M
elif (int(a)<= j <=int(b)):
data_nor[columns_name[i + 1]][cnt]=1
elif (j>b):
data_nor[columns_name[i + 1]][cnt]=1-(j-b)/M
cnt+=1
#print(data_nor[columns_name[i + 1]])
# print(data_nor)
return data_nor
def normalization(data_nor):
data_nors = data_nor.values
data_nors = np.delete(data_nors, 0, axis=1)
squere_A = data_nors * data_nors#矩阵相乘
# print(squere_A)
sum_A = np.sum(squere_A, axis=0)#按列求和
sum_A = sum_A.astype(float)
stand_A = np.sqrt(sum_A)#开平方
columns_name = data_nor.columns.values
cnt=0
for i in columns_name[1:]:
data_nor[i]=data_nor[i]/stand_A[cnt]#每个元素除以相对应的平方根
cnt+=1
#print(data_nor)
return data_nor
# 定义计算熵权方法
def entropy_weight(data_nor):
columns_name = data_nor.columns.values
n = data_nor.shape[0]
E = []
for i in columns_name[1:]:
# 计算信息熵
# print(i)
data_nor[i] = data_nor[i] / sum(data_nor[i])
data_nor[i] = data_nor[i] * np.log(data_nor[i])
data_nor[i] = data_nor[i].where(data_nor[i].notnull(), 0)
# print(data_nor[i])
Ei = (-1) / (np.log(n)) * sum(data_nor[i])
E.append(Ei)
# print(E)
# 计算权重
W = []
for i in E:
wi = (1 - i) / ((len(columns_name) - 1) - sum(E))
W.append(wi)
# print(W)
return W
# 计算得分
def entropy_score(data, w):
data_s = data.copy()
columns_name = data_s.columns.values
for i in range((len(columns_name) - 1)):
name = columns_name[i + 1]
data_s[name] = data_s[name] * w[i]
return data_s
def topsis(data):
data_nor=data.copy()
data_nor=data_nor.values
data_nor = np.delete(data_nor, 0, axis=1)
z_max=np.amax(data_nor,axis=0)#每个特征里面挑最大值
z_min=np.amin(data_nor,axis=0)#每个特征里面挑最小值
#print(z_min)
#print(z_max)
tmpmaxdist=np.power(np.sum(np.power((z_max-data_nor),2),axis=1),0.5)#最大距离
tmpmindist=np.power(np.sum(np.power((z_min-data_nor),2),axis=1),0.5)#最小距离
score=tmpmindist/(tmpmindist+tmpmaxdist)#定义得分
score = score/np.sum(score)#归一化
return score
if __name__ == "__main__":
file = 'filepath' # 声明数据文件地址
data = read_data(file) # 读取数据文件
data_nor = data_normalization(data) # 数据正向化,生成后的数据data_nor
print("\n正向化后的数据:")
print(data_nor)
data_nor=normalization(data_nor)
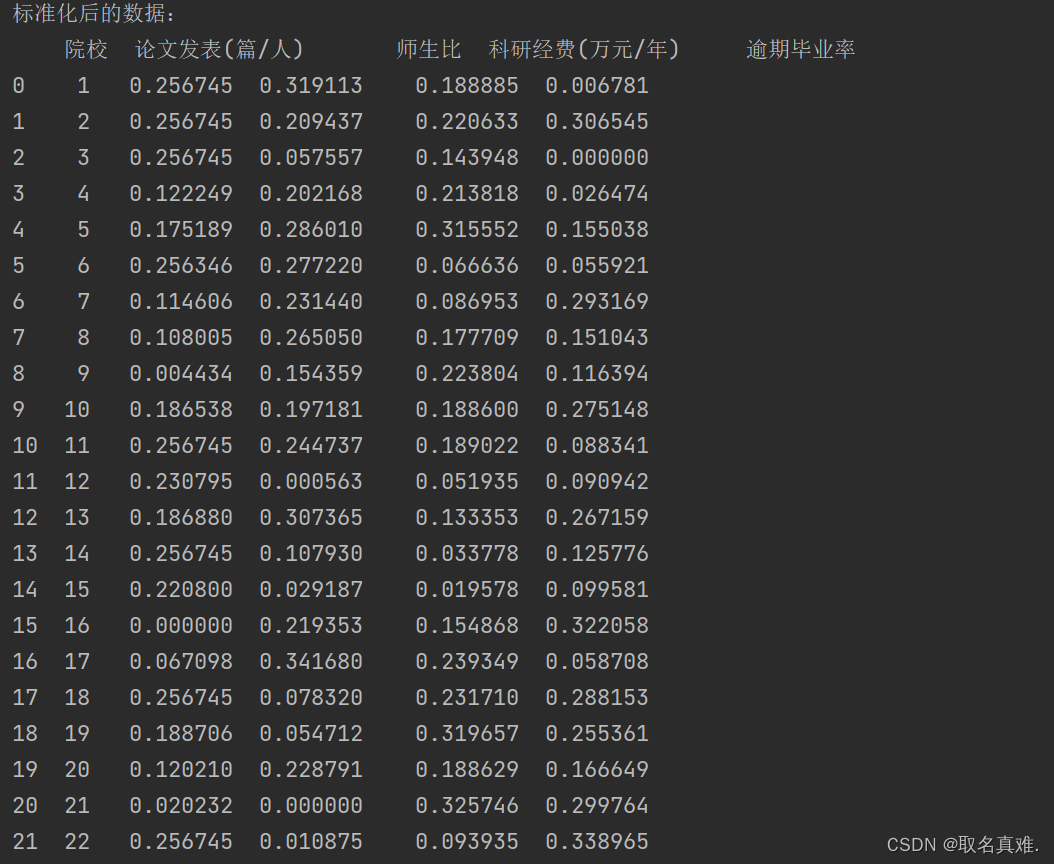
print("\n标准化后的数据:")
print(data_nor)
score=topsis(data_nor)
print("\n得分:")
print(score)
score=pd.DataFrame(score)
score.columns=["得分"]
data=pd.DataFrame(data)
data=pd.concat([data,score],axis=1)
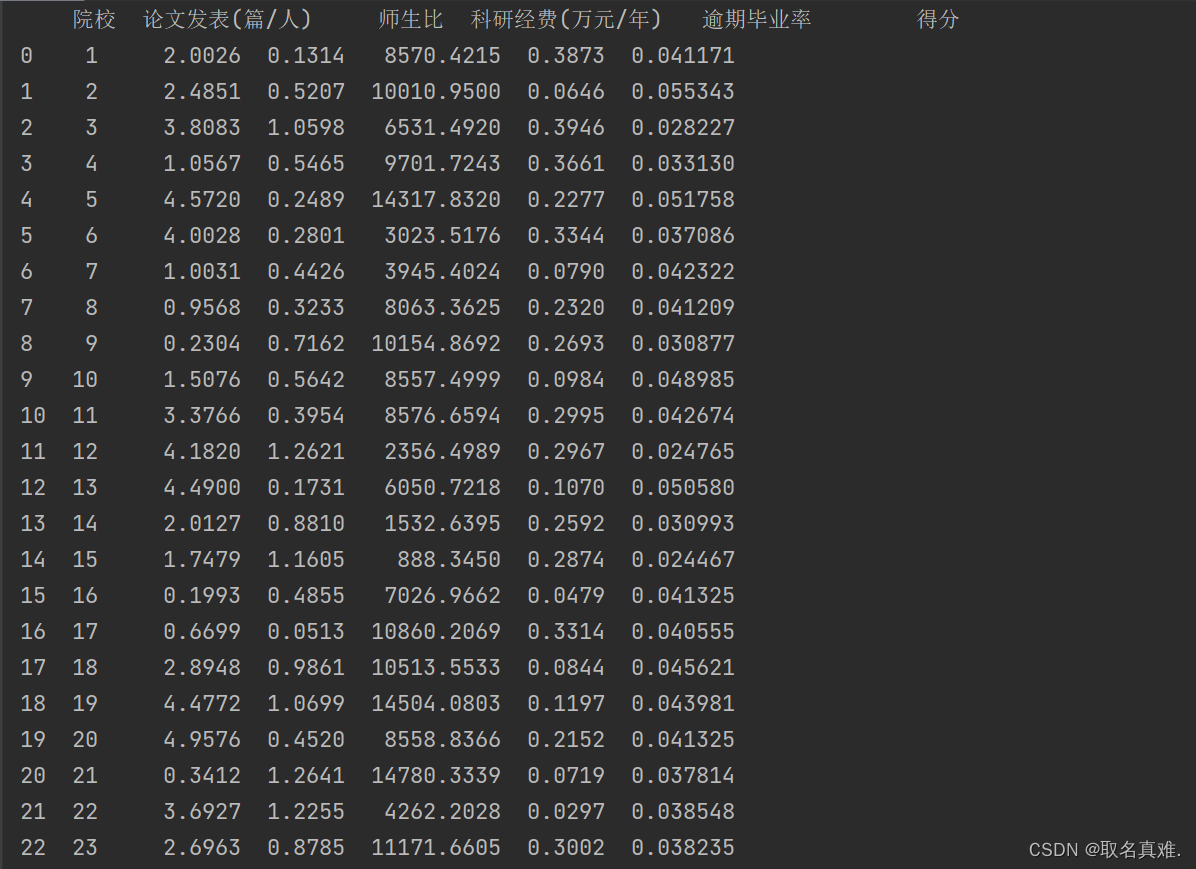
print(data)
结果: