目录
- 矩阵
- 矩阵置零
- 螺旋矩阵
- 旋转图像
- 搜索二维矩阵 II
LeetCode 73. 矩阵置零
LeetCode 54. 螺旋矩阵
LeetCode 48. 旋转图像
LeetCode 240. 搜索二维矩阵 II
矩阵
矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
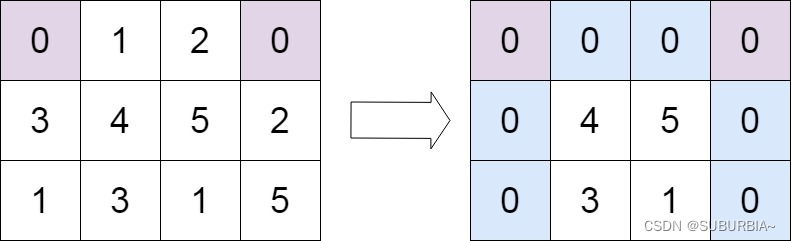
- 用 O ( m + n ) O(m + n) O(m+n) 额外空间
- 两遍扫 matrix, 第一遍用集合记录哪些行,哪些列有0 , 第二遍置 0
class Solution {
public void setZeroes(int[][] matrix) {
Set<Integer> row_zero = new HashSet<>();
Set<Integer> col_zero = new HashSet<>();
int row = matrix.length;
int col = matrix[0].length;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (matrix[i][j] == 0) {
row_zero.add(i);
col_zero.add(j);
}
}
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (row_zero.contains(i) || col_zero.contains(j)) {
matrix[i][j] = 0;
}
}
}
}
}
- 用 O ( 1 ) O(1) O(1) 空间
- 用 matrix 第一行和第一列记录该行该列是否有0,作为标志位
- 但是对于第一行,和第一列要设置一个标志位,为了防止自己这一行(一列)也有0的情况.
class Solution {
public void setZeroes(int[][] matrix) {
int row = matrix.length;
int col = matrix[0].length;
boolean row_flag = false;
boolean col_flag = false;
// 第一行有没有0
for (int j = 0; j < col; j++) {
if (matrix[0][j] == 0) {
row_flag = true;
break;
}
}
// 第一列有没有0
for (int i = 0; i < row; i++) {
if (matrix[i][0] == 0) {
col_flag = true;
break;
}
}
// 把第一行第一列作为标志位
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
// 置0
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
if (row_flag) {
for (int j = 0; j < col; j++) {
matrix[0][j] = 0;
}
}
if (col_flag) {
for (int i = 0; i < row; i++) {
matrix[i][0] = 0;
}
}
}
}
- 一个标记

class Solution {
public void setZeroes(int[][] matrix) {
boolean col_flag = false;
int row = matrix.length;
int col = matrix[0].length;
for (int i = 0; i < row; i++) {
if (matrix[i][0] == 0) col_flag = true;
for (int j = 1; j < col; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
for (int i = row - 1; i >= 0; i--) {
for (int j = col - 1; j >= 1; j--) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
if (col_flag) matrix[i][0] = 0;
}
}
}
螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
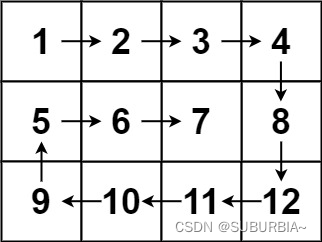
- 别怕设变量
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
if (matrix.length == 0) {
return new ArrayList<Integer>();
}
int l = 0, r = matrix[0].length - 1;
int t = 0, b = matrix.length - 1;
List<Integer> list = new ArrayList<>();
while (true) {
for (int i = l; i <= r; i++) {
list.add(matrix[t][i]); // left to right
}
if (++t > b) break;
for (int i = t; i <= b; i++) {
list.add(matrix[i][r]);
}
if (l > --r) break;
for (int i = r; i >= l; i--) {
list.add(matrix[b][i]);
}
if (t > --b) break;
for (int i = b; i >= t; i--) {
list.add(matrix[i][l]);
}
if (++l > r) break;
}
return list;
}
}
旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
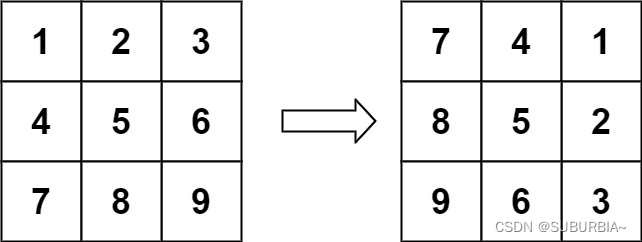

class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1)/ 2; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - 1- j][i];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
}
搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
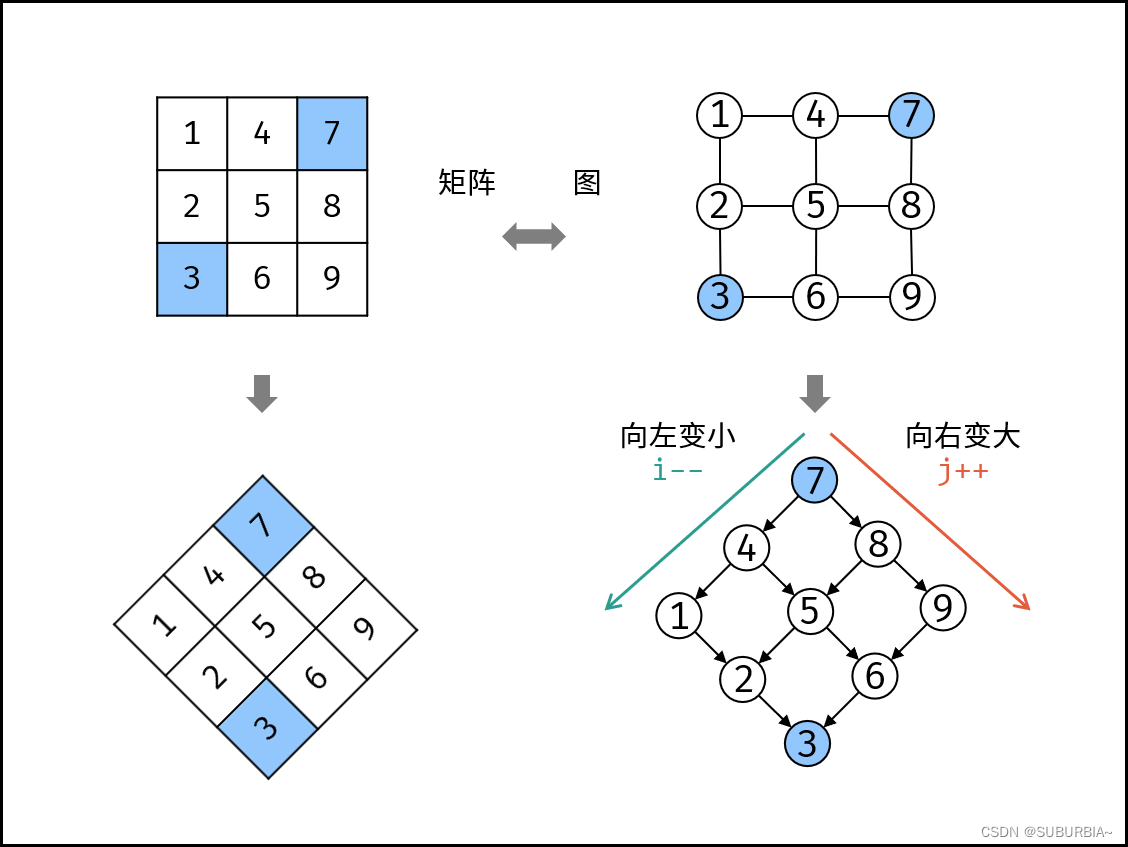
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int i = matrix.length - 1, j = 0;
while (i >= 0 && j < matrix[0].length) {
if (matrix[i][j] > target) {
i--;
} else if (matrix[i][j] < target) {
j++;
} else return true;
}
return false;
}
}