二叉搜索树（二叉排序树）（含力扣相关题及题解）

news2024/9/23 13:18:45

文章目录

  • 二叉搜索树（二叉排序树）
    • 1、二叉搜索树概念
    • 2、二叉搜索树的操作
      • 2.1、二叉搜索树的查找
      • 2.2、二叉搜索树的插入
      • 2.2、二叉树的删除
    • 3、二叉搜索树的实现（含递归版本）
    • 4、二叉搜索树的应用
      • 4.1、K模型
      • 4.2、KV模型
    • 5、二叉搜索树的性能分析
    • 6、二叉树进阶面试题

img

二叉搜索树（二叉排序树）

1、二叉搜索树概念

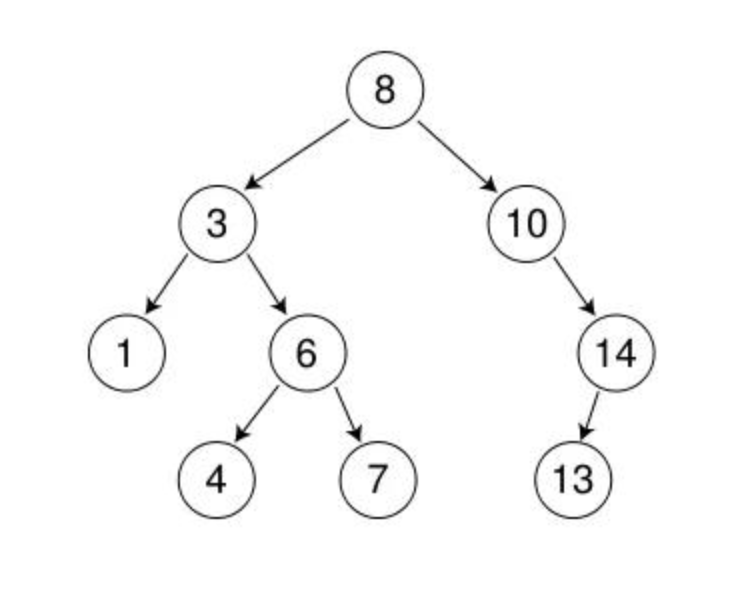
**二叉搜索树又叫二叉排序树和二叉查找树。**二叉搜索树可以为空。若当前二叉搜索树不为空，它有以下性质：

  1. 若左子树不为空，则根结点的的值大于左子树中所有结点的值

  2. 若右子树不为空，则根结点的的值小于左子树中所有结点的值

  3. 左右子树也有以上性质

2、二叉搜索树的操作

插入序列：

int arr[] = {8,3,1,10,6,4,7,14,13};

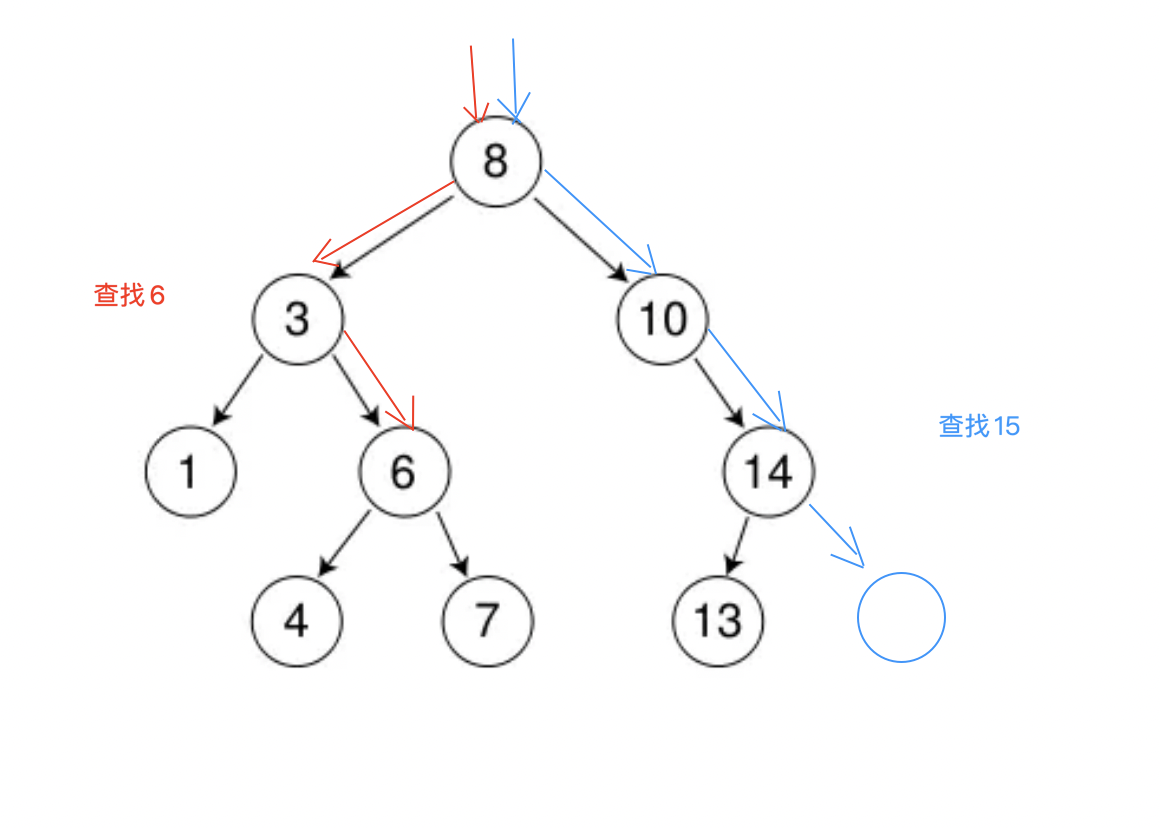
2.1、二叉搜索树的查找

  1. 从根开始比较，比根小的去根的左子树中查找，比根大的去根的右子树中查找
  2. 一直查找直到找到，没找到的话则走到了空。

template<class K>
struct BSTreeNode {
    //typedef BSTreeNode<K> Node;

    BSTreeNode<K> *_left;
    BSTreeNode<K> *_right;
    K _key;

    BSTreeNode(const K &key) : _left(nullptr), _right(nullptr), _key(key) {}

};


template<class K>
class BinarySearchTree {
public:
    typedef BSTreeNode<K> Node;
  
		bool Find(const K &key) {
        Node *cur = _root;
        if (cur == nullptr)
            return false;

        while (cur) {
            if (cur->_key < key) {
                cur = cur->_right;
            } else if (cur->_key > key) {
                cur = cur->_left;
            } else {
                return true;
            }
        }

        return false;
    }
private:
    Node *_root = nullptr;
};

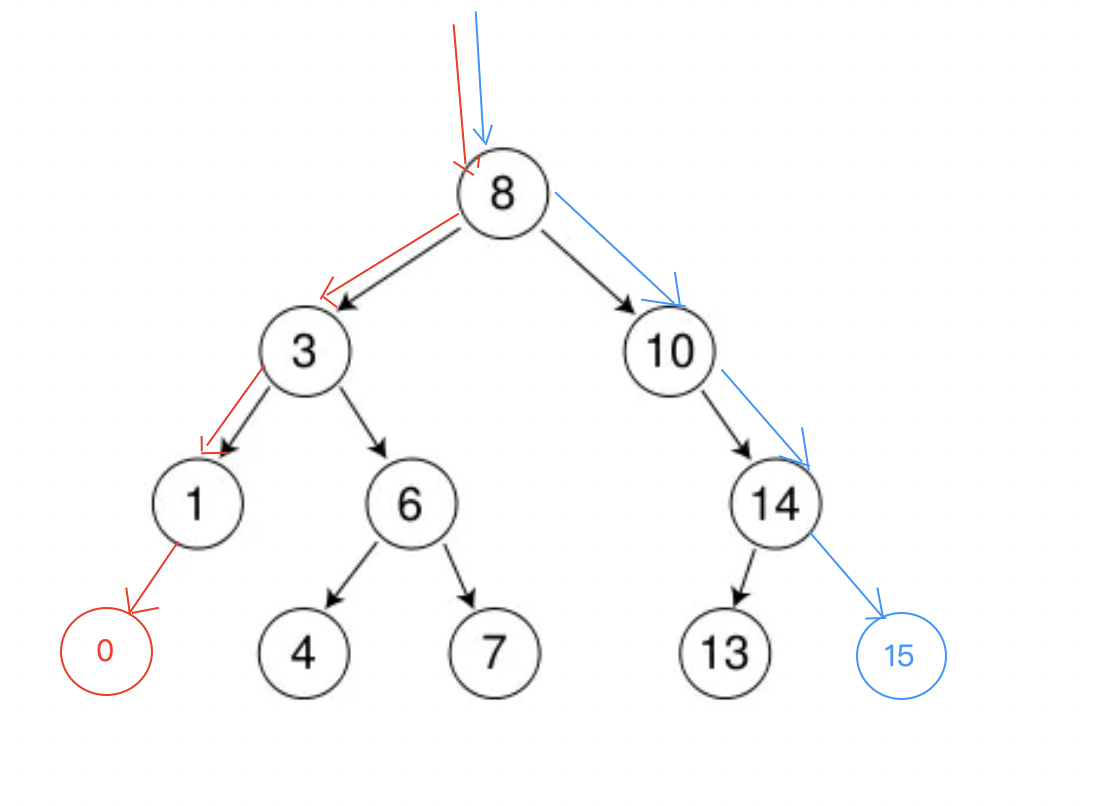
2.2、二叉搜索树的插入

  1. 若树为空则直接插入
  2. 若树不为空，按查找的性质去找查找位置

template<class K>
struct BSTreeNode {
    //typedef BSTreeNode<K> Node;

    BSTreeNode<K> *_left;
    BSTreeNode<K> *_right;
    K _key;

    BSTreeNode(const K &key) : _left(nullptr), _right(nullptr), _key(key) {}

};


template<class K>
class BinarySearchTree {
public:
    typedef BSTreeNode<K> Node;
  
		bool Insert(const K &key) {
        Node *cur = _root;
        Node *parent = nullptr;
        if (cur == nullptr) {
            Node *newNode = new Node(key);
            _root = newNode;
            return true;
        }
        while (cur) {
            if (cur->_key < key) {
                parent = cur;
                cur = cur->_right;
            } else if (cur->_key > key) {
                parent = cur;
                cur = cur->_left;
            } else {
                return false;
            }
        }

        // cur == nullptr
        Node *newNode = new Node(key);
        if (parent->_key < key)
            parent->_right = newNode;
        else if (parent->_key > key)
            parent->_left = newNode;
        return true;
    }
private:
    Node *_root = nullptr;
};

2.2、二叉树的删除

首先查找要查找的值是否在该树中，如果不存在，则返回。否则要删除的结点分下面四种情况：

  1. 要删除的结点无孩子
  2. 要删除的结点无左孩子，只有右孩子
  3. 要删除的结点无右孩子，只有左孩子
  4. 要删除的结点有左右孩子

上面1，2，3其实可以结合起来，即将要删除的结点无孩子直接归类为无左孩子（2）或者无右孩子（3）。如下：

  1. 若要删除的结点是其双亲结点的左孩子，则让其双亲的左指针指向要删除的结点的右孩子，若要删除的结点是其双亲结点的右孩子，则让其双亲的右指针指向要删除的结点的右孩子。
  2. 若要删除的结点是其双亲结点的左孩子，则让其双亲的左指针指向要删除的结点的左孩子，若要删除的结点是其双亲结点的右孩子，则让其双亲的右指针指向要删除的结点的左孩子。
  3. 找当前要删除结点的左子树中的最大值（或者右子树最小值）来替换当前结点（非递归直接赋值，递归直接交换值，仅交换值，不是交换结点）

template<class K>
struct BSTreeNode {
    //typedef BSTreeNode<K> Node;

    BSTreeNode<K> *_left;
    BSTreeNode<K> *_right;
    K _key;

    BSTreeNode(const K &key) : _left(nullptr), _right(nullptr), _key(key) {}

};


template<class K>
class BinarySearchTree {
public:
    typedef BSTreeNode<K> Node;
  
		bool Erase(const K &key) {
        Node *cur = _root;
        Node *parent = nullptr;

        if (cur == nullptr)
            return false;


        while (cur) {
            if (cur->_key < key) {
                parent = cur;
                cur = cur->_right;
            } else if (cur->_key > key) {
                parent = cur;
                cur = cur->_left;
            } else {
                //找到要删的结点

                // 当前要删的结点有一个孩子或者没有孩子
                if (cur->_left == nullptr) {
                    // 判断跟结点是否只有一颗子树
                    if (cur == _root) {
                        _root = _root->_right;
                    } else {
                        if (parent->_left == cur)
                            parent->_left = cur->_right;
                        else
                            parent->_right = cur->_right;
                    }

                    delete cur;
                    return true;

                } else if (cur->_right == nullptr) {

                    // 判断跟结点是否只有一颗子树
                    if (cur == _root) {
                        _root = _root->_left;
                    } else {
                        if (parent->_left == cur)
                            parent->_left = cur->_left;
                        else
                            parent->_right = cur->_left;
                    }


                    delete cur;
                    return true;

                } else {
                    // 当前要删的结点有两个孩子

                    // 找个替代的值去删  -- 找左子树的最右结点,即左子树最大的结点

                    Node *LeftMax = cur->_left;
                    Node *LeftMaxParent = cur;
                    while (LeftMax->_right) {
                        LeftMaxParent = LeftMax;
                        LeftMax = LeftMax->_right;
                    }

                    cur->_key = LeftMax->_key;
                    if (LeftMaxParent->_left == LeftMax)
                        LeftMaxParent->_left = LeftMax->_left;
                    else
                        LeftMaxParent->_right = LeftMax->_left;
                    delete LeftMax;
                    return true;
                }
            }
        }
        return false;
    }
private:
    Node *_root = nullptr;
};

3、二叉搜索树的实现（含递归版本）

template<class K>
struct BSTreeNode {
    //typedef BSTreeNode<K> Node;

    BSTreeNode<K> *_left;
    BSTreeNode<K> *_right;
    K _key;

    BSTreeNode(const K &key) : _left(nullptr), _right(nullptr), _key(key) {}

};


template<class K>
class BinarySearchTree {
public:
    typedef BSTreeNode<K> Node;

    BinarySearchTree() = default;

    BinarySearchTree(const BinarySearchTree<K> &b) {
        _root = Copy(b._root);
    }

    Node *Copy(Node *root) {
        if (root == nullptr)
            return nullptr;
        Node *newNode = new Node(root->_key);
        newNode->_left = Copy(root->_left);
        newNode->_right = Copy(root->_right);

        return newNode;

    }

    BinarySearchTree<K> &operator=(BinarySearchTree<K> b) {
        swap(b._root, _root);
        return *this;
    }

    ~BinarySearchTree() {
        Destroy(_root);
    }

    void Destroy(Node *root) {
        if (root == nullptr)
            return;
        Destroy(root->_left);
        Destroy(root->_right);
        delete root;
    }


    bool Erase(const K &key) {
        Node *cur = _root;
        Node *parent = nullptr;

        if (cur == nullptr)
            return false;


        while (cur) {
            if (cur->_key < key) {
                parent = cur;
                cur = cur->_right;
            } else if (cur->_key > key) {
                parent = cur;
                cur = cur->_left;
            } else {
                //找到要删的结点

                // 当前要删的结点有一个孩子或者没有孩子
                if (cur->_left == nullptr) {
                    // 判断跟结点是否只有一颗子树
                    if (cur == _root) {
                        _root = _root->_right;
                    } else {
                        if (parent->_left == cur)
                            parent->_left = cur->_right;
                        else
                            parent->_right = cur->_right;
                    }

                    delete cur;
                    return true;

                } else if (cur->_right == nullptr) {

                    // 判断跟结点是否只有一颗子树
                    if (cur == _root) {
                        _root = _root->_left;
                    } else {
                        if (parent->_left == cur)
                            parent->_left = cur->_left;
                        else
                            parent->_right = cur->_left;
                    }


                    delete cur;
                    return true;

                } else {
                    // 当前要删的结点有两个孩子

                    // 找个替代的值去删  -- 找左子树的最右结点,即左子树最大的结点

                    Node *LeftMax = cur->_left;
                    Node *LeftMaxParent = cur;
                    while (LeftMax->_right) {
                        LeftMaxParent = LeftMax;
                        LeftMax = LeftMax->_right;
                    }

                    cur->_key = LeftMax->_key;
                    if (LeftMaxParent->_left == LeftMax)
                        LeftMaxParent->_left = LeftMax->_left;
                    else
                        LeftMaxParent->_right = LeftMax->_left;
                    delete LeftMax;
                    return true;
                }
            }
        }
        return false;
    }

    bool Insert(const K &key) {
        Node *cur = _root;
        Node *parent = nullptr;
        if (cur == nullptr) {
            Node *newNode = new Node(key);
            _root = newNode;
            return true;
        }
        while (cur) {
            if (cur->_key < key) {
                parent = cur;
                cur = cur->_right;
            } else if (cur->_key > key) {
                parent = cur;
                cur = cur->_left;
            } else {
                return false;
            }
        }

        // cur == nullptr
        Node *newNode = new Node(key);
        if (parent->_key < key)
            parent->_right = newNode;
        else if (parent->_key > key)
            parent->_left = newNode;
        return true;
    }

    bool Find(const K &key) {
        Node *cur = _root;
        if (cur == nullptr)
            return false;

        while (cur) {
            if (cur->_key < key) {
                cur = cur->_right;
            } else if (cur->_key > key) {
                cur = cur->_left;
            } else {
                return true;
            }
        }

        return false;
    }

    void InOrder() {
        _InOrder(_root);
        cout << endl;
    }


    bool FindR(const K &key) {
        return _FindR(_root, key);
    }

    bool InsertR(const K &key) {
        return _InsertR(_root, key);
    }

    bool EraseR(const K &key) {
        return _EraseR(_root, key);
    }


private:

    bool _EraseR(Node *root, const K &key) {
        if (root == nullptr)
            return false;

        if (root->_key < key) {
            return _EraseR(root->_right, key);
        } else if (root->_key > key) {
            return _EraseR(root->_left, key);
        } else {

            Node *del = root;
            if (root->_right == nullptr)
                root = root->_left;
            else if (root->_left == nullptr)
                root = root->_right;
            else {
                // 将当前要删的结点的值和当前结点的左子树最大值的结点交换
                Node *LeftMax = root->_left;
                while (LeftMax->_right) {
                    LeftMax = LeftMax->_right;
                }

                swap(LeftMax->_key, root->_key);

                return _EraseR(root, key);
            }
            delete del;
            return true;
        }
    }

    bool _InsertR(Node *&root, const K &key) {
        if (root == nullptr) {
            root = new Node(key);
            return true;
        }

        if (root->_key < key) {
            return _InsertR(root->_right, key);
        } else if (root->_key > key) {
            return _InsertR(root->_left, key);
        } else {
            return false;
        }
    }

    bool _FindR(Node *root, const K &key) {
        if (root == nullptr)
            return false;

        if (root->_key < key) {
            return _FindR(root->_right, key);
        } else if (root->_key > key) {
            return _FindR(root->_left, key);
        } else {
            return true;
        }
    }


    void _InOrder(Node *root) {
        if (root == nullptr)
            return;
        if (root->_left)
            _InOrder(root->_left);
        cout << root->_key << " ";
        if (root->_right)
            _InOrder(root->_right);
    }

    Node *_root = nullptr;
};

4、二叉搜索树的应用

4.1、K模型

K模型即只有key作为关键码，结构中只需要存储key即可，关键码即为需要搜索到的值。

比如：上述实现的就是，比如存的就是整型值，看该树中是否有要查找的值。或者给一个单词word，判断该单词是否拼写正确。

4.2、KV模型

KV模型即每一个关键码key，都有与之对应的值value，即<key, value>的键值对。

比如：英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word,chinese>就构成一种键值对。

  • 对K模型的二叉搜索树进行小改造就可以得到KV模型的二叉搜索树
template<class K, class V>
    struct BSTreeNode {
        //typedef BSTreeNode<K> Node;

        BSTreeNode<K, V> *_left;
        BSTreeNode<K, V> *_right;
        K _key;
        V _val;

        BSTreeNode(const K &key,const K &val) : _left(nullptr), _right(nullptr), _key(key),_val(val) {}

    };


    template<class K, class V>
    class BinarySearchTree {
    public:
        typedef BSTreeNode<K, V> Node;

        BinarySearchTree() = default;

        BinarySearchTree(const BinarySearchTree<K, V> &b) {
            _root = Copy(b._root);
        }

        Node *Copy(Node *root) {
            if (root == nullptr)
                return nullptr;
            Node *newNode = new Node(root->_key);
            newNode->_left = Copy(root->_left);
            newNode->_right = Copy(root->_right);

            return newNode;

        }

        BinarySearchTree<K, V> &operator=(BinarySearchTree<K, V> b) {
            swap(b._root, _root);
            return *this;
        }

        ~BinarySearchTree() {
            Destroy(_root);
        }

        void Destroy(Node *root) {
            if (root == nullptr)
                return;
            Destroy(root->_left);
            Destroy(root->_right);
            delete root;
        }


        bool Erase(const K &key) {
            Node *cur = _root;
            Node *parent = nullptr;

            if (cur == nullptr)
                return false;


            while (cur) {
                if (cur->_key < key) {
                    parent = cur;
                    cur = cur->_right;
                } else if (cur->_key > key) {
                    parent = cur;
                    cur = cur->_left;
                } else {
                    //找到要删的结点

                    // 当前要删的结点有一个孩子或者没有孩子
                    if (cur->_left == nullptr) {
                        // 判断跟结点是否只有一颗子树
                        if (cur == _root) {
                            _root = _root->_right;
                        } else {
                            if (parent->_left == cur)
                                parent->_left = cur->_right;
                            else
                                parent->_right = cur->_right;
                        }

                        delete cur;
                        return true;

                    } else if (cur->_right == nullptr) {

                        // 判断跟结点是否只有一颗子树
                        if (cur == _root) {
                            _root = _root->_left;
                        } else {
                            if (parent->_left == cur)
                                parent->_left = cur->_left;
                            else
                                parent->_right = cur->_left;
                        }


                        delete cur;
                        return true;

                    } else {
                        // 当前要删的结点有两个孩子

                        // 找个替代的值去删  -- 找左子树的最右结点,即左子树最大的结点

                        Node *LeftMax = cur->_left;
                        Node *LeftMaxParent = cur;
                        while (LeftMax->_right) {
                            LeftMaxParent = LeftMax;
                            LeftMax = LeftMax->_right;
                        }

                        cur->_key = LeftMax->_key;
                        if (LeftMaxParent->_left == LeftMax)
                            LeftMaxParent->_left = LeftMax->_left;
                        else
                            LeftMaxParent->_right = LeftMax->_left;
                        delete LeftMax;
                        return true;
                    }
                }
            }
            return false;
        }

        bool Insert(const K &key,const K &val) {
            Node *cur = _root;
            Node *parent = nullptr;
            if (cur == nullptr) {
                Node *newNode = new Node(key,val);
                _root = newNode;
                return true;
            }
            while (cur) {
                if (cur->_key < key) {
                    parent = cur;
                    cur = cur->_right;
                } else if (cur->_key > key) {
                    parent = cur;
                    cur = cur->_left;
                } else {
                    return false;
                }
            }

            // cur == nullptr
            Node *newNode = new Node(key,val);
            if (parent->_key < key)
                parent->_right = newNode;
            else if (parent->_key > key)
                parent->_left = newNode;
            return true;
        }

        Node *Find(const K &key) {
            Node *cur = _root;
            if (cur == nullptr)
                return nullptr;

            while (cur) {
                if (cur->_key < key) {
                    cur = cur->_right;
                } else if (cur->_key > key) {
                    cur = cur->_left;
                } else {
                    return cur;
                }
            }

            return nullptr;
        }

        void InOrder() {
            _InOrder(_root);
            cout << endl;
        }


    private:

        void _InOrder(Node *root) {
            if (root == nullptr)
                return;
            if (root->_left)
                _InOrder(root->_left);
            cout << root->_key << " ";
            if (root->_right)
                _InOrder(root->_right);
        }

        Node *_root = nullptr;
    };

void test_BST_KV() {
    BinarySearchTree<string, string> bstkv;
    bstkv.Insert("hello", "你好");
    bstkv.Insert("xp", "徐鹏");
    bstkv.Insert("zl", "紫玲");
    bstkv.Insert("search", "搜索");
    string s;
    while (cin >> s) {
        auto ret = bstkv.Find(s);
        if (ret)
            cout << ret->_val << endl;
        else
            cout << "没有这个" << endl;
    }
}

5、二叉搜索树的性能分析

由于二叉搜索树的插入和删除都用到了查找，所以查找效率代表了二叉搜索树的各操作的性能。

对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，深度越深，查找中比较的次数越多。

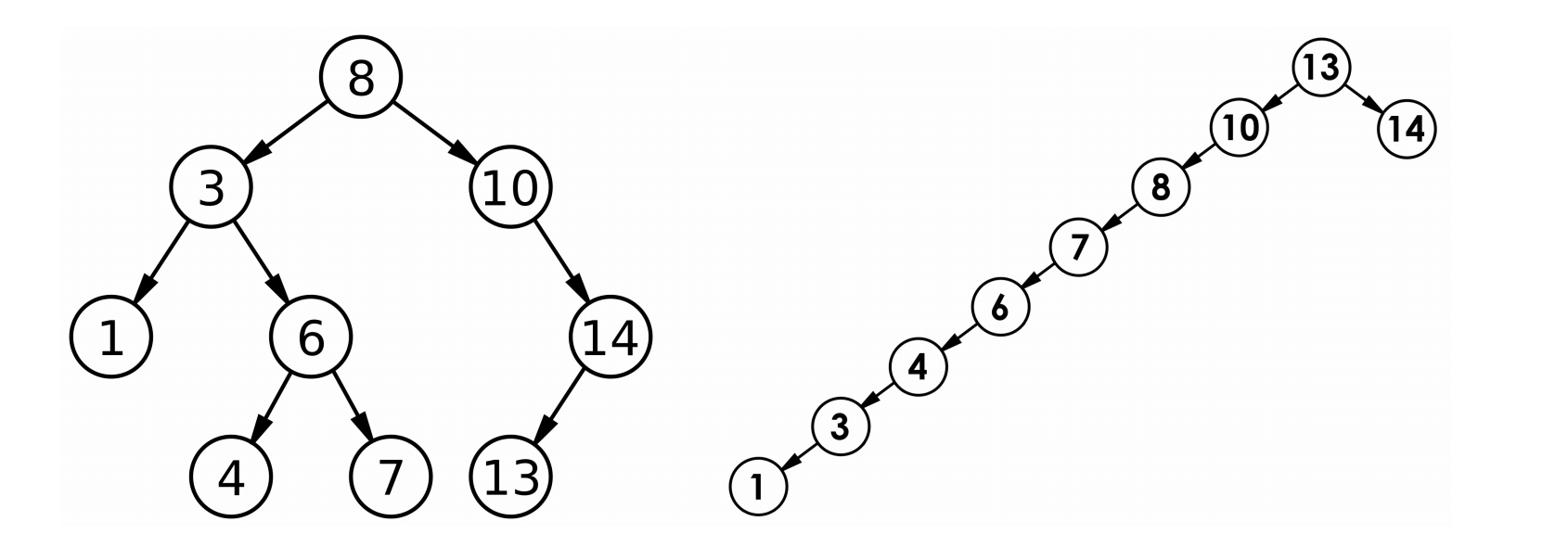
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树。

时间复杂度：

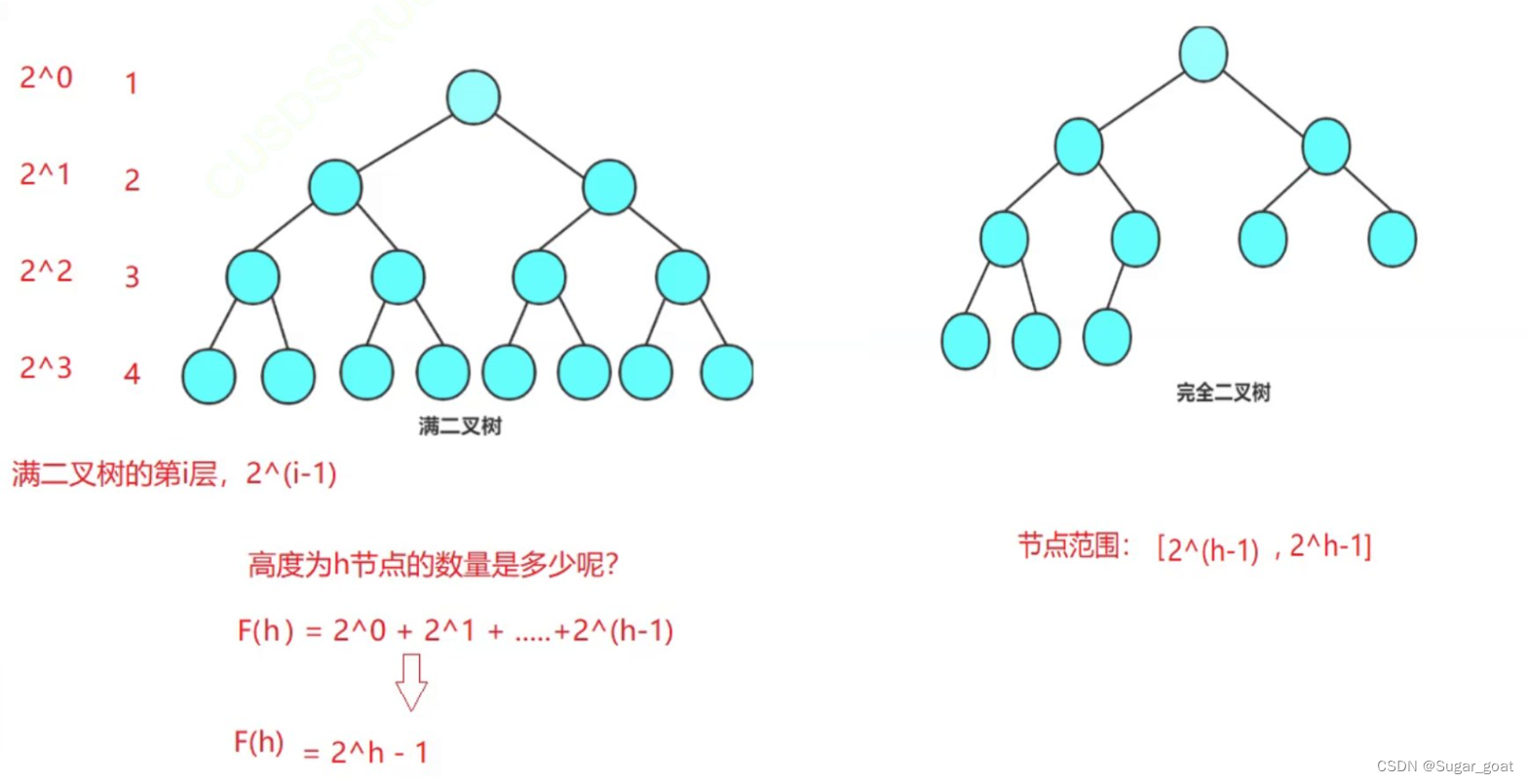
  1. 在最优的情况下，二叉搜索树接近为完全二叉树，其平均比较次数为：nlogn
  2. 在最坏的情况下，二叉搜索树接近为单边二叉树，其平均比较次数为：n^2

如果退化为单边树，那么二叉搜索树的优势就失去了，怎么解决？后面学了AVL（平衡二叉树）和红黑树就可以解决这个问题。

6、二叉树进阶面试题

1、606. 根据二叉树创建字符串

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 606. 根据二叉树创建字符串

class Solution {
public:


    string tree2str(TreeNode *root) {
        if (root == nullptr)
            return "";

        string str = to_string(root->val);

        // 要加括号：1、当前结点的左不空,左为空右不空也要加
        //         2、当前结点的右不空

        // 往左子树找
        if (root->left || root->right) {
            str += '(';
            str += tree2str(root->left);
            str += ')';
        }

        // 往右子树找
        if (root->right) {
            str += '(';
            str += tree2str(root->right);
            str += ')';
        }

        return str;
    }
};

2、102. 二叉树的层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 102. 二叉树的层序遍历
class Solution {
public:
    vector <vector<int>> levelOrder(TreeNode *root) {
        vector <vector<int>> vv;
        if (root == nullptr)
            return vv;

        queue < TreeNode * > q;
        q.push(root);

        while (!q.empty()) {
            vector<int> v; // 用来每次尾插vv
            int size = q.size();// 当前层的元素个数
            for (int i = 0; i < size; ++i) {
                TreeNode *cur = q.front();
                v.push_back(cur->val);
                q.pop();
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
            }
            vv.push_back(v);
        }

        return vv;
    }
};

3、107. 二叉树的层序遍历 II

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 107. 二叉树的层序遍历 II
class Solution {
public:
    vector <vector<int>> levelOrderBottom(TreeNode *root) {
        vector <vector<int>> vv;
        if (root == nullptr)
            return vv;

        queue < TreeNode * > q;
        q.push(root);

        while (!q.empty()) {
            vector<int> v; // 用来每次尾插vv
            int size = q.size();// 当前层的元素个数
            for (int i = 0; i < size; ++i) {
                TreeNode *cur = q.front();
                v.push_back(cur->val);
                q.pop();
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
            }
            vv.push_back(v);
        }

        reverse(vv.begin(),vv.end());
        return vv;
    }
};

4、236. 二叉树的最近公共祖先

  • 解法一：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    bool IsInTree(TreeNode *root, TreeNode *cur) {
        if (root == nullptr)
            return false;
        return root == cur || IsInTree(root->left, cur) || IsInTree(root->right, cur);
    }

    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {

        if (root == nullptr)
            return nullptr;

        if (p == root || q == root)
            return root;

        bool pInLeft, pInRight, qInLeft, qInRight;

        pInLeft = IsInTree(root->left, p);
        pInRight = !pInLeft; // p肯定在左右子树中的一个

        qInLeft = IsInTree(root->left, q);
        qInRight = !qInLeft; // q肯定在左右子树中的一个

        if ((pInLeft && qInRight) || (pInRight && qInLeft)) {
            // 左右子树各一个，那么当前结点就是公共结点
            return root;
        } else if ((pInLeft && qInLeft)) {
            return lowestCommonAncestor(root->left, p, q);// 去左子树找
        } else
            return lowestCommonAncestor(root->right, p, q);// 去右子树找
    }
};
  • 解法二：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */


//  236. 二叉树的最近公共祖先
class Solution {
public:

    bool GetPath(TreeNode *root, TreeNode *cur, stack<TreeNode *> &v) {

        if (root == nullptr)
            return false;

        v.push(root);

        if (cur == root)
            return true;

        // 去左边找
        if (GetPath(root->left, cur, v))
            return true;

        // 去右边找
        if (GetPath(root->right, cur, v))
            return true;

        // 左右都没找到
        v.pop();
        return false;
    }

    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {

        stack < TreeNode * > sp;
        stack < TreeNode * > sq;
        GetPath(root, p, sp);
        GetPath(root, q, sq);

        // 两个路径找交点
        while (sp.size() != sq.size()) {
            if (sp.size() > sq.size())
                sp.pop();
            else
                sq.pop();
        }

        while (sp.top() != sq.top()) {
            sp.pop();
            sq.pop();
        }

        return sp.top();
    }
};

5、JZ36 二叉搜索树与双向链表

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/

// JZ36 二叉搜索树与双向链表
class Solution {
public:

    void InOrderConvert(TreeNode *cur, TreeNode *&pre) {
        if (cur == nullptr)
            return;

        InOrderConvert(cur->left, pre);

        // 关键
        cur->left = pre;

        if (pre)
            pre->right = cur;

        pre = cur;

        InOrderConvert(cur->right, pre);

    }

    TreeNode *Convert(TreeNode *pRootOfTree) {
        if (!pRootOfTree)
            return nullptr;
        TreeNode *pre = nullptr;
        InOrderConvert(pRootOfTree, pre);

        TreeNode *head = pRootOfTree;
        while (head->left) {
            head = head->left;
        }

        return head;
    }

};

6、105. 从前序与中序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 105. 从前序与中序遍历序列构造二叉树
class Solution {
public:

    TreeNode *_buildTree(vector<int> &preorder, vector<int> &inorder, int &prei, int inbegin, int inend) {
        //   中序左右区间不对
        if (inbegin > inend)
            return nullptr;

        // 先创建结点 ，再构建它的左右子树
        TreeNode *root = new TreeNode(preorder[prei++]);

        // 中序序列划分左右区间
        int rooti = inbegin;
        while (rooti <= inend) {
            if (inorder[rooti] != root->val)
                rooti++;
            else
                break;
        }

        // 再构建左右子树
        // [inbegin,rooti-1]  [rooti+1,inend]
        root->left = _buildTree(preorder, inorder, prei, inbegin, rooti - 1);
        root->right = _buildTree(preorder, inorder, prei, rooti + 1, inend);

        return root;
    }

    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        int prei = 0;
        return _buildTree(preorder, inorder, prei, 0, inorder.size() - 1);
    }
};

7、106. 从中序与后序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 106. 从中序与后序遍历序列构造二叉树
class Solution {
public:

    TreeNode *_buildTree(vector<int> &inorder, vector<int> &postorder, int &posti, int inbegin, int inend) {
        //   中序左右区间不对
        if (inbegin > inend)
            return nullptr;

        // 先创建结点 ，再构建它的左右子树
        TreeNode *root = new TreeNode(postorder[posti--]);

        // 中序序列划分左右区间 先构建右子树
        int rooti = inend;
        while (rooti >= inbegin) {
            if (inorder[rooti] != root->val)
                rooti--;
            else
                break;
        }

        // 再构建右左子树
        // [inbegin,rooti-1]  [rooti+1,inend]
        root->right = _buildTree(inorder, postorder, posti, rooti + 1, inend);
        root->left = _buildTree(inorder, postorder, posti, inbegin, rooti - 1);

        return root;
    }

    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {
        int posti = postorder.size() - 1;
        return _buildTree(inorder, postorder, posti, 0, inorder.size() - 1);
    }
};

8、144. 二叉树的前序遍历

  • 用非递归方法：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 144. 二叉树的前序遍历
class Solution {
public:
    vector<int> preorderTraversal(TreeNode *root) {
        stack < TreeNode * > s;
        vector<int> v;

        TreeNode *cur = root;

        while (cur || !s.empty()) {

            while (cur) {
                v.push_back(cur->val);
                s.push(cur);
                cur = cur->left;
            }

            // 左子树已经走完
            TreeNode *top = s.top();
            s.pop();

            // 现在走右子树
            cur = top->right;
        }

        return v;
    }
};

9、94. 二叉树的中序遍历

  • 用非递归方法：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 94. 二叉树的中序遍历
class Solution {
public:
    vector<int> inorderTraversal(TreeNode *root) {
        stack < TreeNode * > s;
        vector<int> v;

        TreeNode *cur = root;

        while (cur || !s.empty()) {

            while (cur) {
                s.push(cur);
                cur = cur->left;
            }

            // 左子树已经走完
            TreeNode *top = s.top();
            s.pop();

            // 出栈的时候访问
            v.push_back(top->val);
            // 现在走右子树
            cur = top->right;
        }

        return v;
    }
};

10、145. 二叉树的后序遍历

  • 用非递归方法：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 145. 二叉树的后序遍历
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        stack < TreeNode * > s;
        vector<int> v;

        TreeNode *cur = root;
        TreeNode *pre = nullptr;

        while (cur || !s.empty()) {

            while (cur) {
                s.push(cur);
                cur = cur->left;
            }

            // 左子树已经走完
            TreeNode *top = s.top();

            // 当前结点的右子树为空，可以访问当前结点
            // 或者右子树不空，但是已经访问过，也可以访问当前结点
            // 否则去右子树继续访问
            if (top->right == nullptr || top->right == pre) {
                v.push_back(top->val);
                s.pop();
              	// top被pop掉了说明top就变成上一个被访问的结点
                pre = top;
            } else {
                // 现在走右子树
                cur = top->right;
            }
        }

        return v;
    }
};

OKOK，二叉排序树的讲解就到这里。如果你对Linux和C++也感兴趣的话，可以看看我的主页哦。下面是我的github主页，里面记录了我的学习代码和leetcode的一些题的题解，有兴趣的可以看看。

Xpccccc的github主页

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1534574.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

5.MySQL创建表单和用户

5.MySQL创建表单和用户

1.数据库的创建 2.创建表单 3.创建用户 创建好用户之后&#xff0c;让用户只能访问一个表的权限 再创建一个数据库&#xff0c;用户名是刚刚创建的用户&#xff0c;密码是自己设置的密码&#xff0c;这样就缩小了权限。
阅读更多...
2024.3.21

2024.3.21

qt实现登录界面 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this);//设置纯净窗口this->setWindowFlag(Qt::FramelessWindowHint);/…
阅读更多...
电影aac是什么意思？如何播放、转换、编辑aac？

电影aac是什么意思？如何播放、转换、编辑aac？

"电影AAC"这个术语可能是指电影中的音频编码格式。AAC&#xff08;Advanced Audio Coding&#xff09;是一种常见的音频编码格式&#xff0c;通常用于压缩音频文件&#xff0c;以在保持高质量的同时减小文件大小。在电影中&#xff0c;AAC格式的音频通常用于提供高质…
阅读更多...
深入解析Mybatis-Plus框架：简化Java持久层开发(十二)

深入解析Mybatis-Plus框架：简化Java持久层开发(十二)

&#x1f340; 前言 博客地址&#xff1a; CSDN&#xff1a;https://blog.csdn.net/powerbiubiu &#x1f44b; 简介 本章节介绍如何通过Mybatis-Plus进行实现批量新增。 &#x1f4d6; 正文 1 为何要批量插入&#xff1f; 前面章节已经介绍&#xff0c;Mapper接口只有一个…
阅读更多...
那些场景需要额外注意线程安全问题

那些场景需要额外注意线程安全问题

主要学习那些场景需要额外注意线程安全问题&#xff0c;在这里总结了四中场景。 访问共享变量或资源 第一种场景是访问共享变量或共享资源的时候&#xff0c;典型的场景有访问共享对象的属性&#xff0c;访问static静态变量&#xff0c;访问共享的缓存&#xff0c;等等。因为…
阅读更多...
React 系列 之 React Hooks（一） JSX本质、理解Hooks

React 系列 之 React Hooks（一） JSX本质、理解Hooks

借鉴自极客时间《React Hooks 核心原理与实战》 JSX语法的本质 可以认为JSX是一种语法糖&#xff0c;允许将html和js代码进行结合。 JSX文件会通过babel编译成js文件 下面有一段JSX代码&#xff0c;实现了一个Counter组件 import React from "react";export defau…
阅读更多...
【机器学习】深入解析线性回归模型

【机器学习】深入解析线性回归模型

&#x1f388;个人主页&#xff1a;豌豆射手^ &#x1f389;欢迎 &#x1f44d;点赞✍评论⭐收藏 &#x1f917;收录专栏&#xff1a;机器学习 &#x1f91d;希望本文对您有所裨益&#xff0c;如有不足之处&#xff0c;欢迎在评论区提出指正&#xff0c;让我们共同学习、交流进…
阅读更多...
原创！分解+集成思想新模型！VMD-CNN-BiGRU-Attention一键实现时间序列预测！以风速数据集为例

原创！分解+集成思想新模型！VMD-CNN-BiGRU-Attention一键实现时间序列预测！以风速数据集为例

声明&#xff1a;文章是从本人公众号中复制而来&#xff0c;因此&#xff0c;想最新最快了解各类智能优化算法及其改进的朋友&#xff0c;可关注我的公众号&#xff1a;强盛机器学习&#xff0c;不定期会有很多免费代码分享~ 目录 数据介绍 模型流程 创新点 结果展示 部…
阅读更多...
【背诵】全国计算机等级考试一级网络安全素质教育考试【填空题】建议收藏

【背诵】全国计算机等级考试一级网络安全素质教育考试【填空题】建议收藏

背诵记忆稳拿20分 180道填空题&#xff0c;背会即拿20分
阅读更多...
【系统架构设计师】计算机系统基础知识 03

【系统架构设计师】计算机系统基础知识 03

系统架构设计师 - 系列文章目录 01 系统工程与信息系统基础 02 软件架构设计 03 计算机系统基础知识 文章目录 系统架构设计师 - 系列文章目录 文章目录 前言 一、计算机系统概述 1.计算机组成 ​编辑2.存储系统 二、操作系统 ★★★★ 1.进程管理 2.存储管理 1.页式存储 …
阅读更多...
Java：设计模式

Java：设计模式

文章目录 参考简介工厂模式简单工厂模式工厂方法模式抽象工厂模式总结 单例模式预加载懒加载线程安全问题 策略模式 参考 知乎 简介 总体来说设计模式分为三类共23种。 创建型模式&#xff0c;共五种&#xff1a;工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模…
阅读更多...
Java 22正式发布，一文了解全部新特性

Java 22正式发布，一文了解全部新特性

就在昨晚&#xff0c;Java 22正式发布&#xff01;该版本提供了 12 项功能增强&#xff0c;其中包括 7 项预览功能和 1 项孵化器功能。它们涵盖了对 Java 语言、API、性能以及 JDK 中包含的工具的改进。 下面就来一起学习一下该版本都更新了哪些新特性&#xff01; Unnamed V…
阅读更多...
世媒讯软文营销策略如何做才能达到引流的目的

世媒讯软文营销策略如何做才能达到引流的目的

软文营销是一种通过撰写软文来宣传企业、产品或服务的网络营销方式。通过撰写具有故事性、吸引人的文章来间接推广产品、服务或品牌的营销策略。要实现软文营销的目的&#xff0c;即引流&#xff08;吸引流量&#xff09;&#xff0c;以下是一些有效的策略&#xff1a; 新闻策略…
阅读更多...
学点儿Java_Day7_继承、重载、重写、多态、抽象类

学点儿Java_Day7_继承、重载、重写、多态、抽象类

1 继承 1.1 概念与理解 继承&#xff1a; 你继承谁你就是谁&#xff0c;继承是一种严格的父子关系&#xff08;抽取到父类里面的属性和方法一定是所有子类所共有&#xff09;      &#xff08;Student继承Person&#xff0c;那么Student就是人&#xff09; 面向对象特征…
阅读更多...
数据结构：初识树和二叉树

数据结构：初识树和二叉树

目前主流的方式是左孩子右兄弟表示法 我们的文件系统就是一个树 以上就是树的概念&#xff0c;我们今天还要来学习一种从树演变的重要的结构&#xff1a;二叉树 顾名思义二叉树就是一个结点最多有两个子树。 其中我们还要了解满二叉树和完全二叉树的概念 注意我们的完全二叉…
阅读更多...
四、C语言中的数组：如何输入与输出二维数组（数组，完）

四、C语言中的数组：如何输入与输出二维数组（数组，完）

本章的学习内容如下 四、C语言中的数组&#xff1a;数组的创建与初始化四、C语言中的数组&#xff1a;数组的输入与元素个数C语言—第6次作业—十道代码题掌握一维数组四、C语言中的数组&#xff1a;二维数组 1.二维数组的输入与输出 当我们输入一维数组时需要一个循环来遍历…
阅读更多...
10.注册页面

10.注册页面

注册页面 在pages中新建页面register 复制粘贴之前的登录页面 设置上传头像图片 微信官方文档 https://developers.weixin.qq.com/miniprogram/dev/framework/open-ability/userProfile.html <button class"avatar-wrapper" open-type"chooseAvatar&quo…
阅读更多...
微调alpaca-lora遇到的一些问题

微调alpaca-lora遇到的一些问题

1、环境简介 环境&#xff1a; 系统&#xff1a;Ubuntu torch&#xff1a;2.2.1 python&#xff1a;3.10 gpu&#xff1a;V100 16g peft&#xff1a;0.9.0 使用PEFT中的lora方式微调llama-2-7b-hf&#xff0c;项目地址&#xff1a;alpaca-lora 2、混合精度训练Tensor相互计算会…
阅读更多...
海外重要行业媒体：知名服务商IntoTheBlock现已集成波场TRON网络分析数据

海外重要行业媒体：知名服务商IntoTheBlock现已集成波场TRON网络分析数据

近日,领先链上分析服务提供商 IntoTheBlock 宣布已将波场 TRON 网络集成至其市场情报套件。该合作引发多家海外加密媒体关注,Crypto Slate、Crypto Briefing等均对此进行了报道,称此次合作意义深远,能帮助数百万用户更深入地了解波场TRON生态系统。 报道表示,波场TRON网络规模大…
阅读更多...
中文编程入门（Lua5.4.6中文版）第十一章 Lua 模块与包 参考星争际霸游戏

中文编程入门（Lua5.4.6中文版）第十一章 Lua 模块与包 参考星争际霸游戏

在遥远的星争际霸世界中&#xff0c;代码模块就如同星际基地中的高科技仓库&#xff0c;储存着各类经过封装优化的战术指令和战略资源。自Lua 5.1版本起&#xff0c;星际编程者们引入了标准化的模块管理系统&#xff0c;使得不同战舰之间能够共享和调用核心战斗算法&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023