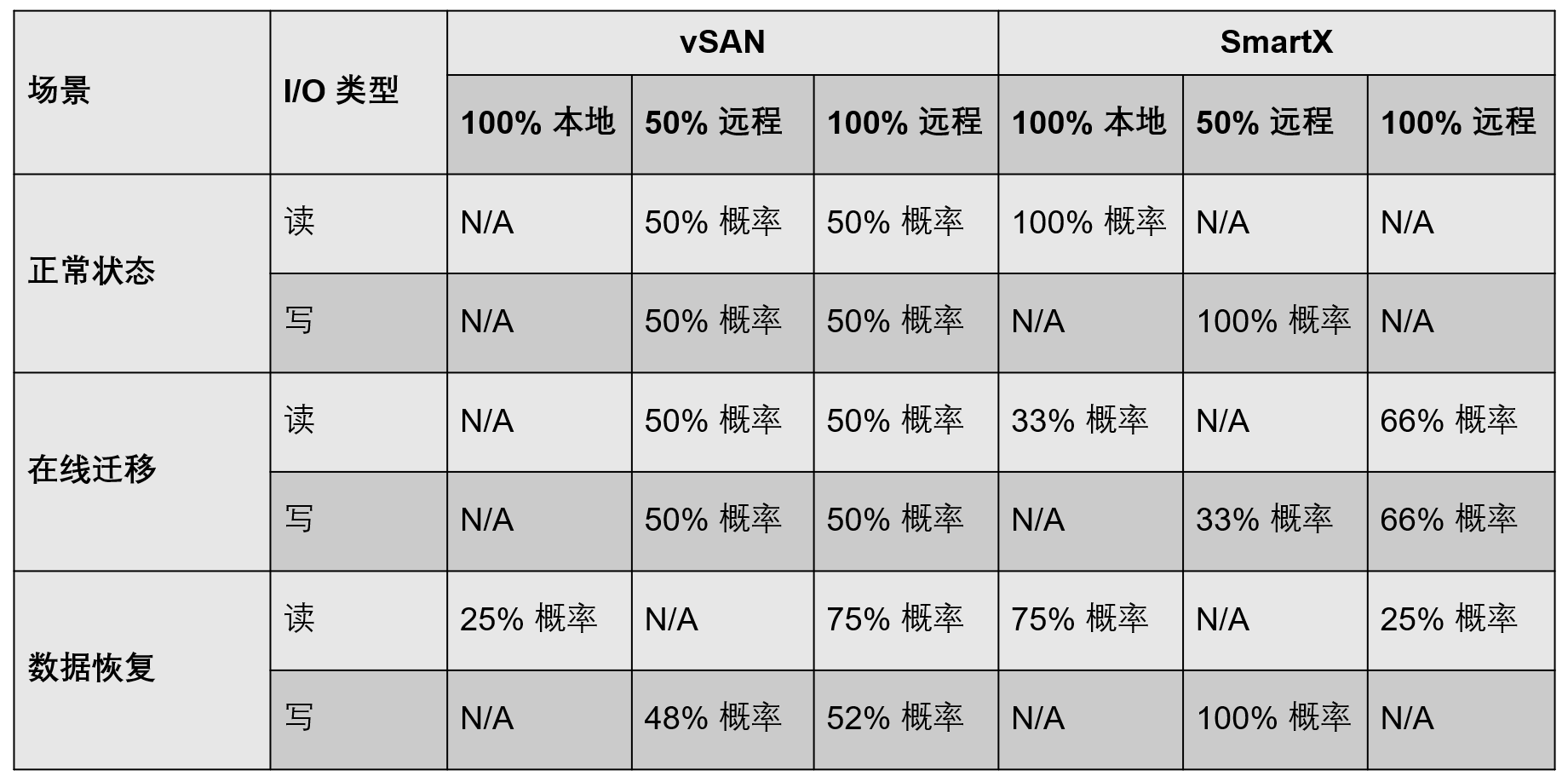
[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第39讲。

报数游戏，本题是2020年8月23日举办的第12届蓝桥杯青少组Python编程选拔赛真题。题目要求编程实现报数游戏，n个人围成一圈，从第一个人开始从1报道3，报3的人退出圈子，直到最后一个人游戏结束，计算出最后留下的是原来的第几号。

先来看看题目的要求吧。

一.题目说明

编程实现：

有n个人围成一个圈，按顺序排好号。然后从第一个人开始报数（从1到3报数），报到3的人退出圈子，然后继续从1到3报数，直到最后留下一个人游戏结束，问最后留下的是原来第几号。

输入描述：

输入一个正整数n

输出描述：

输出最后留下的是原来的第几号

样例输入：

5

样例输出：

4

评分标准：

• 3分：能正确输出一组数据

• 5分：能正确输出两组数据；

• 7分：能正确输出三组数据；

• 10分：能正确输出四组数据。

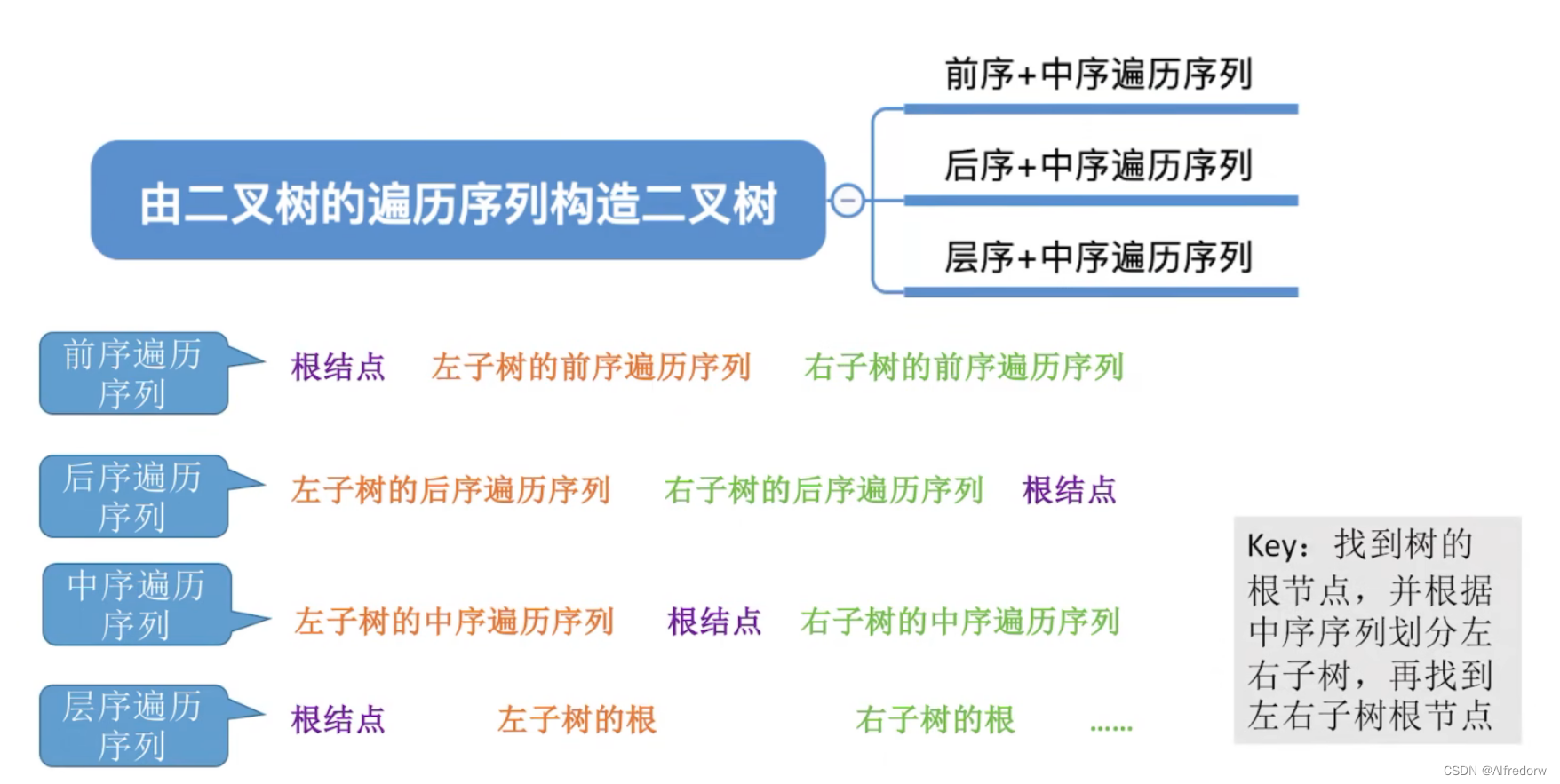
二.思路分析

这是一道经典的约瑟夫环问题，有多种不同的解决方案，涉及的知识点也有所不同，但基本上都会用到列表和循环。

据说著名犹太历史学家Josephus经历过这样的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人宁愿死也不想被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。

然而Josephus和他的朋友并不想遵从，于是就先假装遵从，Josephus将朋友与自己安排在第16个与第31个位置。这样当所有犹太人全部自杀后，他和他的朋友就逃过了这场死亡游戏。

这个故事可以看作是约瑟夫问题的由来，通常描述为：N个人围成一圈，第一个人从1开始依次进行报数，当报到M时将该人杀掉。然后从被杀掉的下一个人开始，重新从1继续报数，直到只剩下最后一个人，试问最终存活下来的人是谁？

为了帮助你更好的理解这个过程，我们假定有6个人排队，从第一个人开始报数，每次数到2的人出列，初始情况如图所示：

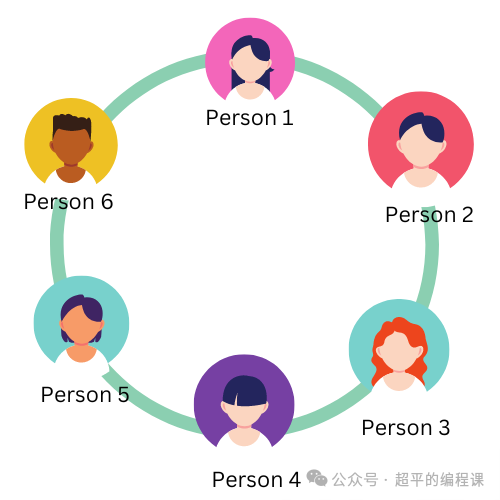
从第一个人开始报数，Person1报1，Person2报2，因此Person2出列，如图：

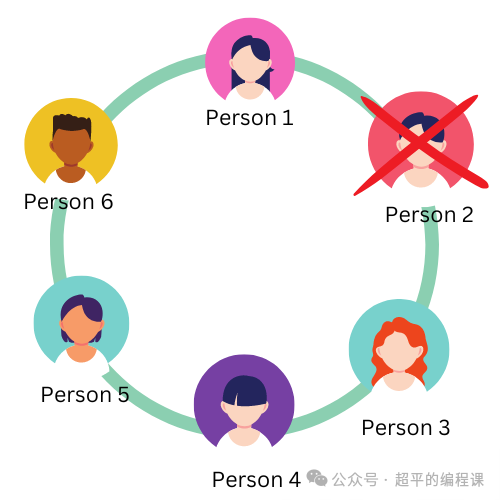
接下来Person3又从1开始报数，Person4报2，因此Person4出列，如图：

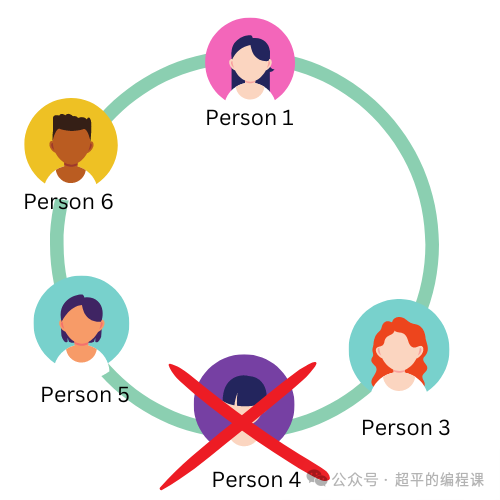
然后Person5继续从1开始报数，Person6报2，因此Person6出列，如图：

转了一圈，又回到Person1了，Person1报1，Person3报2，因此Person3出列，如图：

最后轮到Person5报1了，Person1报2，因此Person1出列，如图：

因此，最后的胜利者是Person5。

针对约瑟夫问题，常见的解决方案包括列表模拟算法、循环链表法、队列法、递归算法、递推算法和动态规划算法等。

为简单起见，我们先从最简单的模拟算法入手，使用列表保存这n个人的状态，其中1表示在列，0表示已出列，列表项索引则表示每个人的编号（需要加1），如下：

people = [1, 1, 1, 1, 1, 1,...,1]

刚开始所有人在列，每一项都为1，接下来从从头开始遍历列表，模拟报数过程，如下：

1). 如果当前列表项people[i]为1，说明还在列，就报数，如果当前列表项为0，说明已出列，不做任何操作；

2). 每一个在列的人报完数，需要将数字增加1，如果数字为4，则重置为1；

3). 报数时，如果数字为3，则需要出列，只需要将people[i]设置为0即可；

4). 当列表遍历完成后，需要再回到列表头部，重复上述过程；

5). 当列表中只有一项为1时，循环结束。

一旦你理解了列表模拟算法，我们可以借助队列简化这个过程，之所以选择队列，是因为Python在collections标准库中提供了队列容器，使用起来非常方便。

所谓队列，是指一种特殊的列表，其特殊之处在于它只允许队头进行删除操作，通常称为出队，而在队尾进行插入操作，通常称为入队。

像队列这种最先进去的数据最先被取来，即“先进先出”的结构，我们称为First In First Out，简称FIFO。

这和我们日常生活中排队的现象如出一辙，所以称作队列。

队列又分为单向队列（queue）和双端队列（deque），二者的区别就在于前者只能在队头删除和队尾插入，而后者则可以在任何一端进行删除和插入操作，我们要使用的是双端队列。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们使用两种方法来编写程序：

• 列表模拟算法

• 队列模拟算法

1. 列表模拟算法

根据前面的思路分析，我们编写代码如下：

代码不多，简单说明3点：

1). 列表提供了count()方法，用于统计指定内容的数量，只要1的数量 > 1，就要继续报数；

2). i表示索引，当i = n时，表示列表已经遍历完了，需要将i重置为0，可以使用取模运算实现，即 i = （i + 1）% n ，当然你也可以使用if...else语句来实现；

3). 最后只有一项为1，通过列表的index()方法，获取其索引，由于列表索引是从0开始的，因此需要加1，才是最后一个人的正确编号。

2. 队列模拟算法

根据前面的思路分析，编写代码如下：

代码比较简单，关键在于理解其过程和各代码的作用，说明如下：

1). 这里的deque是双端队列，支持从两端添加和删除元素。

2). deque()方法用于初始化队列，此处使用了range()函数，得到的队列和列表结构一样，如下：

people = [1, 2, 3, 4, 5, ... , n]

3). 这里的rotate(-1)是关键，它的作用是将队列的队头元素移动到队尾，而其它的元素则相应地向左移动一位。

假设n = 5，初始队列如下：

[1, 2, 3, 4, 5]

第一次调用rotate(-1)方法，将队头的1移到队尾，其它的则左移了一位，如下：

[2, 3, 4, 5, 1]

第二次调用rotate(-1)方法，将队头的2移到队尾，其它的左移一位，如下：

[3, 4, 5, 1, 2]

如此一来，就将需要删除的3移到队头了。

4). for循环的作用就是将每次报到3的元素移到队头，然后使用popleft()函数删除队头元素。

如此重复上述过程，当整个队列只剩下一个元素时，结束循环，这个元素就是最后一个人的编号。

至此，整个程序就全部完成了，你也可以输入不同的数字来测试效果。

四.总结与思考

本题代码在15行左右，涉及到的知识点包括：

• 循环语句，包括while循环和for信号；

• 条件语句及其嵌套用法；

• 列表的常见方法；

• 列表推导式的用法；

从知识点的层面上来讲，都是大家比较熟悉的内容，本题的关键在于充分理解报数的过程，理顺其中的逻辑关系，然后使用列表结合循环来模拟这个过程。

当然，如果对循环链表和队列有所了解的话，借助这些数据结构，可以极大地简化代码。

Python中的列表是一种动态数组，支持在列表的任意位置进行插入、删除和访问元素，类似于链表的灵活性。在大部分情况下，Python的列表已经能够满足链表的需求，因此没有提供链表这种数据结构。

队列分为单向队列和双端队列，其区别在于前者只能在队头进行删除操作、在队尾进行插入操作，而后者在队头和队尾都可以进行插入、删除操作。

在Python中，可以使用列表来模拟单向队列，因而collections模块没有提供单向队列的实现。而双端队列支持从两端添加和删除元素的操作的特性使得它在某些算法和数据结构处理中非常灵活和高效，为此，collections模块专门提供了双端队列deque。

当然，除了上面给出的两种解法，还可以使用递归、递推和动态规划等算法来实现，其代码更为简洁，但是理解起来有些难度，超平老师会在后续的教程中专门讲解，敬请期待。

超平老师给你留一道思考题，本题中的3是固定的，如果它也是变化的，不妨用m来表示，又该如何实现呢？

你还有什么好的想法和创意吗，也非常欢迎和超平老师分享探讨。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香😄

需要源码的，可以移步至“超平的编程课”gzh。