目录
1、扫雷(Google Kickstart2014 Round C Problem A)
2、动态网格(Google Kickstart2015 Round D Problem A)
3、走迷宫(模板)
4、画图(第六次CCF计算机软件能力认证)
5、山峰和山谷(POI2007 & 《信息学奥赛一本通》)
1、扫雷(Google Kickstart2014 Round C Problem A)
扫雷是一种计算机游戏,在 20 世纪 80 年代开始流行,并且仍然包含在某些版本的 Microsoft Windows 操作系统中。
在这个问题中,你正在一个矩形网格上玩扫雷游戏。
最初网格内的所有单元格都呈未打开状态。
其中 M 个不同的单元格中隐藏着 M 个地雷。
其他单元格内不包含地雷。
你可以单击任何单元格将其打开。
如果你点击到的单元格中包含一个地雷,那么游戏就会判定失败。
如果你点击到的单元格内不含地雷,则单元格内将显示一个 0 到 8 之间的数字(包括 0 和 8),这对应于该单元格的所有相邻单元格中包含地雷的单元格的数量。
如果两个单元格共享一个角或边,则它们是相邻单元格。
另外,如果某个单元格被打开时显示数字 0,那么它的所有相邻单元格也会以递归方式自动打开。
当所有不含地雷的单元格都被打开时,游戏就会判定胜利。
例如,网格的初始状态可能如下所示(* 表示地雷,而 c 表示第一个点击的单元格):
*..*...**.
....*.....
..c..*....
........*.
..........
被点击的单元格旁边没有地雷,因此当它被打开时显示数字 00,并且它的 88 个相邻单元也被自动打开,此过程不断继续,最终状态如下:
*..*...**.
1112*.....
00012*....
00001111*.
00000001..
此时,仍有不包含地雷的单元格(用 . 字符表示)未被打开,因此玩家必须继续点击未打开的单元格,使游戏继续进行。
你想尽快赢得游戏胜利并希望找到赢得游戏的最低点击次数。
给定网格的尺寸(N×N),输出能够获胜的最小点击次数。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 N,表示游戏网格的尺寸大小。
接下来 N 行,每行包含一个长度为 N 的字符串,字符串由 .(无雷)和 *(有雷)构成,表示游戏网格的初始状态。
输出格式
每组数据输出一个结果,每个结果占一行。
结果表示为 Case #x: y,其中 x 是组别编号(从 1 开始),y 是获胜所需的最小点击次数。
数据范围
1≤T≤100
1≤N≤300
输入样例:
2
3
..*
..*
**.
5
..*..
..*..
.*..*
.*...
.*...
输出样例:
Case #1: 2
Case #2: 8思路:
预处出每个点的数字再对0的位置进行搜索,最后对漏网之鱼进行处理
代码:
#include<bits/stdc++.h>
using namespace std;
const int N =310;
int dx[8]={1,1,1,0,0,-1,-1,-1},dy[8]={1,0,-1,1,-1,1,0,-1};
int num[N][N],st[N][N];
char g[N][N]; //记录扫雷整张地图
void bfs(int a,int b,int n) //寻找0点周围的所有点,标记为已遍历
{
st[a][b]=1;
num[a][b]=-1;
for(int i=0;i<8;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x>=0 && x<n && y>=0 && y<n)
{
if(!st[x][y] && num[x][y]!=-1)
{
if(num[x][y]>0) st[x][y]=1,num[x][y]=-1;
if(num[x][y]==0) bfs(x,y,n);
}
}
}
}
int main()
{
int T,n;
scanf("%d",&T);
for(int t=1;t<=T;t++)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%s",g[i]);
memset(num,0,sizeof num);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(g[i][j]!='*') //不是雷的要统计8个点上雷的总个数
{
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0 && x<n && y>=0 && y<n && g[x][y]=='*')
{
num[i][j]++;
}
}
}
else num[i][j]=-1; //如果是雷则标记为-1
}
}
memset(st,0,sizeof st);
int ans=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(num[i][j]==0 && !st[i][j]) //找到一个0点ans++,同时进行bfs
{
ans++;
bfs(i,j,n);
}
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
if(num[i][j]!=-1 && !st[i][j]) ans++; //找到漏网之鱼,每找到一个就ans++
}
printf("Case #%d: %d\n",t,ans);
}
return 0;
}
2、动态网格(Google Kickstart2015 Round D Problem A)
我们有一个 R 行 C 列的矩形网格,其中每个方格内的数字都是 0 或 1。
我们将在网格上执行 N 个操作,每个操作都是以下之一:
- 操作 M:将网格的一个单元格中的数字更改为 0 或 1。
- 操作 Q:确定 1 的不同连通区域的数量。 1 的连通区域是指矩阵内全部为 1 的连通的单元格的子集,在子集区域内通过沿着共享边缘在单元格之间行进,可以从该区域中的任何单元格到达该区域中的任何其他单元格。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含两个整数 R 和 C,表示矩形网格的行数和列数。
接下来 R 行,每行包含一个长度为 C 的由 1 和 0 构成的字符串,表示矩阵网格的初始状态。
接下来一行,包含整数 N,表示操作数量。
接下来 N 行,每行包含一个操作指令,操作指令共两种,如下所示:
M x y z,表示 M 指令,具体含义为将第 x 行第 y 列的方格内的值变为 z。Q,表示 Q 指令,表示进行一次询问。
输出格式
对于每组测试数据,第一行输出 Case #x:,其中 x 为组别编号(从 1 开始)。
接下来 Q 行,每行输出一个询问的结果。
数据范围
1≤T≤10
1≤R,C≤100
0≤x<R
0≤y<C
0≤z≤1
1≤N≤1000
输入样例:
1
4 4
0101
0010
0100
1111
7
Q
M 0 2 1
Q
M 2 2 0
Q
M 2 1 0
Q
输出样例:
Case #1:
4
2
2
2思路:
比较简单的连通块的统计,只是加上了些许操作而已
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1001;
int g[N][N];
int st[N][N];
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int t;
int n,m;
int q;
void bfs(int x,int y)
{
st[x][y]=1;
for(int i=0;i<4;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=0 && ny>=0 && nx<n && ny<m && !st[nx][ny] && g[nx][ny]==1)
{
bfs(nx,ny);
}
}
}
int main()
{
cin>>t;
int cnt=1;
while(t--)
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
string s;
cin>>s;
//cout<<s<<endl;
for(int j=0;j<m;j++)
{
g[i][j]=s[j]-'0';
//cout<<s;
}
}
/*
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cout<<g[i][j];
}
cout<<endl;
}
*/
//cout<<"read";
cin>>q;
cout<<"Case #"<<cnt<<":"<<endl;
cnt++;
while(q--)
{
char op;
cin>>op;
if(op=='Q')
{
//printf("Case #%d:",&cnt);
memset(st,0,sizeof st);
int res=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(g[i][j]==1 && !st[i][j])
{
//cout<<"ko"<<endl;
bfs(i,j);
res++;
}
}
cout<<res<<endl;
}
else
{
int x,y,v;
cin>>x>>y>>v;
g[x][y]=v;
}
}
}
return 0;
}3、走迷宫(模板)
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m)处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8思路:
深搜加距离记录(距离数组d同时作为st数组用)一遍过
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=101;
typedef pair<int,int> PII;
int n,m;
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int g[N][N];
int d[N][N];
int hh,tt;
PII q[N*N];
int bfs()
{
q[tt]={0,0};
d[0][0]=0;
while(hh<=tt)
{
auto t=q[hh++];
int x=t.first;
int y=t.second;
for(int i=0;i<4;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=0 && nx<n && ny>=0 && ny<m && d[nx][ny]==-1 &&g[nx][ny]==0)
{
d[nx][ny]=d[x][y]+1;
//cout<<d[nx][ny]<<endl;
q[++tt]={nx,ny};
}
}
}
return d[n-1][m-1];
}
int main()
{
cin>>n>>m;
memset(d,-1,sizeof d);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
scanf("%d",&g[i][j]);
}
cout<<bfs();
return 0;
}4、画图(第六次CCF计算机软件能力认证)
用 ASCII 字符来画图是一件有趣的事情,并形成了一门被称为 ASCII Art 的艺术。
例如,下图是用 ASCII 字符画出来的 CSPRO 字样。
..____.____..____..____...___..
./.___/.___||.._.\|.._.\./._.\.
|.|...\___.\|.|_).|.|_).|.|.|.|
|.|___.___).|..__/|.._.<|.|_|.|
.\____|____/|_|...|_|.\_\\___/.
本题要求编程实现一个用 ASCII 字符来画图的程序,支持以下两种操作:
- 画线:给出两个端点的坐标,画一条连接这两个端点的线段。简便起见题目保证要画的每条线段都是水平或者竖直的。水平线段用字符
-来画,竖直线段用字符|来画。如果一条水平线段和一条竖直线段在某个位置相交,则相交位置用字符+代替。 - 填充:给出填充的起始位置坐标和需要填充的字符,从起始位置开始,用该字符填充相邻位置,直到遇到画布边缘或已经画好的线段。注意这里的相邻位置只需要考虑上下左右 4 个方向,如下图所示,字符
@只和 4 个字符*相邻。
.*.
*@*
.*.
输入格式
第 1 行有三个整数 m,n 和 q。m 和 n分别表示画布的宽度和高度,以字符为单位。q 表示画图操作的个数。
第 2 行至第 q+1 行,每行是以下两种形式之一:
0 x1 y1 x2 y2:表示画线段的操作,(x1,y1)和 (x2,y2)分别是线段的两端,满足要么 x1=x2 且 y1≠y2,要么 y1=y2 且 x1≠x2。1 x y c:表示填充操作,(x,y) 是起始位置,保证不会落在任何已有的线段上;c 为填充字符,是大小写字母。
画布的左下角是坐标为 (0,0) 的位置,向右为 x 坐标增大的方向,向上为 y 坐标增大的方向。
这 q 个操作按照数据给出的顺序依次执行。画布最初时所有位置都是字符 .(小数点)。
输出格式
输出有 n 行,每行 m 个字符,表示依次执行这 q 个操作后得到的画图结果。
数据范围
2≤m,n≤100
0≤q≤100,
0≤x<m(x 表示输入数据中所有位置的 x 坐标),
0≤y<n(y 表示输入数据中所有位置的 y 坐标)。
输入样例1:
4 2 3
1 0 0 B
0 1 0 2 0
1 0 0 A
输出样例1:
AAAA
A--A
输入样例2:
16 13 9
0 3 1 12 1
0 12 1 12 3
0 12 3 6 3
0 6 3 6 9
0 6 9 12 9
0 12 9 12 11
0 12 11 3 11
0 3 11 3 1
1 4 2 C
输出样例2:
................
...+--------+...
...|CCCCCCCC|...
...|CC+-----+...
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC+-----+...
...|CCCCCCCC|...
...+--------+...
................思路:
我们选择反着读入行列的信息,这样就可以把起点定义为我们熟悉的左上角
洪水覆盖法在这里体现在对封闭图形的填充
代码:
//注意这里的输入是先输入的是列,然后是行
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m ,q;
char g[N][N];
bool st[N][N];
void change(int x1, int y1, int x2, int y2){
if(x1 == x2){// 同一行
for(int i = y1; i <= y2; i ++){
if( g[x1][i] == '|'|| g[x1][i] == '+') g[x1][i]= '+';
else g[x1][i] = '-';
}
}
// 同一列
else if ( y1 == y2){
for(int i = x1; i <= x2; i ++){
if( g[i][y1] == '-' || g[i][y1] == '+') g[i][y1] = '+';
else g[i][y1] = '|';
}
}
}
void paint(int x, int y, char s){
st[x][y] = true;
g[x][y] = s;
int dx[4] = { -1, 0, 1, 0}, dy[4] = { 0, 1, 0, -1};
for(int i = 0; i < 4; i ++){
int a = x + dx[i], b = y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m || st[a][b]) continue;
if(g[a][b] == '|' || g[a][b] == '-' || g[a][b] == '+') continue;
paint(a, b, s);
}
}
int main(){
cin >> m >> n >> q;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
g[i][j] = '.';
while(q --){
int op;
cin >> op;
if(op == 0){
// x和y反着读入
int x1, y1, x2, y2;
cin >> y1 >> x1 >> y2 >> x2;
if(x1 > x2) swap(x1, x2);
if(y1 > y2) swap(y1, y2);
change(x1, y1, x2, y2);
}
else{
int x, y;
char s;
// x和y反着读入
cin >> y >> x >> s;
memset(st, 0, sizeof st);
paint(x, y, s);
}
}
for(int i = n -1; i >= 0; i--){
for(int j = 0; j < m; j++)
cout << g[i][j];
cout << endl;
}
}
5、山峰和山谷(POI2007 & 《信息学奥赛一本通》)
FGD小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。
为了能够对旅程有一个安排,他想知道山峰和山谷的数量。
给定一个地图,为FGD想要旅行的区域,地图被分为 n×n 的网格,每个格子 (i,j) 的高度 w(i,j)是给定的。
若两个格子有公共顶点,那么它们就是相邻的格子,如与 (i,j)相邻的格子有(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)。
我们定义一个格子的集合 S 为山峰(山谷)当且仅当:
- S 的所有格子都有相同的高度。
- S 的所有格子都连通。
- 对于 s 属于 S,与 s 相邻的 s' 不属于 S,都有 ws>ws'(山峰),或者 ws<ws'(山谷)。
- 如果周围不存在相邻区域,则同时将其视为山峰和山谷。
你的任务是,对于给定的地图,求出山峰和山谷的数量,如果所有格子都有相同的高度,那么整个地图即是山峰,又是山谷。
输入格式
第一行包含一个正整数 n,表示地图的大小。
接下来一个 n×n 的矩阵,表示地图上每个格子的高度 w。
输出格式
共一行,包含两个整数,表示山峰和山谷的数量。
数据范围
1≤n≤1000
0≤w≤109
输入样例1:
5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8
输出样例1:
2 1
输入样例2:
5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7
输出样例2:
3 3
样例解释
样例1:

样例2:
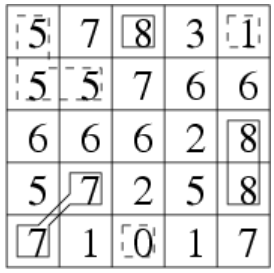
思路:
加两个参数表示有无山峰或者山谷即可,遇到相同的数字就继续bfs,记得bool参数加引用,不然不会改变原来的变量
dfs代码 (超出内存版):
bfs(爆栈)
//dfs超出内存了
#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int g[N][N];
int st[N][N];
int dx[]={-1,1,0,0,1,1,-1,-1};
int dy[]={0,0,-1,1,1,-1,-1,1};//八个方向(新增左上左下右上右下)
int n;
void dfs(int x,int y,bool &h,bool &l)//这里必须引用!
{
st[x][y]=1;
for(int i=0;i<8;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=0 && ny>=0 && nx<n && ny<n)
{
if(g[nx][ny]<g[x][y])l=true;//有比他更低的
else if(g[nx][ny]>g[x][y])h=true;//有比他更高的
else if(g[nx][ny]==g[x][y] && !st[nx][ny])
{
dfs(nx,ny,h,l);
}
}
}
}
int main()
{
cin>>n;
int peak=0,valley=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
scanf("%d",&g[i][j]);
}
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(!st[i][j])
{
bool h=false;
bool l=false;
dfs(i,j,h,l);
if(!h)peak++;//cout<<i<<""<<j<<endl;
if(!l)valley++;//cout<<i<<""<<j<<endl;
}
}
cout<<peak<<" "<<valley;
return 0;
}bfs代码 (AC成功):
#include <iostream>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair <int,int> PII;
const int N = 1010;
int n;
int h[N][N];
bool st[N][N];
void bfs (int sx,int sy,bool &has_higher,bool &has_lower) {
queue <PII> q;
q.push ({sx,sy});
while (!q.empty ()) {
PII t = q.front ();
q.pop ();
for (int i = t.x - 1;i <= t.x + 1;i++) {
for (int j = t.y - 1;j <= t.y + 1;j++) {
if (i < 1 || i > n || j < 1 || j > n) continue;
if (h[i][j] != h[t.x][t.y]) {
if (h[i][j] > h[t.x][t.y]) has_higher = true;
else has_lower = true;
}
else if (!st[i][j]) {
q.push ({i,j});
st[i][j] = true;
}
}
}
}
}
int main () {
cin >> n;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) cin >> h[i][j];
}
int peak = 0,valley = 0;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) {
if (!st[i][j]) {
bool has_higher = false,has_lower = false;
bfs (i,j,has_higher,has_lower);
if (!has_higher) peak++;
if (!has_lower) valley++;
}
}
}
cout << peak << ' ' << valley << endl;
return 0;
}
dfs代码 (AC成功版):
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1010;
int n;
bool f[N][N];
int h[N][N];
// 将两个需要返回的参数,设置为全局变量,则可以正常通过此题。
// 将两个需要返回的参数,设置为带地址符的变量,则MLE
bool has_higher, has_lower;
// 657 ms
void dfs(int sx, int sy) {
f[sx][sy] = true;
for (int x = sx - 1; x <= sx + 1; x++) {
for (int y = sy - 1; y <= sy + 1; y++) {
if (x < 0 || x >= n || y < 0 || y >= n) continue;
if (h[sx][sy] != h[x][y]) { //高度不相等
if (h[sx][sy] < h[x][y]) has_higher = true;
if (h[sx][sy] > h[x][y]) has_lower = true;
} else { //高度相等
if (f[x][y]) continue;
dfs(x, y);
}
}
}
}
int vally, peak;
int main() {
//加快读入
cin.tie(0), ios::sync_with_stdio(false);
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> h[i][j];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (!f[i][j]) {
has_higher = has_lower = false;
dfs(i, j);
if (has_higher && has_lower) continue;
if (has_higher) vally++;
if (has_lower) peak++;
}
}
}
//对于不存在山峰+山谷的一马平地,山峰山谷都输出1
if (peak == 0 && vally == 0) peak = 1, vally = 1;
printf("%d %d\n", peak, vally);
return 0;
}




![[ C++ ] STL---string类的模拟实现](https://img-blog.csdnimg.cn/direct/d0bf4ebbcb8b48d1956915a20441bafc.gif)