491.递增子序列

本题和大家刚做过的 90.子集II 非常像，但又很不一样，很容易掉坑里。

90.子集是可以对数组进行重新排序，再去重。但是这道题是要求子序列，如果对数组重排序会打乱顺序，无法获取子序列。

因此491.递增子序列的去重思路是使用HashSet记录当前层处理过的节点，然后遇到已经处理过的节点直接跳过。（注意这里的跳过用的是continue，因为后面的节点还要继续处理）。

class Solution {
    private List<Integer> path=new LinkedList<>();
    private List<List<Integer>> res=new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    public void backtracking(int[] nums,int startIndex){
        if(path.size()>1) res.add(new ArrayList<>(path));
        Set<Integer> set=new HashSet<>();
        for(int i=startIndex;i<nums.length;i++){
            if(set.contains(nums[i])) continue;
            else if(path.size()==0 || nums[i]>=path.get(path.size()-1)){
                set.add(nums[i]);//当前层的set不要回溯！！！注意这一点
                path.add(nums[i]);
                backtracking(nums,i+1);
                path.remove(path.size()-1);
            }
        }
    }
}

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

46.全排列

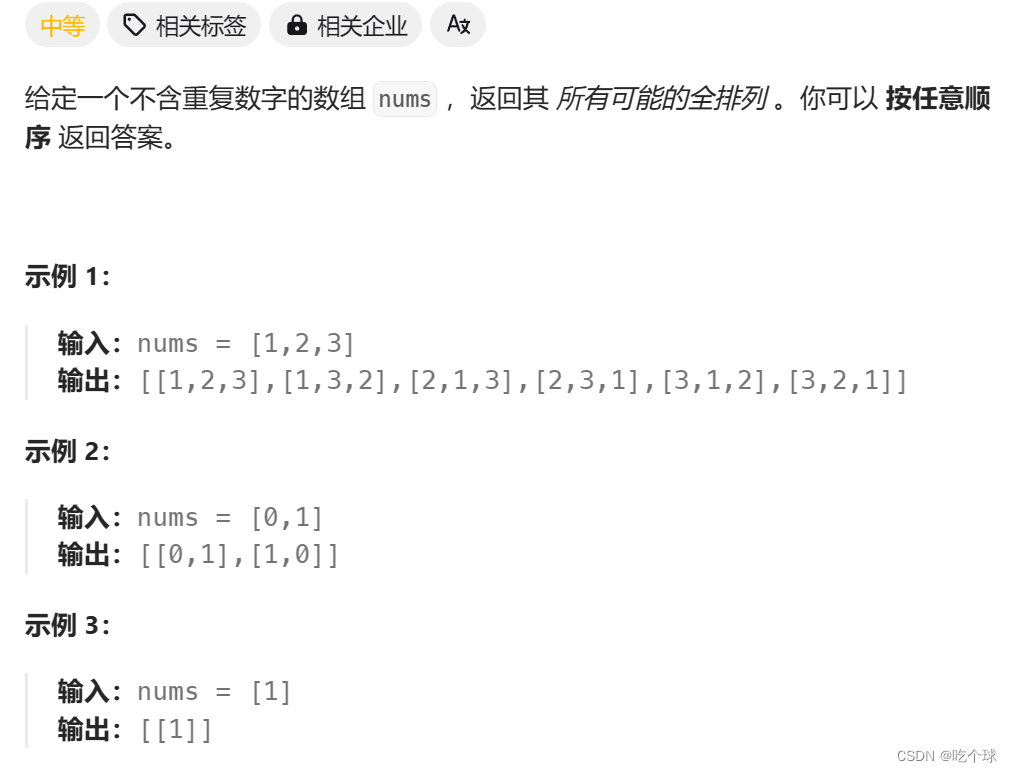
排列问题与组合问题不同的是，组合问题不强调元素的顺序，而排序强调顺序。
思路： 用used数组标记已经使用过的下标，接下来从剩余的元素里取。

class Solution {
    List<Integer> path=new LinkedList<>();
    List<List<Integer>> res=new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        boolean[] used=new boolean[nums.length];//记录当前元素是否已经使用过
        backtracking(nums,used);
        return res;
    }

    public void backtracking(int[] nums,boolean[] used){
        if(path.size()==nums.length){
            res.add(new ArrayList(path));
        }
        for(int i=0;i<nums.length;i++){
            if(used[i]==false){
                used[i]=true;
                path.add(nums[i]);
                backtracking(nums,used);
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}

时间复杂度: O(n!)
空间复杂度: O(n)

47.全排列 II

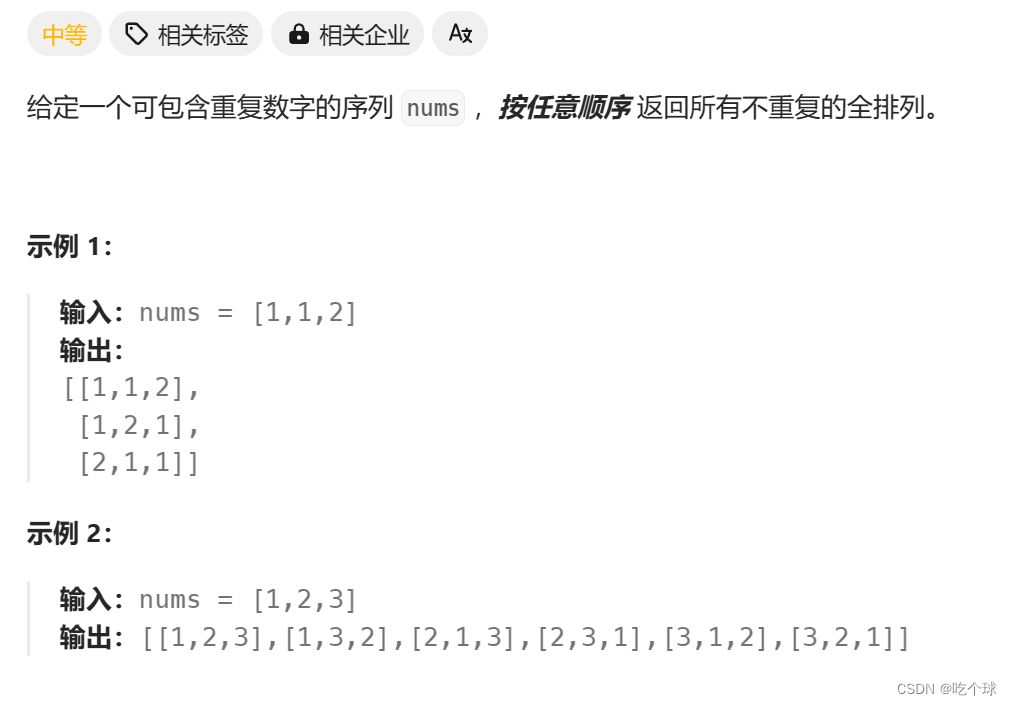
思路： 这道题的去重思想和之前常用的：排序+去重相同。都是在递归函数的for循环里加上去掉同一层遍历到的节点。

class Solution {
    List<Integer> path=new LinkedList<>();
    List<List<Integer>> res=new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used=new boolean[nums.length];//记录当前元素是否已经使用过
        Arrays.sort(nums);//要记得先排序
        backtracking(nums,used);
        return res;
    }
    public void backtracking(int[] nums,boolean[] used){
        if(path.size()==nums.length){
            res.add(new ArrayList(path));
        }
        for(int i=0;i<nums.length;i++){
            if(i>0 && nums[i]==nums[i-1] && used[i-1]==false) continue;//修剪同一层上相同的节点
            if(used[i]==false){
                used[i]=true;
                path.add(nums[i]);
                backtracking(nums,used);
                used[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}

时间复杂度: O(n! * n)
空间复杂度: O(n)