一、飞机降落
问题描述:
N架飞机准备降落到某个只有一条跑道的机场。其中第 i 架飞机在
时刻到达机场上空,到达时它的剩余油料还可以继续盘旋
个单位时间,即它最早可以于 1, 时刻开始降落,最晚可以于
时刻开始降落。降落过程需要
个单位时间。
输入格式:
输入包含多组数据。
第一行包含一个整数N,代表测试数据的组数。
对于每组数据:
第一行包含一个整数T,代表测试数据的组数。
对于每组数据,第一行包含一个整数 N。
接下来的N行,每行包含三个整数。
输出格式:对于每组数据,输出YES或者NO,代表是否可以全部安全降落。
输入样例:
2 3 0 100 10 10 10 10 0 2 20 3 0 10 20 10 10 20 20 10 20
输出样例:
YES NO
思路:
- 首先读取飞机的数量N,然后读取每架飞机的到达时间t、盘旋时间d和降落时间l。
- 使用深度优先搜索(DFS)尝试所有可能的降落顺序。DFS的过程中,我们需要一个bool数组来记录每架飞机的降落状态(例如,是否已经降落)。
bool st[N];// 判断当前飞机是否已经降落- 循环遍历如果当前尝试的飞机不能在剩余油料允许的时间内降落,或者尝试完所有飞机后没有找到合法的降落顺序,则回溯到上一个状态,尝试另一种降落顺序。
- 对于每一架尝试降落的飞机,检查它是否能够在剩余油料允许的时间内开始降落,即降落的开始时间应该在到达时间加盘旋时间的范围内(
上一次降落时间 +
)。
if (p[i].t + p[i].d < time)
// 如果当前时间超过了飞机的最晚降落时间
{
//回溯,回溯到DFS之前的状态。
st[i] = false;
return false;
}
int t = max(time, p[i].t) + p[i].l;// 此次降落时间- 如果当前尝试的飞机可以降落,更新该飞机的状态为已降落,并更新跑道的可用时间为该飞机降落完成的时间。
int t = max(time, p[i].t) + p[i].l;
if (dfs(u + 1, t))
return true;- 如果找到了一个所有飞机都能在其剩余油料允许的时间内完成降落的顺序,则输出"YES",否则输出"NO"。
- 重置st数组,准备下一组数据
for (int i = 0; i < n; i++)
st[i] = false;#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 10 + 20;
struct plane {
ll t,// 到达上空时间
d,// 可盘旋时间
l;// 降落所需时间
}p[N];
bool st[N];// 判断当前飞机是否已经降落
ll n;// 飞机个数。
// u表示已经有U架飞机成功降落了。
// time表示当前的时间,前一架飞机落地的时间。
bool dfs(ll u, ll time)
{
if (u >= n)return true;
// 已经有n架飞机降落,顺序合法
// 遍历所有飞机,考虑它们的降落顺序
for (int i = 0; i < n; i++)
{
if (!st[i])// 如果没有降落
{
st[i] = true;
if (p[i].t + p[i].d < time)
// 如果当前时间超过了飞机的最晚降落时间
{
//回溯,回溯到DFS之前的状态。
st[i] = false;
return false;
}
ll t = max(time, p[i].t) + p[i].l;
if (dfs(u + 1, t))
return true;
//回溯,回溯到DFS之前的状态。
st[i] = false;
}
}
return false;
}
void solve()
{
cin >> n;
for (int i = 0; i < n; i++)// 读入每架飞机的信息
cin >> p[i].t >> p[i].d >> p[i].l;
if (dfs(0, 0))
cout << "YES" << endl;
else
cout << "NO" << endl;
for (int i = 0; i < n; i++)// 重置st数组,准备下一组数据
st[i] = false;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int t = 1;
cin >> t;
while (t--)
solve();
}二、全球变暖
题目描述:
由于全球变暖导致海面上升,科学家预测未来几十年内,岛屿边缘的一个像素范围将会被海水淹没。具体来说,如果一块陆地像素(用“#”表示)与海洋像素(用“.”表示)相邻(即上下左右四个相邻像素中有海洋),这块陆地就会被淹没,变成海洋。给定一个N×N的海域照片,你需要计算根据科学家的预测,照片中会有多少岛屿被完全淹没。
输入描述:
第一行包含一个整数N(1≤N≤1000),表示海域照片的尺寸。
接下来N行,每行包含N个字符,表示海域照片,其中“#”表示陆地,“.”表示海洋。照片保证第一行、第一列、第N行、第N列的像素都是海洋。输出描述:
输出一个整数,表示根据科学家的预测,会有多少岛屿被完全淹没。
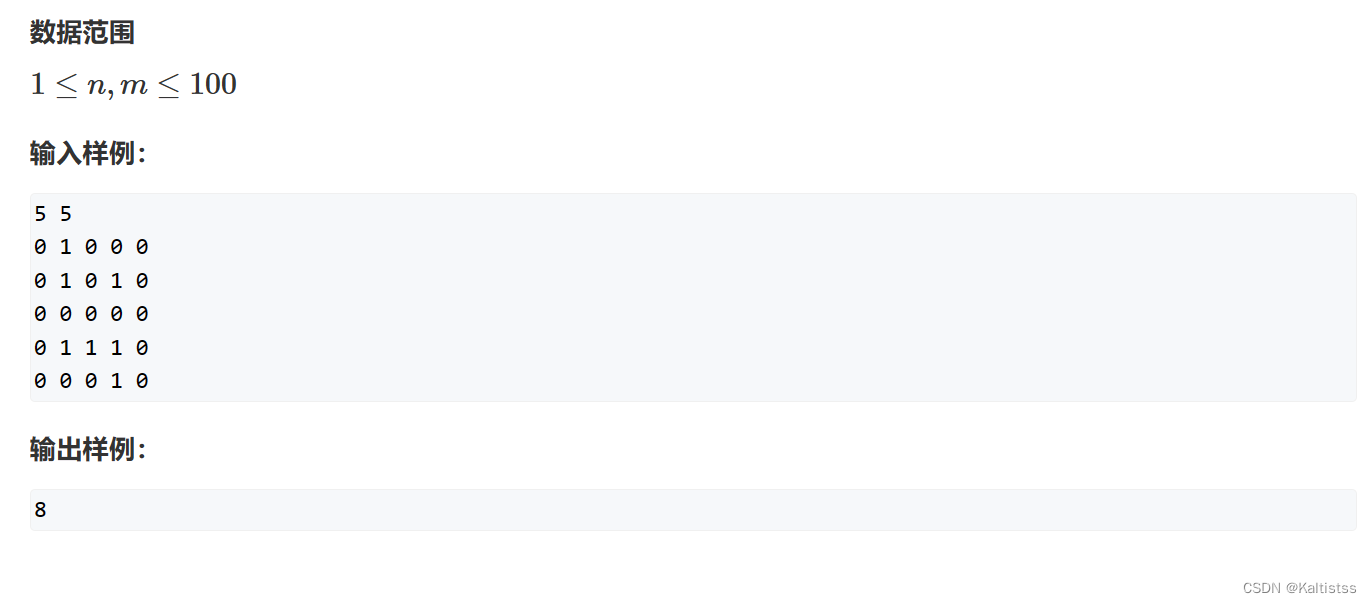
样例输入:
7
..##...
.###...
.#..#..
..####.
...#.#.
....###
.......样例输出:
1
解释:
给定的海域照片中有两座岛屿,分别由"#"字符组成。根据科学家的预测,只有左边的岛屿会被完全淹没,因此输出为1。
思路:
初始化和输入
- 定义了一个二维数组
mp来存储给定的海域照片,其中“#”表示陆地,“.”表示海洋。 col数组用于记录每个像素点属于哪一个岛屿。vis数组用于标记一个岛屿是否会被完全淹没。- 输入尺寸
n和海域照片。
using ll = long long;
const int N = 1e3 + 5;
int n, scc, // 尺寸和颜色编号
col[N][N];// 用于记录每个像素点属于哪一个岛屿
char mp[N][N];// 存储海域照片
// 表示四个可能的移动方向:上,下,左,右
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool vis[N * N];// 用于标记一个岛屿是否被完全淹没-
确定岛屿
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
// 遍历每一个像素点
{
if (col[i][j] || mp[i][j] == '.') continue;
scc++; dfs(i, j);
// 岛屿数量++ 开始DFS搜索
}首先,我们需要识别地图上所有的岛屿。这可以通过遍历整个照片来完成,每当我们遇到一个“#”(陆地)字符,我们就从这个点开始进行深度优先搜索(DFS),以找出这块陆地连接的所有部分,即一个完整的岛屿。在搜索过程中,我们将不同的岛屿染上不同的颜色,并将访问过的陆地标记为已访问,以避免重复计算。
-
DFS搜索判断岛屿是否会被淹没
对于每个岛屿,我们需要判断它是否会被完全淹没。这意味着我们需要检查岛屿的边缘是否与海洋相邻。如果岛屿的任何一部分位于边缘(即,与地图边缘的海洋相邻)或者有至少一个部分的上下左右四个方向中有一个是海洋,则这个岛屿将不会被完全淹没。否则,该岛屿将被视为会被完全淹没。
// 找出岛屿的范围
void dfs(int x, int y)
{
col[x][y] = scc;// 标记该像素点属于当前岛屿
for (int i = 0; i < 4; i++)
// 遍历所有可能的移动方向
{
int nx = x + dx[i], ny = y + dy[i];// 计算新的位置
if (col[nx][ny] || mp[nx][ny] == '.') continue;
// 如果是访问过或者是海洋则跳过
dfs(nx, ny);
}
}- 使用
dfs函数来找出每一个岛屿的范围。dfs函数通过递归地搜索每个陆地像素的上下左右四个相邻位置来实现,如果相邻位置也是陆地(“#”),则继续进行DFS搜索。 - 在
dfs的过程中,使用col数组来标记当前正在搜索的岛屿的所有像素点,即将这些点都标记为当前岛屿的编号scc。 - 通过
dx和dy数组来表示四个可能的移动方向(上、下、左、右),以便在DFS搜索中移动到相邻的像素点。
for (int k = 0; k < 4; ++k)
// 遍历四个方向
{
int x = i + dx[k], y = j + dy[k];
if (mp[x][y] == '.') tag = false;
// (x, y)处的像素是否被海洋淹没(全是陆地就不淹没)
}
-
计算被淹没的岛屿数量
- 使用
tag标记来表示当前检查的像素点是否会被淹没,即如果四个方向中有海洋,则tag为false,表示该岛屿的这个部分会被淹没。 - 对于每一个岛屿,如果其任何一个部分不会被淹没,则整个岛屿都不会被淹没。使用
vis数组来标记这些情况。如果vis数组中对应的岛屿编号为false,则将其标记为true并增加ans计数器(记录不会被淹没的岛屿数量)。
if (tag)// 如果四个方向都不是海洋,则当前陆地像素点不会被淹没
{
if (!vis[col[i][j]]) ans++;
// 如果这个岛屿还没有被计入被淹没的岛屿中, 完全被淹没的岛屿++
vis[col[i][j]] = true;// 标记这个岛屿为被淹没
}- 最后,输出
scc - ans,即总岛屿数量减去不会被淹没的岛屿数量,得到的就是会被完全淹没的岛屿数量。
cout << scc - ans << '\n';#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 5;
int n, scc, // 尺寸和颜色编号
col[N][N];// 用于记录每个像素点属于哪一个岛屿
char mp[N][N];// 存储海域照片
// 表示四个可能的移动方向:上,下,左,右
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool vis[N * N];// 用于标记一个岛屿是否被完全淹没
// 找出岛屿的范围
void dfs(int x, int y)
{
col[x][y] = scc;// 标记该像素点属于当前岛屿
for (int i = 0; i < 4; i++)
// 遍历所有可能的移动方向
{
int nx = x + dx[i], ny = y + dy[i];// 计算新的位置
if (col[nx][ny] || mp[nx][ny] == '.') continue;
// 如果是访问过或者是海洋则跳过
dfs(nx, ny);
}
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;//读入尺寸
for (int i = 1; i <= n; i++)
cin >> mp[i] + 1;// 读入海域照片数据
// 从这一行的第二个元素开始读取输入
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
// 遍历每一个像素点
{
if (col[i][j] || mp[i][j] == '.') continue;
scc++; dfs(i, j);
// 岛屿数量++ 开始DFS搜索
}
int ans = 0;// 用于记录被完全淹没的岛屿数量
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
if (mp[i][j] == '.') continue;
// 如果是海洋,则跳过
bool tag = true;// 标记是否会被淹没
for (int k = 0; k < 4; ++k)
// 遍历四个方向
{
int x = i + dx[k], y = j + dy[k];
if (mp[x][y] == '.') tag = false;
// (x, y)处的像素是否被海洋淹没(全是陆地就不淹没)
}
if (tag)// 如果四个方向都不是海洋,则当前陆地像素点不会被淹没
{
if (!vis[col[i][j]]) ans++;
// 如果这个岛屿还没有被计入被淹没的岛屿中, 完全被淹没的岛屿++
vis[col[i][j]] = true;// 标记这个岛屿为被淹没
}
}
cout << scc - ans << '\n';// 输出未被淹没的岛屿数量
return 0;
}三、军训排队
问题描述
数字王国开学了,它们也和我们人类一样有开学前的军训。现在一共有n名学生,每个学生有一个自己的名字(在数字王国里,名字就是一个正整数)。注意,学生们可能出现重名的情况。叛逆教官来看了之后感觉十分别扭,决定将学生重新分队。排队规则为:将学生分成若干队,每队里面至少有一个学生,且每队里面学生的名字不能出现倍数关系(注意,名字相同也算是倍数关系)。现在请你帮忙算算最少可以分成几队?
例如:有4名学生(2,3,4,4),最少可以分成(2,3)、(4)、(4)共3队。
输入格式
第一行包含一个正整数n,表示学生数量。
第二行包含n个由空格隔开的整数,第i个整数表示第i个学生的名字α。
输出格式
输出共1行,包含一个整数,表示最少可以分成几队。
样例输入
4
2 3 4 4
样例输出
3
(解释:如上所述,可以将4名学生分成(2,3)、(4)、(4)共3队,满足每队学生的名字之间不存在倍数关系。)
思路:
枚举最少队伍数量:
首先,我们可以从小到大枚举“最少队伍的数量”。这意味着,我们从最少的队伍数开始尝试,逐渐增加队伍数,直到找到一个可行的分组方案。
搜索合法性:
对于每一个枚举的队伍数量,我们需要判断在这个数量下是否可以成功分组。这可以通过搜索来实现。具体来说,我们确定总队伍数量后,对于每一个人(或元素),枚举他所属的队伍。这里,回溯法是一种非常有效的搜索技术。
剪枝策略:
在搜索过程中,为了提高效率,我们需要采用剪枝策略。一种常见的剪枝方法是,当某个人(或元素)尝试加入某个队伍时,我们立即检查这个队伍中是否已存在与该人具有某种特定关系(如倍系关系)的其他成员。如果存在这样的关系,我们就可以直接跳过当前尝试,因为它不可能导致一个有效的分组。
#include<bits/stdc++.h>
using namespace std;
const int N = 15; // 最大可能的队伍数目或学生数
int a[N], n; // a数组用来存储每个学生的名字,n表示学生的数量
vector<int>v[N]; // 使用vector数组来表示每个队伍,存储队伍中学生的名字
// dfs函数尝试将学生分配到不同的队伍中
bool dfs(int cnt, int dep) {
// cnt表示当前尝试的队伍数量,dep表示当前处理到第几个学生
if (dep == n + 1) {
// 如果dep等于n+1,说明所有学生都已经被分配到队伍中
return true;
}
for (int i = 1; i <= cnt; ++i) {
// 遍历当前所有队伍,尝试将学生放入
bool tag = true; // 用tag标记当前学生是否能放入队伍i中
for (const auto& j : v[i]) {
// 遍历队伍i中已经有的学生名字
if (a[dep] % j == 0) {
// 如果当前学生的名字是队伍中某学生名字的倍数
tag = false; // 不能放入这个队伍
break; // 停止遍历队伍
}
}
if (!tag) continue; // 如果不能放入当前队伍,继续尝试下一个队伍
v[i].push_back(a[dep]); // 将学生放入队伍i
if (dfs(cnt, dep + 1)) return true; // 递归地尝试放置下一个学生
v[i].pop_back(); // 如果不能成功放置,将学生从队伍i中移除
}
return false; // 如果所有队伍都不能放入当前学生,返回false
}
int main() {
// 设置输入输出流以提高效率
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n; // 读入学生数量
for (int i = 1; i <= n; i++) {
cin >> a[i]; // 读入每个学生的名字
}
for (int i = 1; i <= n; i++) {
// 从1个队伍尝试到n个队伍,找到最少可以分成的队伍数量
if (dfs(i, 1)) {
// 如果可以将所有学生分配到i个队伍中
cout << i << '\n'; // 输出队伍的数量
break;
}
}
return 0;
}
今天就先到这了!!!

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。